Контрольна робота
З дисципліни: “Логіка”
Зміст
Завдання
Теоретичне питання
Простий категоричний силогізм
Практичні завдання
Список літератури
Завдання контрольної роботи
ВАРІАНТ 1
Теоретичне питання:
Простий категоричний силогізм.
Задачі:
1. Доберіть поняття, відношення між якими можна зобразити у колах Ейлера таким чином:
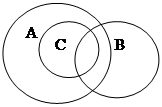 |
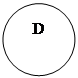
2. Здійсніть обмеження та узагальнення таких понять: троянда, крадіжка, фінансист Васюта.
3. Визначте, чи правильно здійснено логічний поділ, і укажіть вид поділу: спектакль складався з двох актів; злочинці поділяються на повнолітніх та неповнолітніх; вищі навчальні заклади поділяються на університети та інститути.
4. Застосовуючи правила "логічного квадрату", установіть істинність суджень Е, О, А, якщо істинним є судження:
Деякі науки є простими.
5. Формалізуйте судження і складіть для нього таблицю істинності:
Н. і К. матимуть достатні аргументи для обґрунтування свого проекту, якщо вони проведуть відповідні консультації або залучать до співпраці досвідченого у цій галузі спеціаліста.
6. Зробіть безпосередні умовиводи засобом обернення, перетворення і протиставлення предиката з такого засновку:
Деякі слідчі не є юристами.
7. Визначте фігуру й модус силогізму і поясніть результат: Іванченко має право на відпочинок, так як він є громадянином України, а всі громадяни України мають право на відпочинок.
8. Наведіть приклад використання індуктивного методу єдиної схожості із практики роботи фірми.
9. Доведіть прямим методом тезу: Деякі з вулиць м. Сум знаходяться в аварійному стані.
1. Простий категоричний силогізм
Уперше систематичний розгляд теорії висновку дає Арістотель в «Аналітиках», вона отримала назву «силогістика».
Категоричним силогізмом називають дедуктивний умовивід, який складається із двох засновків і висновку, представлених судженнями виду: ASP, ESP, ISP, OSP.
Іншими словами, простий категоричний силогізм — це такий дедуктивний умовивід, в якому висновок здійснюється із двох категоричних суджень на основі співвідношення дескриптивних термінів.
Наприклад:
1. 2. |
Будь-який умовивід (М) породжує нове знання (Р). Оскільки категоричний силогізм (S) належить до класу умовиводів (М), то |
| Отже, він (S) породжує нове знання (Р). |
Аналізуючи наведений приклад категоричного силогізму, стає очевидним, що він за структурою складається із трьох термінів: S, М, Р.
Термін, що входить до висновку як його суб'єкт, називається меншим і позначається буквою S.
Термін, який виконує роль предиката висновку, називається більшим і позначається буквою Р.
Більший і менший терміни називаються крайніми.
Термін, що входить в обидва засновки, але відсутній у висновку, називається середнім і позначається буквою М.
Відповідно до назви термінів засновок, до якого входить більший термін, називається більшим.
Засновок, до якого входить менший термін, називається меншим.
У нашому прикладі більший засновок 1, а менший — 2. Виходячи із зазначеного, структуру силогізму можна записати у вигляді імплікації, де антецедентом буде кон'юнкція засновків, а консеквентом — висновок:
[А (М Р) Λ А (S M)] ![]() A(S P).
A(S P).
![]()
![]() Якщо розглядати структуру силогізму в залежності від розташування трьох термінів, то можливі чотирисхеми:
Якщо розглядати структуру силогізму в залежності від розташування трьох термінів, то можливі чотирисхеми:
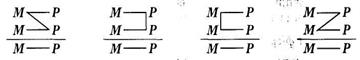
Ці схеми називають фігурами категоричного силогізму, тобто різновидами категоричного силогізму, які визначаються розташуванням середнього терміна.
Різновиди категоричного силогізму розрізняють за формами засновків і висновку. їх прийнято називати модусами категоричного силогізму.
При побудові категоричного силогізму дотримуються певних правил, які поділяються на:
а) загальні правила категоричного силогізму і
б) спеціальні правила фігур.
До загальних правил категоричного силогізму відносяться такі:
1. У простому категоричному силогізмі повинно бути лише три терміни.
2. Середній термін повинен бути розподіленим хоча б в одному з засновків.
3. Якщо крайній термін розподілений (або не розподілений) у засновку, то він повинен бути розподіленим (або нерозподіленим) у висновку.
4. ![]() Якщо один із засновків заперечувальне судження, то і висновок буде заперечувальним судженням.
Якщо один із засновків заперечувальне судження, то і висновок буде заперечувальним судженням.
5. Якщо один із засновків часткове судження, то і висновок буде частковим судженням.
6. Із двох заперечувальних суджень висновок отримати не можливо.
7. Із двох часткових суджень висновок отримати неможливо.
Спеціальні правила фігур
Перша фігура:
1. Більший засновок — судження загальне.
2. Менший засновок — судження стверджувальне.
Друга фігура:
1. Більший засновок повинен бути загальним судженням.
2. Один із засновків — заперечувальне судження.
Третя фігура:
1. Менший засновок — стверджувальне судження.
2. Висновок — часткове судження.
Четверта фігура:
1. Якщо більший засновок — стверджувальне судження,
то менший повинен бути загальним судженням.
2. Якщо один із засновків — заперечувальне судження,
то більший засновок повинен бути загальним судженням.
Побудуємо доведення спеціальних правил.
Спеціальні правила фігур виводяться із загальних, а також із знання про розташування середнього терміна в засновках. Прикладом може служити доведення правил першої фігури.
Припустимо, що правила першої фігури неправильні, а правильні їх заперечення:
1. Більший засновок повинен бути частковим судженням.
2. Менший — заперечувальним судженням.
Якщо у результаті доведення цього припущення прийдемо до суперечності, то наше припущення відпаде як хибне, а істинним визнається твердження, що складає правила першої фігури.
Доведення:
- якщо приймаємо наше припущення, то висновком у силогізмі за першою фігурою буде заперечувальне судження (4 — загальне правило силогізму: скорочено — ЗПС);
- окрім цього, висновок буде частково-заперечувальним судженням OSP (по 5 — ЗСП);
- у заперечувальному судженні Р — розподілений;
- отже, більший термін буде розподілений і у засновку (З — ЗСП);
- оскільки більший і менший засновки заперечувальні, то висновок отримати неможливо (6 — ЗПС).
Таким чином, наше припущення неправильне і воно відпадає. Тоді коректними будуть названі правила першої фігури. Таким способом доводять правила решти трьох фігур.
Використовуючи ЗПС і спеціальні правила фігур, для кожної фігури можна вивести усі правильні модуси. У межах кожної фігури можливі 16 комбінацій засновків від чотрирьох видів суджень ASP, ESP, ISP, OSP:
| AA | EA | IA | OA |
| AE | EE | IE | OE |
| AI | EІ | II | ОІ |
| AO | EO | 10 | ОО |
Перше правило виключає повністю комбінації 3 і 4 колонок. Варіанти 2 і 4 першої колонки суперечать першому правилу фігури.
Варіанти 2 і 4 другої колонки виключаються з розгляду за 6 — ЗПС.
Отже, залишаються комбінації АА, AI, EA, EI, із яких отримують модуси ААА, AІІ, EAE, ЕІО. Кожний модус має конкретне ім'я, що використовується як певний мнемонічний засіб: Barbara, Celarent, Darii, Ferio1.
Таким же чином можна вивести правильні модуси II, III, IV фігур. Із чотирьох фігур перша вважається найдосконалішою. Це зумовлено такими обставинами:
По-перше, тільки ця фігура дає у висновку всі чотири типи категоричних суджень.
Відповідні назви мають модуси II, III фігур: модуси II фігури — Cesare, Camestres, Festino, Baroco; модуси III фігури — Darapti, Disamis, Datisi, Felap-ton, Bocardo, Ferison; модуси ІУ фігури — Bramantip, Camenes, Dimaris, Fesapo, Fresison.
По-друге, в першій фігурі частковий випадок підводиться під загальне положення.
По-третє, тільки ця фігура дає у висновку висловлювання ASP, мовою якого формулюються закони науки.
Зважаючи на це, модуси першої фігури приймаються як основні, а модуси решти трьох фігур як похідні, які можна вивести із основних.
Спочатку обгрунтуємо коректність модусів першої фігури, а потім перейдемо до виведення модусів II, III, IV фігур.
Логічна коректність модусів першої фігури випливає із умов істинності суджень ASP, ESP, ISP, OSP.
Візьмемо модус А А А.
Спочатку припустимо, що засновки AMP і ASM — істинні, а висновок — ASP — хибний. Потім, відповідно до умови істинності загальностверджувального судження: якщо ASP — хибне, то у множині S знайдеться хоча б один індивід а, який не належить множині Р. Але за угодою, якщо ASM — істинне, то будь-який індивід множини S належить множині М (навіть і а). Однак, одночасна приналежність а до класу М і не приналежність до класу Р виключається в силу угоди про істинність засновку AMP. Тобто, все, що належить М (а М належить і індивід а), належить і Р. Таким чином, наше припущення про істинність AMP і ASM та хибність висновку ASP приводить до суперечності, чим і встановлюється логічна коректність модусу ААА.
Обгрунтуємо модус ЕАЕ.
Знову припускаємо, що засновки ЕМР і ASM — істинні, а висновок ESP — хибний. Якщо ESP — хибне, то за умовою істинності загальнозапечувального судження існує хоча б один індивід а множини S, який належить множині Р. За припущенням висновок ASM — істинний, отже, кожен індивід із S, в тому числі і а, належить М. Але приналежність предмета а множині Р і множині М виключається припущенням про істинність засновку ЕМР. Виходить, що припущення про істинність ЕМР і ASM та хибність ESP спростоване і цим самим визнається логічна коректність модусу ЕАЕ.
Обгрунтуємо коректність третього модусу першої фігури AІІ.
Припустимо, що засновки AMP і ISM — істинні, а висновок ISP — хибний. Відповідно до умов істинності частковостверджувального судження, якщо засновок ISM — істинний, то існує, в крайньому разі, один індивід а множини S, який належить і множині М. У той же час за умови хибності висновку ISP не існує жодного індивіда множини S, у тому числі й індивіда а, який би не належав множині Р. Належність а множині М і неналежність а множині Р суперечить припущенню про істинність засновку AMP. Адже AMP істинне, якщо всі елементи множини М (в тому числі і а) належать множині Р. Отже, припущення про істинність засновків AMP і ISM та хибність висновку ISP відпадає. Цим самим стверджується логічна коректність модусу AІІ.
Нарешті побудуємо доведення для четвертного модусу першої фігури ЕІО.
Нехай засновки ЕМР і ISM — істинні, а висновок OSP — хибний. За умови істинності частковостверджувального судження ISM істинне, коли, у крайньому разі, існує хоча б один індивід а множини S, який належить М. Висновок OSP хибний (за умов істинності частковозаперечувального судження), коли всі індивіди множини S, в тому числі і а, який належить М, належать Р. Однак, належність індивіда а множині М і множині Р суперечить умовам істинності загальнозаперечувального судження, яким представлений більший засновок і який, згідно з припущенням, є істинним. Отже, припущення про істинність засновків ЕМР і ISM та хибність висновку OSP спростовується і цим доводиться логічна коректність модусу АІО.
Таким чином, використовуючи умови істинності ASP, ESP, ISP та OSP, обґрунтовують логічну коректність модусів першої фігури.
Логічна коректність модусів П, Ш та ІУ фігур встановлюється за допомогою модусів першої фігури та відповідних правил висновку.
Йдеться про такі правила:
1. ASP |= ISP правила висновку, що засновані на відношенні
ESP |= OSP підпорядкування.
2. OSP |= ┐ АSP правила висновку, що засновані на відношенні
ISP |= ┐ ESP суперечності.
3. ASP |= IPS правила обернення.
ISP |= IPS
ESP |= EPS.
Зауважимо, що назви модусів (особливо П, Ш, та ІУ фігур) виконують не тільки мнемонічну функцію. Початкові букви В, С, D, F вказують на ті модуси першої фігури, які отримують в результаті зведення. Голосні вказують на кількісну і якісну характеристики засновків та висновку конкретного модусу, а приголосні — на спосіб його обгрунтування:
- буква s показує, що судження, яке позначене голосною, після якої стоїть ця буква, повинно піддаватися чистому оберненню;
- буква р означає, що судження, яке позначене голосною, після якої стоїть ця буква, повинне піддаватися оберненню з обмеженням;
- буква т вказує на заміну місцями засновків;
- буква с вказує, що даний модус може бути зведеним до модусу першої фігури шляхому непрямого доведення.
Візьмемо модус «Cesare». Буква С вказує на те, що його можна звести до модусу «Celarent». Буква s вимагає при зведенні обернути більший засновок без обмеження:
| ЕРМ | 1. | |
| ASM | 2. | ASM |
| 3. | EMP | — правило «S», 1 |
| 4. | ESM | — правило І фігури, 3, 2. |
Побудуємо доведення модусу «Вагосо», де приголосна с вказує на необхідність скористатися непрямим доведенням.
| АРМ | 1. | АРМ | |
| OSM | 2. | OSM | |
| OSP | 3. | ASP | — припущення |
| 4. | ASM | — правило І фігури, 1, 3 | |
| 5. | OSP | — ВЗ, 2, 4. |
Наведені доведення модусів свідчать про те, що зазначений вище список правил висновку достатній для обгрунтування логічної коректності будь-якого модусу ІІ, III та IV фігур.
Практичні завдання
Задача 1
Доберіть поняття, відношення між якими можна зобразити у колах Ейлера таким чином:
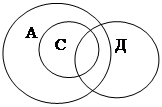 |
Відповідь:
А – викладач
В – державний службовець
С – кандидат наук
Д – альпініст
Задача 2
Здійсніть обмеження та узагальнення таких понять: троянда, крадіжка, фінансист Васюта.
Відповідь:
| Поняття: | троянда | крадіжка | фінансист Васюта. |
| Узагальнення: | троянда – квітка | крадіжка – злочин | фінансист Васюта – бізнесмен |
| Обмеження: | троянда – червона | крадіжка – коштів | фінансист Васюта – керуючий банку „Топаз” |
Задача 3
Визначте, чи правильно здійснено логічний поділ, і укажіть вид поділу: спектакль складався з двох актів; злочинці поділяються на повнолітніх та неповнолітніх; вищі навчальні заклади поділяються на університети та інститути.
Відповідь:
1) „спектакль складався з двох актів” – поділ поняття не відбулося, тому що окремий акт не є спектаклем, а є поділ предмета на частини
2) „злочинці поділяються на повнолітніх та неповнолітніх” – поділ поняття правильний, вид поділу – дихотомічний. Тому, що діє формула
а
А![]()
не а
тобто, якщо злочинець повнолітній, то він не може бутити неповнолітнім. Ознака віку людини охоплює все життя людини
3) Поділ неправильний, тому що не охоплює інших видів родового поняття „ВНЗ”, тобто це неповний поділ. Наприклад, є ще академія.
Задача 4
Застосовуючи правила "логічного квадрату", установіть істинність суджень Е, О, А, якщо істинним є судження:
Деякі науки є простими.
Відповідь:
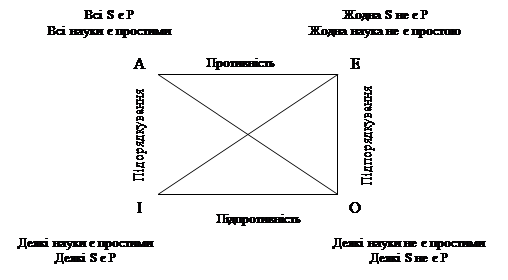
За правилом „логічного квадрату”:
- якщо істинне (згідно завдання) судження І, то по відношенню заперечення судження Е обов`язково хибне;
- оскільки судження І та О охоплюють весь зміст предикату і судження І істинне, то по відношенню під противності судження О теж істинне;
- істинність судження О по відношенню суперечності доводить хибність судження А.
Задача 5
Формалізуйте судження і складіть для нього таблицю істинності:
Н. і К. матимуть достатні аргументи для обґрунтування свого проекту, якщо вони проведуть відповідні консультації або залучать до співпраці досвідченого у цій галузі спеціаліста.
Відповідь:
(АvВ) → С це імплікативне розподільно-виключаюче судження
Таблиця істинності
| А | В | А U В | С | (А U В)→С |
| і | і | х | і | х |
| і | х | і | і | і |
| х | і | і | х | х |
| х | х | х | х | і |
А – „або проведуть відповідні консультації”
В – „або залучать до співпраці досвідченого у цій галузі спеціаліста”
Просте судження А – хибне, просте судження В – істинне, значить А U В
– істинне.
Задача 6
Зробіть безпосередні умовиводи засобом обернення, перетворення і протиставлення предиката з такого засновку:
Деякі слідчі не є юристами.
Відповідь:
Засіб протиставлення:
![]()
Засіб обернення:
![]()
Деякі слідчі не є юристами, отже, жоден юрист не є неслідчім.
Задача 7
Визначте фігуру й модус силогізму і поясніть результат: Іванченко має право на відпочинок, так як він є громадянином України, а всі громадяни України мають право на відпочинок.
Відповідь:
Структура наведеного силогізму – перша фігура силогізму:
![]()
М – громадянин України, S – Іванченко, Р – право на відпочинок.
Менший термін – С
Більший термін – Р
Середній термін – М
Графічно перша фігура силогізму відображається так:
![]() M _____________ P
M _____________ P
![]() S_____________ M
S_____________ M
Модус даної першої фігури: А І І, тому що
Більший термін – судження загальноствердне (А),
Менший термін – судження частковоствердне (І),
Отже, висновок – судження частковоствердне (І).
Модус даної першої фігури: А А А,
Обидва засновники – загальностверджені (А), тому загально стверджений і висновок (А).
Задача 8
Наведіть приклад використання індуктивного методу єдиної схожості із практики роботи фірми.
Відповідь:
В відділенні зв`язку „Укртелеком” встановлено три випадки вчинення крадіжки однаковим способом (цінності виймалися із страхових мішків без їхнього пошкодження): 1 лютого, 10 і 15 травня. Слідство встановило, що у всіх трьох випадках пошту перевозив до поштамту експедитор Іванов. Відправляли і отримували пошту в усіх трьох випадках різні працівники пошти: 1 лютого – Шевчук і Сорока, 10 травня – Мороз і Литвин, 15 травня – Тарасюк і Петрук. На цій підставі слідчий зробив висновок про версію, що крадіжка скоєна експедитором Івановим.
У вигляді схеми цей умовивід можна записати так:
| Випадки | Коло осіб, що мали відношення до відправки, перевезення та приймання пошти | Явище, яке спостерігається |
| 1 лютого | Іванов, Шевчук і Сорока | крадіжка |
| 10 травня | Іванов, Мороз і Литвин | крадіжка |
| 15 травня | Іванов, Тарасюк і Петрук | крадіжка |
| Отже, крадіжка скоєна Івановим | ||
Задача 9
Доведіть прямим методом тезу: Деякі з вулиць м. Сум знаходяться в аварійному стані.
Відповідь:
Судження 1. Будь-яка з вулиць м. Сум може знаходитись в аварійному стані – істинне судження.
Судження 2. Всі вулиці знаходяться в місті Суми – істинне судження.
Судження 3. аварійний стан – це положення, коли вулиця не виконує призначені їй функції – істинне судження.
Судження 4. В місті Суми є вулиці, які не виконують призначені їм функції – істинне судження.
Отже, деякі з вулиць міста Суми знаходяться в аварійному стані.
Отже, деякі з вулиць міста Суми знаходяться в аварійному стані.
Список літератури
1. Арутюнов В.Х., Мішин В.М., Кирик Д.П. Логіка. – К.: КНЕУ, 2000.
2. Волошко І.М., Семенов І.С. Практикум з логіки. – К.: Вид-во Київського ун-ту, 1993.
3. Жеребкін В.Є. Логіка. – Х.: Основа, 1998.
4. Ивлев Ю.В. Логика: Сборник упражнений. – М.: Книжный дом «Университет», 1999.
5. Ішмуратов А.Т. Вступ до філософської логіки. – К.: Абрис, 1997.
6. Кириллов В.Н., Орлов Г.А. Упражнения по логике. – М.: МЦУПЛ, 1999.
7. Кириллов В.Н., Старченко А.А. Логика. – М.: Юрист, 1999.
8. Кондаков Н.Н. Логический словарь. – М.: Сов. энциклопедия, 1990.
9. Орендарчук Г.О. Основи логіки. – Тернопіль: СМП “Астон”, 2001.
10. Рузавин Г.Н. Логика. – М.: ЮНИТИ, 2002.
11. Упражнения по логике: Учебное пособие. – М.: Юрист, 1993.
12. Хоменко І.В. Логіка в задачах. – К.: Четверта хвиля, 1998.
13. Хоменко І.В., Алексюк І.А.
10-09-2015, 21:47
