Задание 1.4
Максимизация прибыли универмага
Большой универсальный магазин собирается заказать новую коллекцию костюмов для весеннего сезона. Решено заказать 4 типа костюмов. Три типа – костюмы широкого потребления (из полиэстеровых смесей, шерстяные, хлопковые). Четвертый тип – дорогие импортные модельные костюмы из различных тканей. Имеющийся у менеджеров магазина опыт и специальные исследования позволяют оценить средние затраты рабочего времени продавцов на продажу одного костюма каждого типа, объём затрат на рекламу и площади в расчете на один костюм каждого типа. Все эти данные, а также прибыль от продажи одного костюма представлены в таблице.
| Тип костюма | Прибыль, дол | Время, час. | Реклама, у.е. | Площадь, м2 |
| Полиэстер | 35 | 0,4 | 2 | 1,00 |
| Шерсть | 47 | 0,5 | 4 | 1,50 |
| Хлопок | 30 | 0,3 | 3 | 1,25 |
| Эластик | 90 | 1,0 | 9 | 3,00 |
Предполагается, что весенний сезон будет длиться 90 дней. Магазин открыт 10 часов в день, 7 дней в неделю. Два продавца постоянно будут в отделе костюмов. Выделенная отделу костюмов площадь составляет прямоугольник 100 ´ 60 м2 . Бюджет, выделенный на рекламу всех костюмов на весенний сезон, составляет 15000 у. е.
1. Сколько костюмов каждого типа надо закупить, чтобы максимизировать прибыль?
2. Допустим, что менеджмент магазина считает необходимым закупить не менее 200 костюмов каждого типа. Как это требование повлияет на прибыль магазина?
При ответе на следующие вопросы сохраните ограничение (2).
3. Изменится ли оптимальное решение, если прибыль от продажи одного полиэстерового костюма переоценена (недооценена) на 1 у. е, на 2 у. е?
4. Обоснуйте, будет ли каждое из предлагаемых решений полезно для магазина:
отдать в распоряжение отдела костюмов 400 м2 от отдела женской спортивной одежды. Предполагается, что на этой площади магазин может получить прибыль всего лишь 750 у.е. за последующие 90 дней;
истратить дополнительно 400 у.е. на рекламу.
5. Если общее число закупленных костюмов не может превысить 5000 шт., то как такое ограничение повлияет на оптимальное решение?
Решение задачи 1.4
Обозначим через Х1 – количество костюмов из полиэстеровых смесей, Х2 – количество костюмов из шерсти, Х3 – количество костюмов из хлопка и Х4 – количество импортных костюмов.
Целевая функция, определяющая прибыль универмага имеет вид:
![]()
Ограничения задачи:
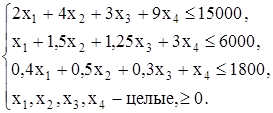
Ограничение по времени: 90´10´2=1800.
Решим задачу, с помощью табличного процессора MSExcel.
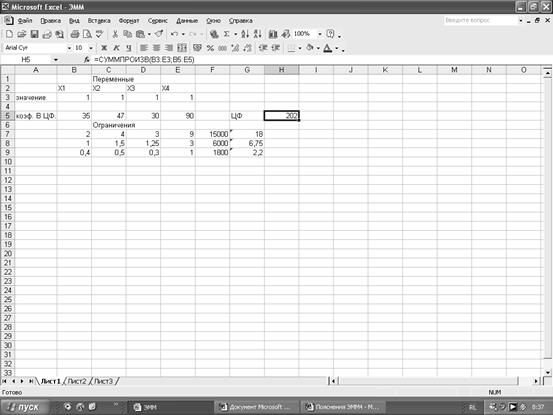
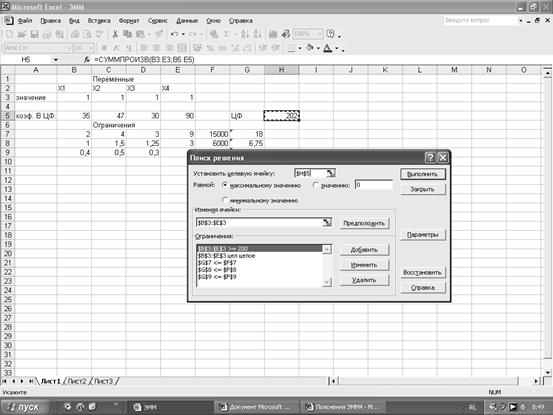
Значения переменных будем получать в ячейках B3:E3. Коэффициенты целевой функции вводим в ячейки B5:E5. Ячейка целевой функции – H5. Поместим в ней курсор, с помощью Мастера функций выберем Категорию Математические и оттуда введем СУММПРОИЗВ, в окне СУММПРОИЗВ указываем адреса массивов B3:E3 и B5:E5.
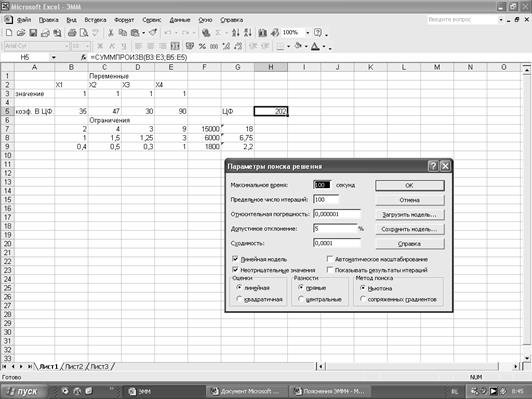
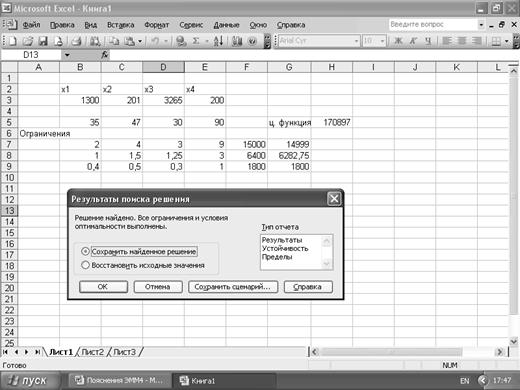
В ячейках B7:E9 вводим коэффициенты ограничений. В ячейках G7:G9 введем правые части системы ограничений, с помощью функции СУММПРОИЗВ. В Поиске решения введем направление целевой функции (максимальное значение), адреса искомых переменных B3:E3, добавим ограничения. Нажимаем кнопку Выполнить. На экране появится сообщение, что решение найдено.
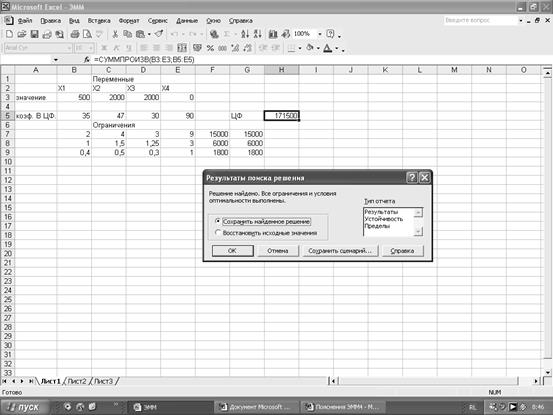
1). Для получения максимальной прибыли в размере 171500 у.е. следует закупить:
500 костюмов из полиэстеровых смесей,
2000 костюмов из шерсти,
2000 костюмов из хлопка и
не закупать дорогие импортные костюмы.
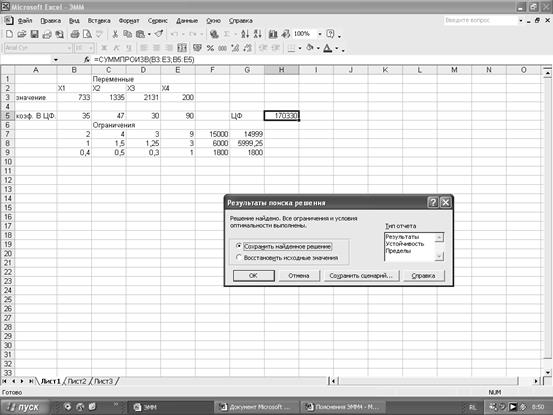
2). При условии, что следует закупить не менее 200 костюмов каждого типа прибыль составит 170330 у.е., что меньше на 1170 у.е. При этом следует закупать:
733 костюма из полиэстеровых смесей,
1335 костюма из шерсти,
2131 костюма из хлопка и
200 импортных костюмов.
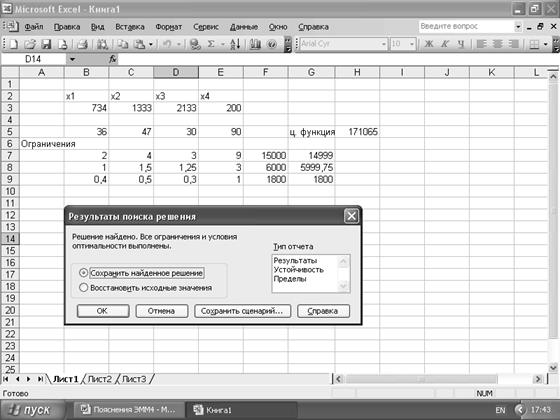
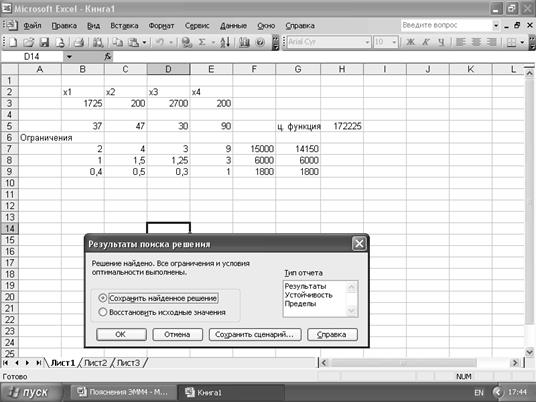
3). Если прибыль от реализации полиэстерового костюма увеличить на 1 у.е. или 2 у.е., то оптимальное решение изменится. В первом случае, максимальная прибыль составит 171065 у.е. при следующих закупках: 734 полиэтеровых костюмов, 1333 шерстяных костюмов, 2133 хлопковых костюмов и 200 импортных костюмов. Во втором случае: максимальная прибыль составит 172225 у.е. при следующих закупках: 1725 костюмов из полиэтеровых тканей, 200 шерстяных, 2700 хлопковых и 200 импортных костюмов.
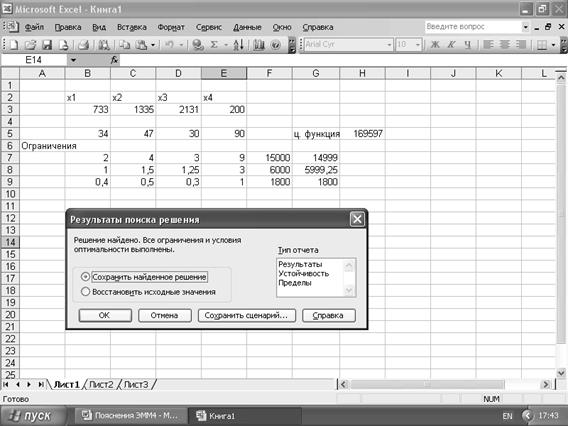
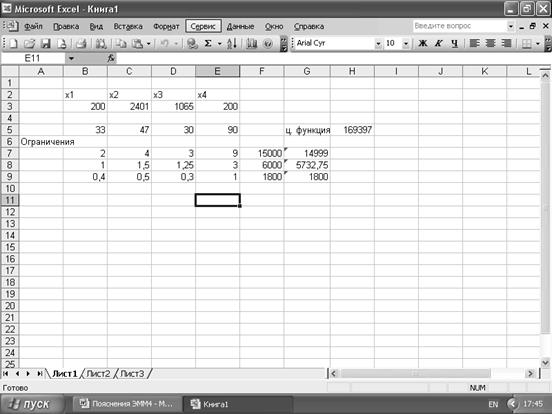
Если прибыль от реализации полиэстерового костюма уменьшить на 1 у.е., то оптимальное решение не изменится, уменьшится лишь получаемая прибыль и составит 169587 у.е. Если прибыль от реализации полиэстерового костюма уменьшить на 2 у.е., то оптимальное решение изменится. В этом случае общая прибыль составит 169397 у.е. при следующих закупках: 200 костюмов из полиэстера, 2401 шерстяных, 1065 хлопковых и 200 импортных костюма.
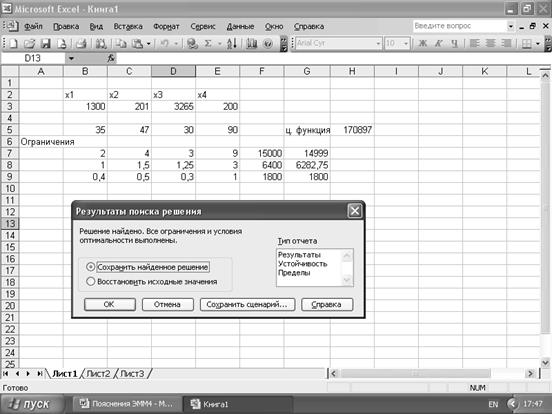
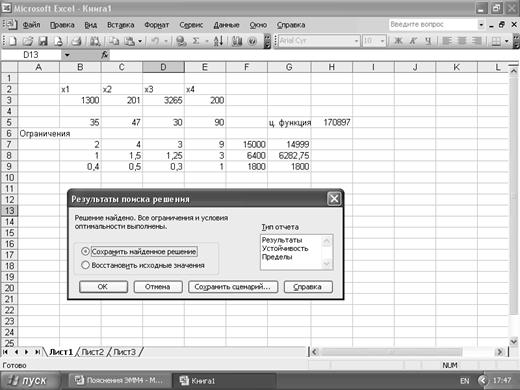
4). Ни увеличение площади, ни увеличение денег на рекламу к увеличению общей прибыли не приводит. При неизменных площадях магазин мог получить прибыль в размере 172250 у.е., при передаче части площади его прибыль составит 170897 у.е. Увеличение денег на рекламу приводит к уменьшению общей прибыли и составит 171056 у.е.
5). Условие о том, что общее число закупленных костюмов не превосходит 5000, выполняется при данных условиях задачи.

Задание 2.4
Распределение аудиторов по фирмам
Менеджер – координатор аудиторской фирмы должен распределить аудиторов для работы на следующий месяц. Есть заявки от 10 клиентов на 75 аудиторов. В четырех конторах фирмы работают 90 аудиторов. 15 аудиторов можно отправить на плановую учебу. Аудиторы различаются по квалификации и опыту работы. Прежде чем приступить к аудиту конкретной фирмы, они должны затратить определенное время на подготовку и консультации. Менеджер – координатор, учитывая опыт работы аудиторов каждой конторы, оценил время, необходимое в среднем аудитору каждой конторы для подготовки к аудиту конкретного клиента. Результаты приведены в таблице. Знаки вопроса в клетках таблицы означают, что аудиторы из этой конторы не имеют опыта аудита в отрасли, которой занимается клиент, и их нельзя посылать к нему. Распределить аудиторов так, чтобы суммарные временные затраты на подготовку были минимальны.
| Конторы | Клиенты | Ресурсы | |||||||||
| К 1 | К 2 | К 3 | К 4 | К 5 | К 6 | К 7 | К 8 | К 9 | К 10 | ||
| А 1 | 8 | 21 | 15 | 13 | 9 | 17 | 18 | 7 | 26 | 9 | 35 |
| А 2 | 14 | 18 | 17 | 19 | 12 | 6 | 0 | 15 | 24 | 13 | 20 |
| А 3 | 9 | 15 | 18 | 16 | 16 | 15 | 11 | 13 | 21 | 19 | 25 |
| А 4 | 11 | ? | 14 | 7 | 23 | 9 | 6 | 18 | ? | 7 | 10 |
| Заявки | 4 | 9 | 2 | 12 | 7 | 6 | 9 | 3 | 18 | 5 | |
В реальной практике обычно требуют, чтобы аудиторы не все были из одной конторы. Попробуйте выполнить это условие и не слишком ухудшить решение.
Решение задачи 2.4
Обозначим через xij
– число аудиторов конторы ![]() , направленные на работу к клиенту
, направленные на работу к клиенту ![]() .
.
Целевая функция, отражающая временные затраты имеет вид:
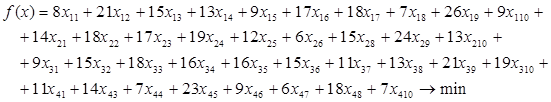
Ограничения, связанные с количеством аудиторов в фирмах и количеством заявок от клиентов, имеют вид:

Поскольку число заявок и число аудиторов в фирмах не совпадают, то введем искусственного клиента, число заявок которого равно 15 и временные затраты на работу равны 0. Система ограничений примет следующий вид:

Решение задачи найдем с помощью табличного процессора MSExcel.
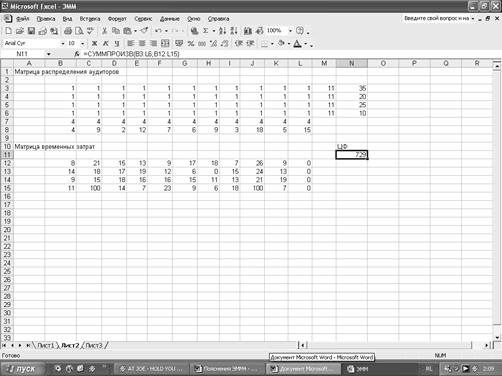
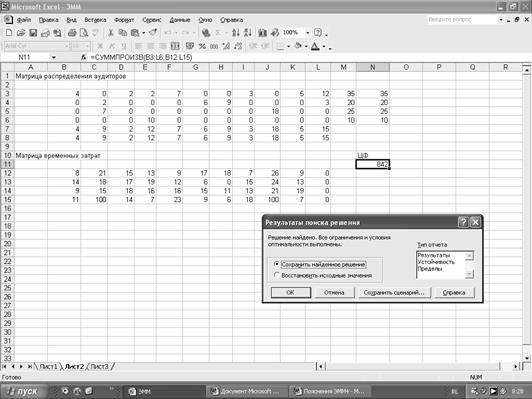
Сформируем матрицу закрепления аудиторов за клиентами. Для этого в блок ячеек B3:L6 вводим «1». В ячейках M3:M6 суммируем по строкам. Число, имеющихся в наличии аудиторов, введем в ячейки N3:N6. В ячейках B7:L7 суммируем по столбцам. Число заявок, поданных клиентами, введем в ячейки B8:L8.
Создаем матрицу временных затрат. Для этого в блок ячеек B12:L15 вводим коэффициенты целевой функции.
Ячейкой целевой функции выберем N11. Поместим в ней курсор, с помощью Мастера функций выберем Категорию Математические и оттуда введем СУММПРОИЗВ, в окне СУММПРОИЗВ указываем адреса массивов B3:L6 и B12:L15.
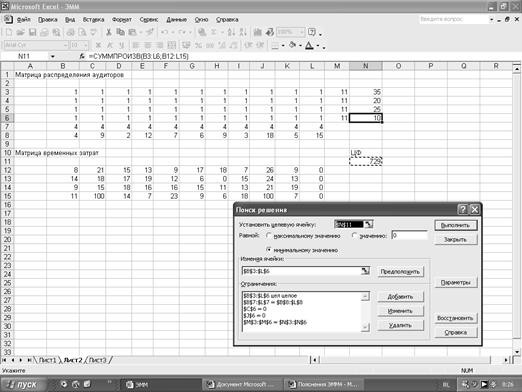
Решение задачи найдем с помощью надстройки Поиск решения.
Поместим курсор в поле Установить целевую (ячейку), введем адрес $N$11, установим направление изменения целевой функции, равное Минимальному значению, введем адреса изменяемых ячеек $B$3:$L$6.
Добавим ограничения:
введем адреса $M$3:$M$6=$N$3:$N$6,
тем самым мы реализуем условие использования всех, имеющихся в наличии аудиторов.
Далее добавляем условие выполнения всех заявок:
выбираем Добавить ограничение,
введем адреса $B$7:$L$7=$B$8:$L$8,
Затем вводим условие целочисленности изменяемых ячеек:
выбираем Добавить ограничение,
введем адреса $B$3:$L$6= целое.
Теперь добавляем условие, что аудиторы фирмы А 4 не могут работать на клиентов К2 и К9.
Используя Параметры, введем условия неотрицательности переменных и линейную модель.
После введения всех ограничений, нажимаем Выполнить, на экране появляется диалоговое окно Результаты поиска решения. Получен оптимальный план распределения аудиторов, он означает следующее:
у клиента К1 работают 4 аудитора фирмы А1,
у клиента К2 – 2 аудитора фирмы А2 и 7 аудиторов фирмы А3,
у клиента К3 – 2 аудитора фирмы А1,
у клиента К4 – 2 аудитора фирмы А1 и 10 аудиторов фирмы А4,
у клиента К5 – 7 аудиторов фирмы А1,
у клиента К6 – 6 аудиторов фирмы А2,
у клиента К7 – 9 аудиторов фирмы А2,
у клиента К8 – 3 аудитора фирмы А1,
у клиента К9 – 18 аудиторов фирмы А3,
у клиента К10 – 5 аудиторов фирмы А1,
12 аудиторов фирмы А1 и 3 аудитора фирмы А2 отправляются на плановую учебу. При этом временные затраты составят 842 ед.
В качестве примера выполнения условия о том, чтобы не все аудиторы были из одной фирмы можно привести следующее распределение аудиторов:
у клиента К1 работают 3 аудитора фирмы А1 и 1 аудитор фирмы А3,
у клиента К2 – 2 аудитора фирмы А2 и 7 аудиторов фирмы А3,
у клиента К3 – 1 аудитор фирмы А1 и 1 аудитор фирмы А4,
у клиента К4 – 6 аудитора фирмы А1 и 6 аудиторов фирмы А4,
у клиента К5 – 6 аудиторов фирмы А1 и 1 аудитор фирмы А2,
у клиента К6 – 5 аудиторов фирмы А2 и 1 аудитор фирмы А4,
у клиента К7 – 8 аудиторов фирмы А2 и 1 аудитор фирмы А4,
у клиента К8 – 2 аудитора фирмы А1 и 1 аудитор фирмы А3,
у клиента К9 – 16 аудиторов фирмы А3 и 2 аудитора фирмы А2,
у клиента К10 – 4 аудитора фирмы А1 и 1 аудитор фирмы А4,
13 аудиторов фирмы А1 и 2 аудитора фирмы А2 отправляются на плановую учебу. При этом временные затраты составят 888 ед.
8-09-2015, 14:27
