Введение
Производство горных работ сопровождается нарушением начального напряженного состояния породных массивов. Горные работы всегда связаны с образованием выработанных пространств в породном массиве или горных выработок. Окружающие выработку горные породы перемещаются в сторону выработанного пространства, причем величина этих перемещений тем больше, чем ближе горные породы расположены к породному обнажению, т. е. вмещающий горную выработку породный массив деформируется. Деформации растяжения в направлении выработки (в «радиальном» направлении) сопровождаются деформациями сжатия во взаимно перпендикулярных направлениях (в «окружном» и «продольном» направлениях), которые обычно совпадают с направлениями очертания контура выработки. Возникающие вокруг выработки деформации растяжения и сжатия горных пород определяют появление соответствующих по знаку и величине дополнительных напряжений, которые искажают или нарушают начальное напряженное состояние породных массивов.
Вокруг горных выработок формируется новое напряженно-деформированное состояние, которое наиболее существенно отличается от начального вблизи контура выработок и практически не отличается вдали от контура. Другой характерной чертой нового напряженно-деформированного состояния вокруг выработок обычно является относительное увеличение или концентрация «окружных» нормальных напряжений и относительное уменьшение или деконцентрация «радиальных» нормальных напряжений. Концентрация напряжений формирует так называемые области опорного давления, а деконцентрация — области разгрузки в породном массиве.
Если новое напряженно-деформированное состояние превосходит некоторый предельный для породного массива уровень, начинается его разрушение, которое в свою очередь изменяет напряженно-деформированное состояние вокруг выработок. Концентрация напряжений или опорное давление смещается вглубь массива, разгружая его приконтурную область. Разрушение на контуре выработок может носить спокойный статический характер или динамический в виде горных ударов и выбросов. Но даже при статическом разрушении горных пород они представляют опасность для нормальной эксплуатации выработок, так как могут потерять устойчивость и обрушиться в выработку.
Таковы самые общие качественные закономерности геомеханических процессов, независимо от того, где они имеют место: вокруг капитальных, подготовительных или очистных выработок, при разработке пластовых или рудных месторождений, при подземных или открытых горных работах.
Для анализа геомеханических процессов используется физическое и математическое моделирование. Среди физических методов моделирования чаще всего применяется моделирование на эквивалентных материалах и на оптически активных материалах.
Напряженно–деформированное состояние массива
В массиве горных пород проводится горно-разведочная выработка круглого сечения. Считая, что в выработке поддерживается температура воздушной среды равной естественной температуре мерзлой породы. Этим самым обеспечиваем только механическое влияние выработки на напряженно – деформированное состояние массива. Как показал анализ эксплуатации горных выработок в многолетних мерзлых породах, существенное влияние на устойчивость породных обнажений оказывает тепловой режим выработки. Поэтому изменение НДС массива будет зависеть только от мерзлого или талого состояния горных пород. Следовательно, можно разделить понятия теплового и механического влияния выработки для правильного понимания деформационных процессов, протекающих в мерзлом и оттаивающем мерзлом массиве пород.
Рассмотрим многолетнемерзлый массив горных пород. Считаем, что в данном массиве стабилизировалось напряженно-деформированное состояние массива (НДС) под влиянием длительного геологического периода (сотни тысяч лет) в процессе формирования “вечной” мерзлоты. К моменту проведения горной выработки в таком массиве пород НДС следует считать исходным или естественным полем напряжений и деформаций. Надо отметить, что “стабилизация НДС” действует в пределах небольшого геологического периода (тысячи и сотни лет). Колебания для значительных геологических формаций, достигающие больших амплитуд, могут влиять на геомеханическое состояние верхнего слоя земной коры, которые, однако, не значимы при анализе НДС массива на срок существования горной выработки (десятки лет).
В районах распространения сплошной мерзлоты, наиболее характерной для месторождений Северо-востока, обычно выделяют три зоны по мощности мерзлого слоя массива горных пород, отличающиеся температурным режимом. Первая зона относится к слою массива пород, прилегающих к дневной поверхности, и называется зоной сезонных годовых колебаний температуры пород (иногда ее называют-гелиотермозоной). В этой зоне колебания температуры пород обусловлены внешними факторами (тепловым режимом атмосферы, солнечной радиацией и т.д.). Мощность данной зоны составляет 10-20 м (в зависимости от географического района расположения месторождения).
Вторая зона – наиболее большая по мощности и представляющая значительный интерес при анализе НДС массива пород вокруг выработок – называется зоной естественного распределения температурного поля. В этой зоне практически не сказывается тепловое влияние внешней среды и глубинного тепла Земли.
Третья зона является переходной между зоной естественного распределения температурного поля и талым массивом горных пород ниже многолетней мерзлоты. Температура пород в этой зоне независимо от различных факторов имеет значения близкие к нулевой изотерме, хотя мощность зоны существенным образом зависит от величины теплового потока, идущей от ядра Земли. Принимаемая за основу разделение многолетнемерзлых горных пород на зоны по мощности, считаем ее соответствие влиянию распределения НДС массива в естественном состоянии.
При проведении вертикальной выработки, которая обычно пересекает всю толщу многолетнемерзлых горных пород, изменение НДС приконтурного слоя породного обнажения будет происходить неодинаково по зонам мерзлоты вследствие различного влияния температурного фактора на геомеханические процессы в массиве вокруг выработки.
В первой зоне, которая в основном сложена дисперсными грунтами и четвертичными отложениями, формирование НДС в мерзлой части промерзающих дисперсных пород связано с развитием таких сложных физико-химических процессов, как кристаллизация поровой влаги и рассучивания породы, миграция незамерзшей воды, расклинивающие действие тонких пленок воды и др. В данной зоне роль температурного фактора весьма значительна в формировании НДС массива пород.
Учитывая вышесказанное, рассмотрим НДС массива многолетнемерзлых горных пород в зоне естественного распределения температурного поля вокруг вертикальной выработки. Будем считать, что действуют две силы, влияющие на НДС массива: гравитационная сила, обусловленная силой тяжести вышележащих горных пород, и температурные напряжения, обусловленные изменением естественного температурного поля горных пород. Если рассматривать НДС массива только от гравитационной силы, то концентрация напряжений на контуре породного обнажения появляется с образованием полости (выработки) в породах. Температурный фактор (например, тепловое воздействие вентиляционного воздуха на естественный температурный режим приконтурного слоя мерзлых пород) вызывает появление температурных напряжений в массиве от температурной зависимости физико-механических свойств и температурного расширения горных пород, что увеличивает или снижает общую концентрацию напряжений на контуре в зависимости от времени проведения выработки и носит сезонный цикличный характер. При проведении вертикального ствола в холодный период времени, когда температура воздуха в выработке бывает значительно ниже естественной температуры пород, приконтурный слой переохлаждается. Это вызывает увеличение концентрации напряжений. Если выработка проводится в летний период, когда в ствол поступает вентиляционный воздух с положительной температурой, то вокруг выработки имеем процесс протаивания мерзлых пород, что приводит к качественно новому перераспределению НДС на контуре обнажения, обусловленному изменением геомеханической ситуации вследствие температурной зависимости физико-механических свойств мерзлых пород, особенно при переходе их в талое состояние.
Эти процессы в зависимости от сезона периодически меняются, особенно при длительной эксплуатации выработки.
В массиве мерзлых горных пород проводится вертикальная выработка круглого сечения. Считаем, что в выработке поддерживается температура воздушной среды равная естественной температуре мерзлых пород. Данное условие позволяет исключить тепловое влияние выработки на механическое состояние приконтурного слоя массива пород. Этим самым обеспечиваем только механическое влияние выработки на напряженно-деформированное состояние массива.
Как показал анализ эксплуатации вертикальных выработок а многолетнемерзлых породах, существенное влияние на устойчивость породных обнажений оказывает тепловой режим выработки. Поэтому изменение НДС массива будет зависеть только от мерзлого или талого состояния горных пород. Следовательно, необходимо разделить понятия теплового и механического влияния выработки для правильного понимания деформационных процессов, протекающих в мерзлом и оттаивающем мерзлом массиве пород.
Осесимметричная плоская деформация
Данная постановка задачи характеризуется равенством нулю касательного напряжения τr и вертикальной деформации εz .
Задачу целесообразнее решать методом перемещений, т.к. независимо от применяемого метода решения распределение напряжений и перемещений описываются одними и теми же выражениями.
В задаче плоской деформации, как и в осесимметричных задачах, напряжения и перемещения определяются выражениями, вывод которых не зависит от применяемого метода решения.
Таким образом, плосконапряженное состояние отличается от плоской деформации только значениями перемещений породного массива, а распределение напряжений описываются одинаковыми формулами.
Существуют три метода решения: метод сил, перемещений и смешанный способ. При решении задачи методом сил за основные неизвестные принимаются напряжения, которые определяются в результате интегрирования уравнений равновесия и уравнений неразрывности деформаций, где деформации выражены через напряжения с помощью физических уравнений. В методе перемещений за основные неизвестные принимаются перемещения, определяемые из решения уравнений равновесия, где напряжения предварительно выражаются через перемещения с помощью физических и геометрических уравнений.
При решении задачи смешанным методом за основные неизвестные принимаются некоторые из напряжений и некоторые из перемещений.
Выбор метода решения часто определяется видом граничных условий: при силовых граничных условиях обычно используется метод сил, при кинематических — метод перемещений. В задачах геомеханики, где анализируются геомеханические процессы от действия горного давления, чаще всего используется метод сил.
Плоское напряженное состояние возникает, когда все действующие напряжения параллельны какой-либо одной плоскости.
Плоское напряженное состояние характерно для объектов, у которых один из размеров существенно меньше двух других, например для тонких пластин, нагруженных по контуру силами, параллельными их плоскости. В частности, если в гравитационном поле сил в массиве пород вокруг вертикального ствола мысленно выделить тонкий слой, перпендикулярный к его оси, то напряженное состояние пород в выделенном слое можно практически полагать плоским.
При наличии плоскости симметрии в породном массиве рассматривается плоская задача. Такой тип задачи обычно используется для исследований механических процессов в окрестности горизонтальных горных выработок.
Решая задачу в постановке плоской деформации, необходимо помнить, что решение будет справедливым только для сечений, которые в процессе деформирования остаются плоскими. В горных выработках такие сечения, нормальные к продольной оси выработки, должны быть удалены от забоя на расстоянии 1 > 6D, где D - пролет поперечного сечения выработки, а в выработках кругового сечения - диаметр. При этом погрешность, возникающая в результате решения задачи в постановке плоской деформации, составляет не более 10%.
Можно предположить, что таков же порядок погрешности при исследовании сечений, расположенных вблизи устьев или сопряжений горных выработок. Отсюда можно сделать и другой вывод: решение задачи в постановке плоской деформации будет весьма грубым приближением для непротяженных выработок и камер с размером по продольной оси 1 < 12D. Остальные выработки, геометрические размеры которых не удовлетворяют этому условию, будут называться протяженными.
Плоская деформация возникает в случае, если перемещения точек деформируемого объема происходят только в одной плоскости. В состоянии плоской деформации находятся средние точки тела, размеры которого в одном каком-либо направлении очень велики, при условии, что не изменяющиеся по значению нагрузки действуют перпендикулярно к этой длинной оси. Например, в гравитационном поле сил в условиях плоской деформации фактически находятся породы вокруг сечения горизонтальной горной выработки.
Модуль упругости
Основной характеристикой деформируемости или деформационных свойств горных пород на допредельной стадии их деформирования является коэффициент связи напряжений и деформаций. На участке линейного упругого деформирования в интервале напряжений от δ1а до δ1с этот коэффициент имеет смысл модуля упругости горной породы при сжатии Ес который численно равен отношению приращения напряжений (δ1с - δ1а ) к приращению продольных деформаций (ε1с . -ε1а ) или тангенсу угла наклона arctg Ес касательной на этом участке диаграммы к оси продольных деформаций. Его величину можно также определить, исключая необратимые деформации путем многократного нагружения с последующей разгрузкой. Поскольку деформирование породных образцов на участке от δ1а до δ1с происходит при закрытых поперечных трещинах и упругом сжатии минерального скелета, наблюдаемый модуль упругости Ес является в основном характеристикой горной породы как материала.
Закон Гука
Для каждого вида приложенных напряжений существует свой коэффициент пропорциональности между напряжениями и упругими деформациями; он является параметром породы, оценивающим ее упругие свойства. Коэффициент пропорциональности между нормальным напряжением (сжимающим или растягивающим) σ и соответствующей ему относительной продольной деформацией υ называется модулем упругости (модулем Юнга) Е:
σ=υ·Ε.
Коэффициент пропорциональности между касательным напряжением τ и соответствующей деформацией сдвига δ’ носит название модуля сдвига G:
τ= G· δ’.
Модуль упругости Е и модуль сдвига G считаются основными упругими характеристиками породы.
Пользуются и другими упругими параметрами пород. В случае объемного напряженного состояния породы связь между напряжением σ и относительным изменением объема ∆V/V выражается через модуль всестороннего сжатия К. Для рыхлых пород пользуются понятием модуля одностороннего сжатия М-коэффициентом пропорциональности между продольным напряжением и соответствующей ему деформацией при расположении пробы в цилиндре с жесткими стенками.
Широко применяют также еще один упругий параметр-коэффициент Пуассона ν, являющийся коэффициентом пропорциональности только между деформациями - относительными продольными ∆l/l и относительными поперечными ∆ d/d:
∆ d/d= ν·∆l/l
Коэффициент Пуассона - величина безразмерная. Он связан с величинами Е и G уравнением:
![]()
Для изотропных тел достаточно знать лишь два упругих параметра; другие параметры могут быть вычислены по соотношениям теории упругости.
Например,
![]()
![]()
Чаще всего в качестве основных параметров экспериментально определяют и используют в расчетах модуль упругости и коэффициент Пуассона.
Расчетная часть
q- напряжения нетронутого массива пород на бесконечности,
E,υ- модуль упругости и коэффициент Пуассона.
2. Распределение полных напряжений в массиве пород вокруг выработки описывается следующим образом
1) σr=q*(1-(1/r²))
σr1=5,8*(1-(1/1,02 ))= 0 Мпа
σr2=5,8*(1-(1/1,12 ))= 1.006 Мпа
σr3=5,8*(1-(1/1,22 ))= 1.772 Мпа
σr4=5,8*(1-(1/1,32 ))= 2.368 Мпа
σr5=5,8*(1-(1/1,402 ))= 2.841 Мпа
σr6=5,8*(1-(1/1,52 ))= 3.222 Мпа
σr7=5,8*(1-(1/1,62 ))= 3.534 Мпа
σr8=5,8*(1-(1/1,702 ))= 3.793 Мпа
σr9=5,8*(1-(1/1,82 ))= 4.009 Мпа
σr10=5,8*(1-(1/1,92 ))= 4.193 Мпа
σr11=5,8*(1-(1/2,02 ))= 4.35 Мпа ,
где σr-радиальное напряжение, r-радиальная координата.
2) σθ= q*(1+(1/r²))
σθ1=5,8*(1+(1/1,02 ))= 11.6 Мпа
σθ2=5,8*(1+(1/1,12 ))= 10.593 Мпа
σθ3=5,8*(1+(1/1,22 ))= 9.827 Мпа
σθ4=5,8*(1+(1/1,32 ))= 9.231 Мпа
σθ5=5,8*(1+(1/1,42 ))= 8.759 Мпа
σθ6=5,8*(1+(1/1,52 ))= 8.377 Мпа
σθ7=5,8*(1+(1/1,62 ))= 8.065 Мпа
σθ8=5,8*(1+(1/1,72 ))= 7.806 Мпа
σθ9=5,8*(1+(1/1,82 ))= 7.590 Мпа
σθ10=5,8*(1+(1/1,92 ))= 7.406 Мпа
σθ11=5,8*(1+(1/2.02 ))= 7.25 Мпа ,
где σθ-тангенциальное напряжение , r-радиальная координата
3. Находим полные радиальные перемещения
Un= q/E*((1- υ)*r+(1+ υ)/r)
U0= q/E*(1- υ)*r,
U= q*(1+ υ)/E*r
- U0-начальное радиальное перемещение
- Un-полные радиальные перемещения
- U-дополнительные радиальные перемещения
1) U0= q/E*(1- υ)*r
U01= (5.8/3.2*104 )*(1-0.2)*1.0= 0.00014
U02= (5.8/3.2*104 )*(1-0.2)*1.1= 0.00015
U03= (5.8/3.2*104 )*(1-0.2)*1.2= 0.00017
U04= (5.8/3.2*104 )*(1-0.2)*1.3= 0.00018
U05= (5.8/3.2*104 )*(1-0.2)*1.4= 0.00020
U06= (5.8/3.2*104 )*(1-0.2)*1.5= 0.00021
U07= (5.8/3.2*104 )*(1-0.2)*1.6= 0.00023
U08= (5.8/3.2*104 )*(1-0.2)*1.7= 0.00024
U09= (5.8/3.2*104 )*(1-0.2)*1.8= 0.00026
U10= (5.8/3.2*104 )*(1-0.2)*1.9= 0.00027
U11= (5.8/3.2*104 )*(1-0.2)*2.0= 0.00029
2) Un= q/E*((1- υ)*r+(1+ υ)/r)
Un1= (5.8/3.2*104 )*((1-0.2)*1.0+1.2/1.0) = 0.000342
Un2= (5.8/3.2*104 )*((1-0.2)*1.1+1.2/1.1) = 0.000337
Un3=(5.8/3.2*104 )*((1-0.2)*1.2+1.2/1.2) = 0.000336
Un4=(5.8/3.2*104 )*((1-0.2)*1.3+1.2/1.3) = 0.000336
Un5=(5.8/3.2*104 )*((1-0.2)*1.4+1.2/1.4) = 0.000338
Un6=(5.8/3.2*104 )*((1-0.2)*1.5+1.2/1.5) = 0.000342
Un7=(5.8/3.2*104 )*((1-0.2)*1.6+1.2/1.6) = 0.000348
Un8=(5.8/3.2*104 )*((1-0.2)*1.7+1.2/1.7) = 0.000354
Un9=(5.8/3.2*104 )*((1-0.2)*1.8+1.2/1.8) = 0.000361
Un10=(5.8/3.2*104 )*((1-0.2)*1.9+1.2/1.9) = 0.000368
Un11=(5.8/3.2*104 )*((1-0.2)*2.0+1.2/2.0) = 0.000377
3) U= q*(1+ υ)/E*r
U1 = 5.8*1.2/ 3.2*104 *1.0 = 0.000217
U2 = 5.8*1.2/ 3.2*104 *1.1 = 0.000239
U3 = 5.8*1.2/ 3.2*104 *1.2 = 0.000261
U4 = 5.8*1.2/ 3.2*104 *1.3 = 0.000282
U5 = 5.8*1.2/ 3.2*104 *1.4 = 0.000304
U6 = 5.8*1.2/ 3.2*104 *1.5 = 0.000326
U7 = 5.8*1.2/ 3.2*104 *1.6 = 0.000348
U8 = 5.8*1.2/ 3.2*104 *1.7 = 0.000369
U9 = 5.8*1.2/ 3.2*104 *1.8 = 0.000391
U10 = 5.8*1.2/ 3.2*104 *1.9 = 0.000413
U11 = 5.8*1.2/ 3.2*104 *2.0 = 0.000435
6. Определяем радиальные и тангенциальные деформации εθ, εr
εθ =(1/E)*(σθ-0.2*σr)
εr=(1/E)*(σr -0.2*σθ)
1) εθ =(1/E)*(σθ-0.2*σr)
εθ1 = (1/3.2*104 )*(11.6-0,2*0.000)= 0.000362
εθ2 = (1/3.2*104 )*(10.593-0,2*1.006)= 0.000324
εθ3 = (1/3.2*104 )*(9.827-0,2*1.772)= 0.000296
εθ4 = (1/3.2*104 )*(9.231-0,2*2.368)= 0.000273
εθ5 = (1/3.2*104 )*(8.759-0,2*2.840)= 0.000255
εθ6 = (1/3.2*104 )*(8.377-0,2*3.222)= 0.000241
εθ7 = (1/3.2*104 )*(8.065-0,2*3.534)= 0.000229
εθ8 = (1/3.2*104 )*(7.806-0,2*3.793)= 0.000220
εθ9 = (1/3.2*104 )*(7.590-0,2*4.009)= 0.000212
εθ10 = (1/3.2*104 )*(7.406-0,2*4.193)= 0.000205
εθ11 = (1/3.2*104 )*(7.25-0,2*4.35)= 0.000199
2) εr=(1/E)*(σr -0.2*σθ)
εr1 = (1/3.2*104 )*(0.000-0,2*11.6)= -0.000072
εr2 = (1/3.2*104 )*(1.006-0,2*10.593)= -0.000034
εr3 = (1/3.2*104 )*(1.772-0,2*9.827)= -0.000006
εr4 = (1/3.2*104 )*(2.368-0,2*9.231)= 0.000016
εr5 = (1/3.2*104 )*(2.840-0,2*8.759)= 0.000034
εr6 = (1/3.2*104 )*(3.222-0,2*8.377)= 0.000048
εr7 = (1/3.2*104 )*(3.534-0,2*8.065)= 0.000060
εr8 = (1/3.2*104 )*(3.793-0,2*7.806)= 0.000069
εr9 = (1/3.2*104 )*(4.009-0,2*7.590)= 0.000077
εr10 = (1/3.2*104 )*(4.193-0,2*7.406)= 0.000084
εr11 = (1/3.2*104 )*(4.35-0,2*7.25)= 0.000090
Заключение
1. Овладел методами решения указанной задачи в полном объёме (метод сил и метод перемещений).
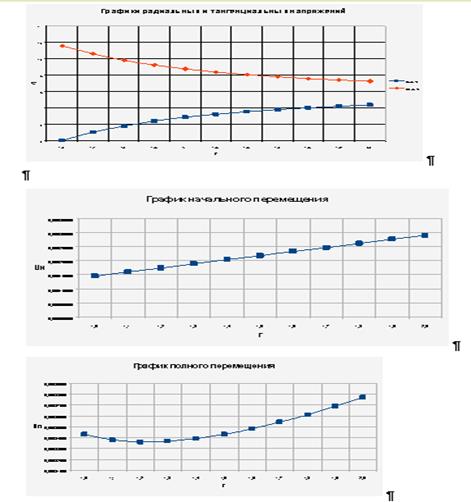
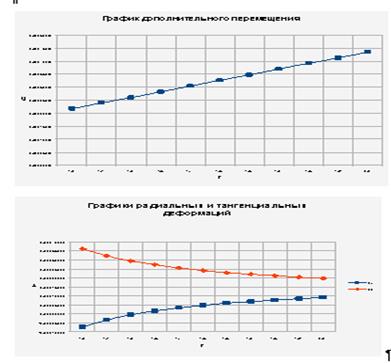
2. Исходя из методов результатов решения, можно заключить, что радиальное напряжение σr имеет прямо пропорциональную зависимость от радиальной координаты r, а тангенциальное напряжение σθ имеет обратно пропорциональную зависимость от r.
Список используемой литературы:
1. Баклашов И.В., Картозия Б.А. Механика подземных сооружений и конструкций крепей. М., 1984. 415 с.
2. Борисов А.А. Механика горных пород и массивов. М., Недра, 1980. 360 с.
3. Булычев Н.С. Механика подземных сооружений. М., Недра, 1982. 272 с.
4. Напряженно-деформированное состояние мерзлого массива пород вокруг вертикального ствола (методические указания)// Составитель Иудин М.М. Якутск, ЯГУ, 1997. 26 с.
29-04-2015, 00:30
