МИНИСТЕРСТВО ОБРАЗОВАНИЯ НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РФ
ГОУВПО «УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСТИТЕТ»
НЕФТЯНОЙ ФАКУЛЬТЕТ
Кафедра «Разработка и эксплуатация нефтяных и газовых месторождений
Специальность 090600 – Разработка и эксплуатация нефтяных и газовых месторождений
КУРСОВАЯ РАБОТА
по дисциплине: «Подземная гидромеханика»
на тему: «Расчет показателей разработки газовой залежи
при упругом режиме разработки».
Вариант №8
Выполнил
студент группы ЗС-090600-32(К) С.М.Зарипова
Проверил:
к.т.н. доцент С.Ю.Борович
Ижевск
2010г.
Содержание
1. Теоретическая часть...........................................................................................3
1.1. Теория упругого режима……..…………………………...............................3
2. Расчетная часть.................................................................................................11
2.1. Подсчитать упругий запас в пласте…….……............................................12
2.2. Рассчитать падение пластового давления во времени при режиме
постоянного отбора газа…………………….................................................14
2.3. Рассчитать динамику отбора газа и пластового давления при режиме
постоянной депрессии на пласт..................................................................17
Вывод....................................................................................................................22
Список литературы..............................................................................................22
- Т
еор
е
тическая часть
.
Теория упругого режима.
Основы теории движения газа в пористой среде были разработаны
основателем советской школы нефтегазовой гидромеханики академиком
Л. С. Лейбензоном, который впервые получил дифференциальные уравнения
неустановившейся фильтрации совершенного газа в пласте по закону
Дарси. Полученное уравнение было названо уравнением Лейбензона.
При выводе указанного уравнения предполагалось, что коэффициенты пористости и проницаемости не изменяются с давлением, т. е. пласт недеформируем, вязкость газа также не зависит от давления, газ совершенный. Принимается также, что фильтрация газа в пласте происходит по изотермическому закону, т. е. температура газа и пласта остается неизменной по времени. Впоследствии один из учеников Л. С. Лейбензона-Б. Б. Лапук в работах, посвященных теоретическим основам разработки месторождений природных газов, показал, что неустановившуюся фильтрацию газа можно приближенно рассматривать как изотермическую, так как изменения температуры газа, возникающие при изменении давления, в значительной мере компенсируются теплообменом со скелетом пористой среды, поверхность контакта газа с которой огромна. Однако при рассмотрении фильтрации газа в призабойной зоне неизотермичность процесса фильтрации сказывается существенно вследствие локализации основного перепада давления вблизи стенки скважины. Кстати, на этом эффекте основано использование глубинных термограмм действующих скважин для уточнения профиля притока газа по толщине пласта (глубинная дебитометрия). При рассмотрении процесса фильтрации в пласте в целом этими локальными эффектами допустимо пренебрегать. Для вывода дифференциального уравнения неустановившейся фильтрации совершенного газа воспользуемся уравнением, которое справедливо для любого сжимаемого флюида:
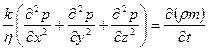 (1)
(1)
где k - коэффициент проницаемости,
m – пористость,
![]() - коэффициент вязкости,
- коэффициент вязкости,
р – давление,
![]() -плотность,
-плотность,
t – время,
m=
const , k=
const , ![]() const .
const .
Функция Лейбензона для совершенного газа определяется по формуле:
P
![]() (2)
(2)
Преобразуем правую часть уравнения (1). Считая пористость m постоянной и учитывая, что для совершенного газа
![]() ,
(3)
,
(3)
получим:
![]() .
(4)
.
(4)
В результате сделанных преобразований получим уравнение относительно только одной неизвестной функции – давления:
![]() .
(5)
.
(5)
Полученное дифференциальное уравнение неустановившейся изотермической фильтрации совершенного газа называется уравнение Л.С. Лейбензона и представляет собой нелинейное дифференциальное уравнение в частных производных параболического типа. Подчеркнем, что оно справедливо при выполнении закона Дарси. Изменение коэффициента пористости пренебрегают потому, что он входит в уравнение в виде произведения ![]() m
, в котором плотность газа изменяется в гораздо большей степени, чем пористость.
m
, в котором плотность газа изменяется в гораздо большей степени, чем пористость.
Уравнение (5) записано в безиндексной форме, справедливой для любой системы координат. В декартовой системе координат уравнение имеет вид
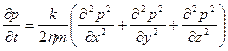 .
(6)
.
(6)
Уравнение (5) можно записать и по-другому, умножив его на давление р и, учитывая, что
![]() ,
(7)
,
(7)
будем иметь
![]()
![]() (8)
(8)
или в декартовой системе координат
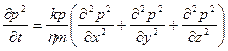 .
(9)
.
(9)
В такой записи под знаком производных по координатах и по времени находится одна и та же функции р2 , но коэффициент перед оператором Лапласа переменный, в него входит искомая функция р( x , y , z , t ).
Нетрудно показать, что неустановившаяся фильтрация реального газа с уравнением состояния
![]() (10)
(10)
и с учетом зависимости коэффициента вязкости от давления ![]() и недеформируемости пористой среды (m
=const , k
=const) описывается следующим нелинейным дифференциальным уравнением параболического типа:
и недеформируемости пористой среды (m
=const , k
=const) описывается следующим нелинейным дифференциальным уравнением параболического типа:
 (11)
(11)
Отметим, что одним из эффективных путей решения уравнения Лейбензона является линеаризация, т.е. сведение его к линейному уравнению Фурье.
Вывод дифференциального уравнения неустановившейся фильтрации совершенного газа по двучленному закону.
Будем считать пласт недеформируемым, фильтрацию изотермической и происходящей по двучленному закону. Рассмотрим плоскорадиальный поток к осесимметрично расположенной скважине.
Воспользуемся уравнением неразрывности для плоскорадиального
движения: ![]() (12)
(12)
Воспользовавшись выражением для массовой скорости р w , получен-
ным из двучленного закона фильтрации (![]() 5.22), и формулами
5.22), и формулами 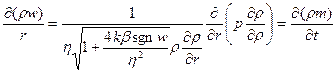 и
и 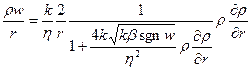 ,
,
после подстановки в них значений плотности из уравнения состояния ![]() получим:
получим:
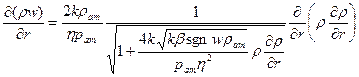 (13)
(13)
 (14)
(14)
Подставив выражения (13), (14) и (4) в уравнение неразрывности
(12) и сократив на р ат
/рат
,
получим: 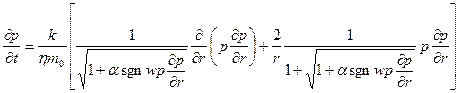 , (15)
, (15)
где ![]()
Если сделать замену ![]() , то дифференциальное уравнение
, то дифференциальное уравнение
неустановившейся фильтрации газа по двучленному закону примет
следующий вид: 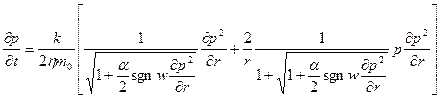
Если заменить нелинейное дифференциальное уравнение (5) или (9) линейным, т.е линеаризовать его, то оно упростится, для линейного уравнения существуют точные аналитические решения. Ясно, что эти точные решения линеаризованного уравнения будут приближенными для нелинейного. Оценить погрешность решения, которая возникает при замене точного уравнения линеаризованным, можно, например, сравнивая приближенное решение с решением на ЭВМ точного уравнения.
Были предложены различные способы линеаризации уравнения (5) или (9). Если рассматривается плоскорадиальный приток к скважине, то, как известно из теории установившейся фильтрации газа, воронка депрессии очень крутая, и в большей части пласта давление мало отличается от контурного. На этом основании Лейбензон предложил заменить переменное давление р
в коэффициент перед оператором Лапласа в уравнении (9) на постоянное давление рк
, равное начальному давлению в пласте. Тогда, обозначив ![]() , получим вместо уравнения (9) уравнение
, получим вместо уравнения (9) уравнение
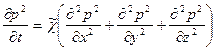 ,
(16)
,
(16)
которое является линейным уравнением пьезопроводности относительно функции р2
(![]() - коэффициент пьезопроводности). Такой способ линеаризации, когда переменный коэффициент
- коэффициент пьезопроводности). Такой способ линеаризации, когда переменный коэффициент ![]() в уравнении (16) при различных значениях давления принимается константой, называется линеаризацией по Лейбензону. В дальнейшем различными авторами были предложены уточнения к линеаризации по Лейбензону. Так, И.А. Чарный предложил свести уравнение (9) к линейному заменой переменного давления в коэффициенте на значение
в уравнении (16) при различных значениях давления принимается константой, называется линеаризацией по Лейбензону. В дальнейшем различными авторами были предложены уточнения к линеаризации по Лейбензону. Так, И.А. Чарный предложил свести уравнение (9) к линейному заменой переменного давления в коэффициенте на значение
![]()
где pmax и pmin – максимальное и минимальное давления в газовой залежи на расчетный период.
Используем линеаризованное уравнение (16) для решения конкретной задачи о притоке газа в скважину бесконечно малого радиуса (точечный сток), расположенную в пласте бесконечной протяженности с постоянной толщиной h . В начальный момент времени пласт невозмущен, т.е. давление во всем пласте постоянно и равно pk . С этого момента начинается отбор газа с постоянным дебитомQ ат . Нужно найти изменение давления по пласту с течением времени p ( r , t ).
Для плоскорадиальной фильтрации газа (16) запишется следующим образом :
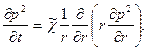 (17)
(17)
Здесь выражение 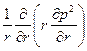 представляет собой оператор Лапласа в полярных координатах относительно квадрата давления для плоскорадиального движения.
представляет собой оператор Лапласа в полярных координатах относительно квадрата давления для плоскорадиального движения.
Уравнение (17) надо проинтегрировать при начальном условии
p 2 = p 2 k при t = 0, 0<r < ∞ (18)
и при граничном условии в удаленных точках
p 2 = p 2 k при r =∞ , t > 0. (19)
Выведем условие для давления на забое скважины. Для этого запишем выражение для массового дебита исходя из закона Дарси в дифференциальной форме для плоскорадиальной фильтрации:
![]()
Использовав равенства ![]()
![]()
и сократив па p ат , получим :
![]()
Из этого соотношения выразим условие на стенке газовой скважины бесконечно малого радиуса:
![]() при r
=0. (20)
при r
=0. (20)
Таким образом, для решения поставленной задачи уравнение (13) должно быть проинтегрировано при условиях (18), (19) и (20).
Решением поставленной задачи для упругой жидкости является основная формула упругого режима:
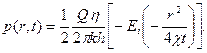 (21)
(21)
Аналогия между фильтрацией упругой жидкости и газа свидетельствует о том, что, заменив в формуле (21) давление на р2
,
![]() на
на ![]() ,
, ![]() на
на ![]() , получим решение поставленной задачи для газа:
, получим решение поставленной задачи для газа:
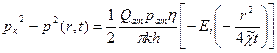 (22)
(22)
или
 (23)
(23)
Это и есть основное решение линеаризованного уравнения Лейбензона.
Для малых значений аргумента ![]() можно заменить интегральную функцию логарифмической
можно заменить интегральную функцию логарифмической
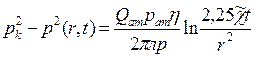 (24)
(24)
или
![]() (25)
(25)
Подчеркнем, что решения (22)-(25) являются приближенными, т.к. получены в результате интегрирования линеаризованного уравнения Лейбензона.
Формула (23) и (25) определяют при фиксированных значениях времени распределение давления вокруг газовой скважины, работающей с постоянным дебитом с момента t=0. Эти депрессионные кривые имеют такой же характер, как и при установившейся фильтрации – они очень крутые вблизи скважины (рис.1а). Если задать значение r , то можно найти изменение давления в данной точке с течением времени. В частности, можно найти изменение давления на забое (при r = rc ) после работы скважины (рис.1б):
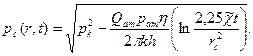 (26)
(26)

Рис.1.Кривые восстановления по пласту при неустановившемся притоке газа к скважине в разные моменты времени (а) и динамика распределения давления в фиксированных точках пласта (б).
2.Расчетная часть.
Основные исходные данные
| № п/п | Показатели | Единица измерения | Символическое обозначение | Величина |
| 1 | Средняя эффективная газонасыщенная толщина | м | h | 10 |
| 2 | Коэффициент открытой пористости | доли ед. | т | 0,2 |
| 3 | Коэффициент проницаемости | мкм2 | k | 0,29 |
| 4 | Коэффициент динамической вязкости газа | Па·с | η | |
| 5 | Радиус контура питания | м | RK | 300 |
| 6 | Радиус скважины | м | r | 0,08 |
| 7 | Плотность газа | кг/м3 | ρ | 0,076 |
| 8 | Давление на контуре | МПа | рк |
9,6 |
| 9 | Давление на забое | МПа | рс | 8,7 |
| 10 | Коэффициент пьезопроводности | м2 /с | 0,0738 |
|
| 11 | Атмосферное давление | Па | Рат | 0,1·106 |
| 12 | Площадь предела контакта газоносности | км2 |
F |
4879,95 |
| 13 | Коэффициент газонасыщенности | % | 75,5 | |
| 14 | Коэффициент газоотдачи | % | 70 | |
| 15 | Стандартная температура | К | Т | 273 |
| 16 | Коэффициент сверхсжимаемости | z | 0,838 |
2.1. Подсчет упругого запаса газа в пласте.
Подсчет упругого запаса газа в пласте рассчитаем по объемному методу
![]() , (форм.XVI.1) [3]
, (форм.XVI.1) [3]
где F- площадь в пределах продуктивного контура газоносности, м2
h – мощность пористой части газоносного пласта, м
m – коэффициент пористости,
f – поправка на температуру для приведения объема газа к стандартным
условиям,
p – среднее давление в залежи на дату расчета, МПа
pк – среднее остаточное (конечное) давление в залежи после извлечения
промышленных запасов газа и установления на устье скважины
абсалютного давления, равного 0,1 МПа, МПа
α,αк – поправка на отклонение углеводородных газов от закона Бойля-
Мариотта соответственно для р и рк
βг - коэффициент газонасыщенности
ηг – коэффициент газоотдачи.
![]() , где
, где
tct =20º C – cтандартная температура
Примем температуру пласта tпл =27º С
![]()
![]() , где примем z=0,838 – коэффициент сверхсжимаемости,
, где примем z=0,838 – коэффициент сверхсжимаемости,
αк =1 при рат
![]()
![]() по форм.3.39 [1]
по форм.3.39 [1]
Примем Н=2000м – глубина скважины
ρГ = 0.7 – плотность газа по воздуху
![]() по форм.V.5[3]
по форм.V.5[3]
![]()
2.2. Расчет падения пластового давления во времени при режиме постоянного отбора газа.
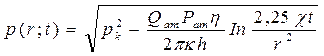 , p = pк
, p = pк
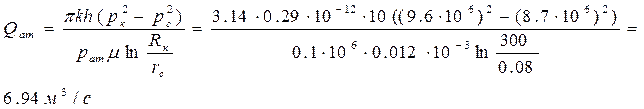
При t=1 ч = 3600 с
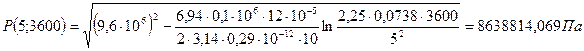
![]()
При t = 1 сут = 86400 с
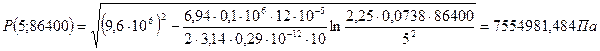
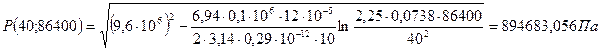
При t = 10 сут = 864000 с
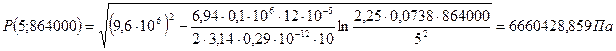
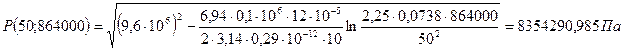
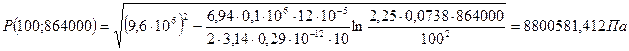
При t = 50 сут = 4320000 с
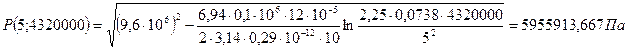
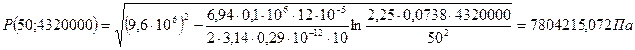
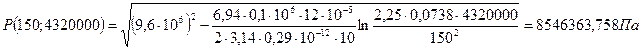
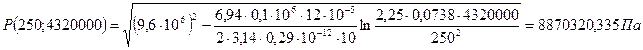
При t = 300 сут = 25920000 с
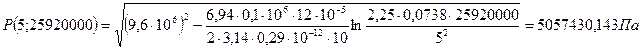
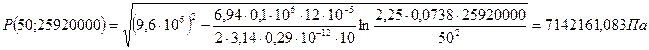
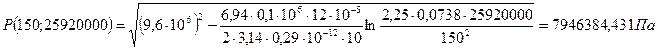
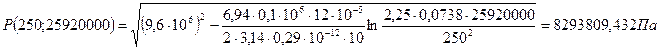
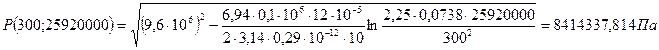
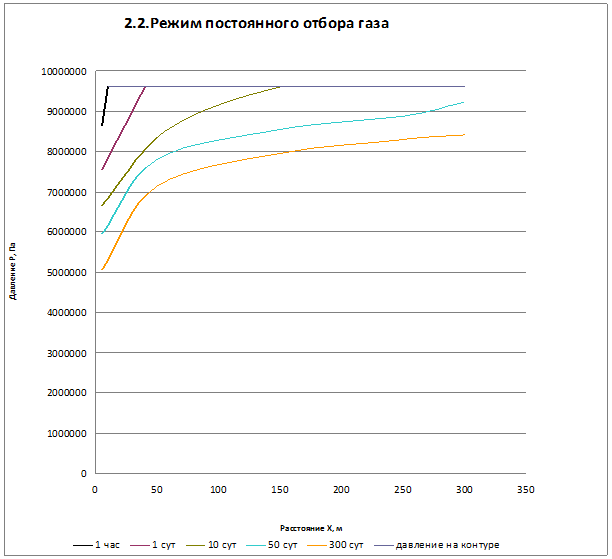
Вывод: Эти кривые имеют такой же характер, как и при установившейся фильтрации – они очень крутые в близи скважины. При изменении значения r, изменяется давление в данной точке с течением времени, т.е. давление будет понижаться.
2.3. Расчет динамики отбора газа и пластового давления при режиме постоянной депрессии на пласт.
1) Расчет динамики отбора газа при режиме постоянной депрессии на пласт.
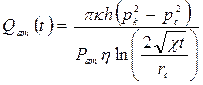
При t = 1 ч = 3600 с
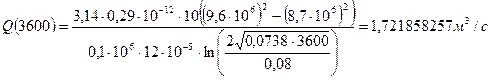
При t = 1 сут = 86400 с
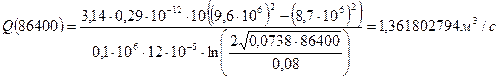
При t = 10 сут = 864000 с
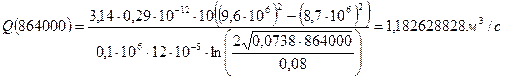
При t = 50 сут = 4320000 с

При t = 300сут = 25920000 с
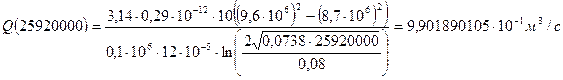
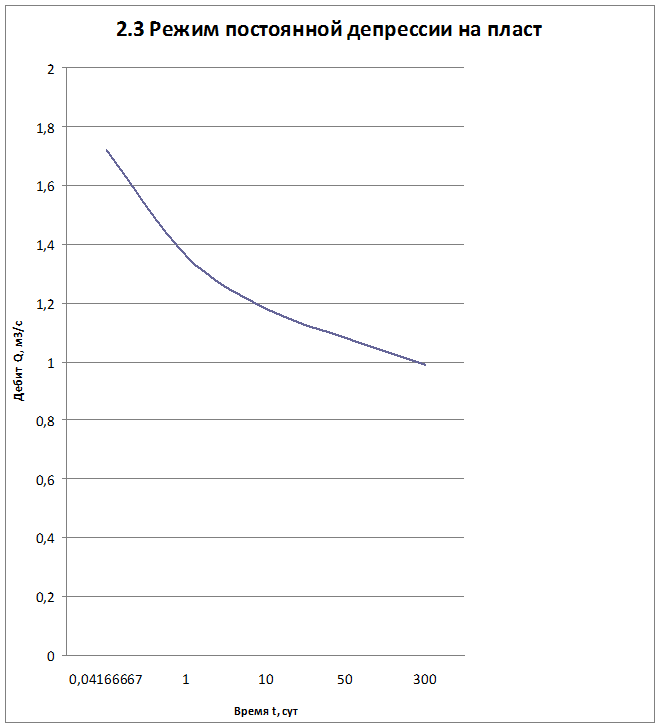
Вывод: Из графика видно, что стечением времени дебит уменьшается, т.е. количество газа, извлеченного из пласта за некоторый промежуток времени, равно изменению запасов газа в пласте, т.к. пласт замкнут,то запасы ограничены и не пополняются из вне.
2) Расчет пластового давления при режиме постоянной депрессии на пласт.
Метод последовательной смены стационарных состояний
![]()
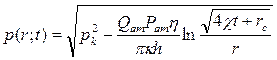
, ![]() ,
, ![]()
При t = 1 ч = 3600 с ![]()
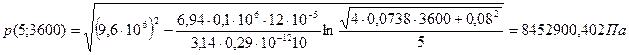
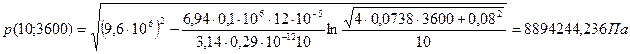
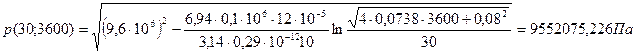
![]()
При t = 1 сут = 86400 с ![]()
![]()
![]()
![]()
![]()
![]()
При t = 10 сут = 864000 с ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
При t = 50 сут = 4320000 с ![]()
![]()
![]()
![]()
![]()
![]()
![]()
При t = 300 сут = 25920000 с ![]()
![]()
![]()
![]()
![]()
![]()
![]()
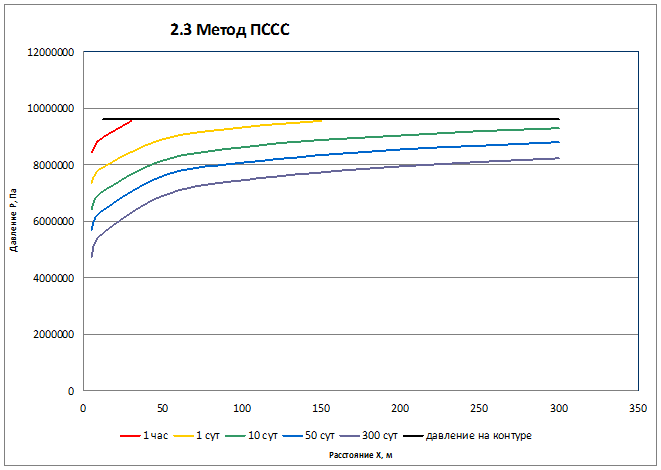
Вывод: Из графика видно, что с изменением значения r, изменяется давление в данной точке пласта с течением времени, т.е. давление будет понижаться.
Литература:
1. Басниев К.С. и др. Подземная гидромеханика. М.: Недра, 1993 г., 181-188 с., 199-201 с.
2. Борхович С.Ю. Подземная гидромеханика. Учебно-методическое пособие (для специальности РЭНГМ). Ижевск, 2005 г.
3. Жданов М.А. Нефтегазопромысловая геология и подсчет запасов нефти
и газа. М.: Недра, 1981.-453с
29-04-2015, 00:32
