Міністерство аграрної політики України.
Державна агроекологічна академія України.
Кафедра моніторингу НПС
Курсова робота
на тему:
“Гідрологічні та водогосподарські розрахунки”
Виконав: студент 2 курсу
1 групи екологічного факультету
Касянчук В.В.
Перевірив: Дорошенко В.В.
Житомир 2001
Завдання курсової роботи
| Назва річки | Кам’янка |
| Річка – аналог | Уборть |
| Площа водозабору | 260 км2 |
| Роки | 1961 – 1975 |
| К-ть голів тварин | 2900 |
| К-ть води, використаною однією головою | 65 л/добу |
| М, м3 /га | 850 |
| Площа дзеркала | 150 |
| Грунт | Глина |
| Зарегульваність стоку | 0,01 |
Зміст
Вступ
1. Гідрографічна характеристика річки
2. Гідрологічні розрахунки
2.1 Визначення норми стоку
2.2 Визначення коефіцієнтів варіації та асиметрії
2.3 Забезпеченість, її визначення і будова кривої забезпеченості при обмежений кількості даних
2.4 Побудова аналітичної кривої забезпеченості
2.5 Побудова кривих повторюваності і забезпеченості рот достатній кількості даних
3. Регулювання стоку
3.1 Визначення місця розташування і притоку води до водосховища
3.2 Складові частини водосховища
3.2.1 Мертвий об'єм
3.2.2 Корисний об'єм
3.2.3 Форсований об'єм
3.3 Проектування греблі
4. Внутрірічний розподіл стоку
5. Визначення скидних витрат з водосховища і розмірів гідроспоруд
Список літературних джерел
Додатки
Вступ
Мета курсової роботи - навчитись давати кількісну оцінку гідрологічним явищам, визначити статистичні характеристики стоку, виконувати водогосподарські розрахунки.
Основою для виконання курсової роботи є фактичні дані річки з певним періодом спостережень за її стоком і гідрографічною характеристикою. Ці відомості отримані з завданням, а також з гідрографічного опису річки.
Курсова робота складається з розрахунково-пояснювальної записки і графічної частини. В пояснювальній записці стисло викладаються необхідні описи і розрахунки, а також розрахункові таблиці. Записка закінчується загальними висновками, списком використаної літератури.
До графічної частини роботи відносяться план, повздовжній переріз водосховища і поперечний — греблі, гістограма розподілу і крива забезпеченості. Усі ці креслення, крім плану водосховища, виконані в масштабі на стандартних аркушах та на міліметрове му папері.
1. Гідрографічна характеристика річки
Річка Камя’нка бере початок на відстані 0,5 км. Захініше с. Ярешки на висоті 235м над рівнем моря і впадає у р. Рось зліва, на 213 км від її гирла біля с. Чмирівка на висоті 152 м над рівнем моря. Довжина річки – 105 км; площа водозбору 840 км2 , середній ухил водної поверхні 0,79%0.
Основна притока: р. Собот (п.б., 18 км).
Басейн річки розміщений в межах Придніпровського підвищення, має грушевидну форму. Довжина його - 83 км, середня ширина - 10 км; у верхній частині ширина його не перевищує 7,5 км, а в нижній - збільшується до 25 км. Поверхня басейну рівнинна. Грунти крупно-пилуваті, легкосуглинкові, чорноземні.
Річкова сітка розвинена добре; коефіцієнт густоти її з врахуванням річок менше 10 км складає 0,37 км, а без урахування їх – 0,18.
Долина слабо звивиста, трапецевидна, і тільки біля сс. Бертники, Фурси – у – подібна. Переважаюча ширина її 0,9 – 1,2 км, найбільша - 3,5 км(с. Дрозди), найменше – 0,3 км(с. Фурси).
Схили висотою – 15 – 25 м переважно випуклі, помірно круті, рідше круті, або пологі, слабо розсічені і тільки між с. Трилеси і с. Мазепинці – правий - сильно розсічений. Складені вони суглинковими ґрунтами, розорені або зарослі степовими травами, біля сс. Парипси, Саверці, Ставище, Кожанка, Червона, і між сс. Дрозди і Безугляки покриті змішаними лісами (дуб, сосна, береза).
Пойма лучна, суха двостороння, місцями чергується по берегам(сс. Зубарі, Кожанка, Корольовка, Дрозди, Велико-Половецьке). Переважаюча ширина її 200 – 400 м, місцями звужується до 100 – 70 м (сс. Дрозди, Безугляки) або розширюється до 1,2 км (верхня околиця с. Парипси).
Поверхня пойми – рівна, перетинається улоговинами і торф’яними кар’єрами; складена вона суглинковими ґрунтами. В верхній течії зустрічається заболочені ділянки, складені торф’яними ґрунтами. В період весняного паводку пойма затоплюється на 1 – 3 неділі шаром води до 2 – 2,5 м.
Русло слабо звивисте, не розгалужене, до с. Трилеси є рядом окремих плесів, місцями воно губиться в заболоченій поймі. Переважаюча ширина річки 5 – 10 м, найбільша – 25 м (с. Трилеси). Глибина близько 0,3 – 0,8 м, найбільша – 3,6 м; швидкість рідко досягає 0,2 м/с.
Річка протікає через ряд ставків – водосховищ довжиною від 0,2 до 4,9 км, шириною від 20 до 450 м. гглибиною від 0,5 – 4,0м, біля берегів (місцями по всій ширині) русло заростає водною рослинністю. Дно рівне замулене або торф’янисте, місцями кам’яне.
Берега висотою 0,5 – 1,5 м, круті, обривисті, зрідка плоскі, порослі очеретом та осокою, місцями – чагарником і окремими деревами. Складені вони торф’янистими ґрунтами, в с. Фурси – кам’яне. Внаслідок зарегульованості річки її природний режим значно порушений. Гирлова ділянка річки знаходиться у змінному підпорі від річки Рось.
2. Гідрологічні розрахунки
Гідрологічні розрахунки мають різну мету. В залежності від кількості спостережень (довжини ряду) методи розв’язання завдань не зовсім однакові. Спочатку визначаємося основні характеристики стоку6 середньоаріфметична величина або норма стоку, коефіцієнти варіації і асиметрії.
Слід пам’ятати, що стік може бути представлений у вигляді різних параметрів і одиниць.
Це витрати Q, модуль q, шар h, об’єм V3 відповідними одиницями м3 /c, л /с км2 , мм і м3 . Всі вони переводяться з одних в інші за допомогою простіших залежностей.
2.1 Визначення норми стоку
При достатній кількості даних (біля 300 років) норма стоку визначається як середня арифметична даного ряду, тобто
∑ Qi
Q = --------- (2)
n
де n – число членів ряду.
При нестачі даних (n < 30 років) виникає потреба в продовженні ряду по більш довгому ряду річки – аналогу. Для цього може бути використаний метод парної регресії.
Відібравши річку-аналог, або створ даної річки, з довгим періодом спостережень (в нашому випадку річка-аналог вказана в завданні), і використовуючи короткий ряд по основній річці, яка також вказана в завданні (додаток 2), одержують рівняння регресії, що має такий вигляд:
Qi - Qcp = r (QAI – QAcp ) (3)
Де Qi і Qai – витрати даної річки і річки-аналогу в будь-який рік спостережень;
Qcp i QAcp – cередні значення витрат за загальний період спостережень;
уQ i уQA – середньоквадратичні відхилення рядів даної річки і аналогу від середнього значення;
r – коефіцієнт кореляції.
| №№ п/п | Рік | Q, м3 /с |
QA , м3 /с | ДQ | ДQА | ДQ2 | ДQА 2 | ДQДQА |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1961 | 5,4 | 13,0 | -4,9 | -0,7 | 24,01 | 0,49 | 3,93 |
| 2 | 1962 | 18,6 | 20,9 | 8,3 | 7,2 | 68,89 | 51,84 | 59,76 |
| 3 | 1963 | 4,7 | 6,0 | -5,6 | -7,7 | 31,36 | 59,29 | 43,12 |
| 4 | 1964 | 5,1 | 6,2 | -5,2 | -7,5 | 27,04 | 56,25 | 39,00 |
| 5 | 1965 | 6,0 | 7,8 | -4,3 | -5,9 | 18,49 | 34,81 | 25,37 |
| 6 | 1966 | 12,3 | 17,8 | 2,0 | 4,1 | 4,00 | 16,81 | 8,2 |
| 7 | 1967 | 10,4 | 13,4 | 0,1 | -0,3 | 0,01 | 0,09 | -0,03 |
| 8 | 1968 | 13,6 | 17,6 | 3,3 | 3,9 | 10,89 | 15,21 | 12,87 |
| 9 | 1969 | 14,9 | 21,5 | 4,6 | 7,8 | 21,16 | 60,84 | 35,88 |
| 10 | 1970 | 19,6 | 28,4 | 9,3 | 14,7 | 86,49 | 216,09 | 136,81 |
| 11 | 1971 | 17,5 | 21,0 | 7,2 | 7,3 | 51,84 | 53,29 | 52,56 |
| 12 | 1972 | 6,1 | 8,3 | -4,2 | -5,4 | 17,64 | 2916 | 22,68 |
| 13 | 1973 | 5,9 | 7,4 | -4,4 | -6,3 | 19,36 | 39,69 | 27,72 |
| 14 | 1974 | 4,0 | 7,0 | -6,3 | -6,7 | 39,69 | 44,89 | 42,21 |
| 15 | 1975 | 6,4 | 9,3 | -3,9 | -4,4 | 15,21 | 19,36 | 17,16 |
| S | 154,5 | 205,5 | 436,08 | 698,11 | 526,64 |
Розрахунки починають з визначення коефіцієнта кореляції за формулою:
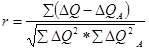 (4)
(4)
де ДQ і ДQА – різниця між будь-якими і середніми значеннями даної річки і аналогу.
![]() =0,95
=0,95
Середні квадратичні відхилення, в свою чергу, визначаємо за формулами
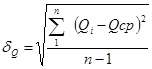 (5)
(5)
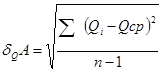 (6)
(6)
![]() = 5,58
= 5,58
![]() = 7,06
= 7,06
У всіх випадках використовують ряди з одночасним періодом спостережень.
Знаходимо за формулою (3) всі недостаючі дані, вивчаючої річки в роки, коли не було спостережень.
Q1976 = 10,3 + 0,95 * 0,79 * (21,0 - 13,7) = 15,78
Q1977 = 10,3 + 0,95 * 0,79 * (24,7 - 13,7) = 18,56
Q1978 = 10,3 + 0,95 * 0,79 * (17,7- 13,7) = 13,3
Q1979 = 10,3 + 0,95 * 0,79 * (9,6- 13,7) = 7,22
Q1980 = 10,3 + 0,95 * 0,79 * (13,7 - 13,7) = 10,3
Q1991 = 10,3 + 0,95 * 0,79 * (8,8 - 13,7) = 6,62
Одержавши тим самим довгий ряд, знаходять норму стоку за формулою (2).
2.2 Визначення коефіцієнтів варіації та асиметрії
Для порівняння мінливості окремих рядів, які відрізняються своїми значеннями, використовуються коефіцієнти варіації (Сн ), яки визначаємося за формулою:
![]()
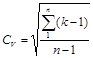 =
= ![]() = 0,5 (7)
= 0,5 (7)
де К - модульний коефіцієнт, який являє собою відношення Qi /Qcp .
Ряд є симетричним, коли додатні і від’ємні відхилення від середнього арифметичного (Qi – Qcp ), повторюються однаково часто, тобто симетрично групуються відносно центру розподілу.
В тих випадках, коли додатні або від’ємні відхилення повторюються часто або рідко, ряд асиметричний. Асиметричність ряду характеризуються коефіцієнтом асиметрії, який визначається за формулою:
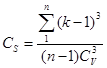 =
= ![]() = 0,5 (8)
= 0,5 (8)
Для визначення значень Сv i Cs беремо продовжуваний ряд заданої річки, а розрахунки заносимо в табл.2.
Розрахунок параметрів для визначення Сv i Cs
| Роки | Q, м3 /c | Qi К = Qcp |
К – 1 |
(К – 1)2 |
(К – 1)3 |
| 1961 | 5,4 | 0,54 | -0,46 | 0,212 | -0,097 |
| 1962 | 18,6 | 1,86 | 0,86 | 0,740 | 0,636 |
| 1963 | 4,7 | 0,47 | -0,53 | 0,281 | -0,149 |
| 1964 | 5,1 | 0,51 | -0,49 | 0,240 | -0,118 |
| 1965 | 6,0 | 0,6 | -0,4 | 0,160 | -0,064 |
| 1966 | 12,3 | 1,23 | 0,23 | 0,053 | 0,012 |
| 1967 | 10,4 | 1,04 | 0,04 | 0,002 | 0,001 |
| 1968 | 13,6 | 1,36 | 0,36 | 0,130 | 0,047 |
| 1969 | 14,9 | 1,49 | 0,49 | 0,240 | 0,118 |
| 1970 | 19,6 | 1,96 | 0,96 | 0,922 | 0,885 |
| 1971 | 17,5 | 1,75 | 0,75 | 0,563 | 0,422 |
| 1972 | 6,1 | 0,61 | -0,39 | 0,152 | -0,059 |
| 1973 | 5,9 | 0,59 | -0,41 | 0,168 | -0,069 |
| 1974 | 4,0 | 0,4 | -0,6 | 0,360 | -0,216 |
| 1975 | 6,4 | 0,64 | -0,36 | 0,130 | -0,047 |
| 1976 | 15,78 | 1,58 | 0,58 | 0,334 | 0,1931 |
| 1977 | 18,56 | 1,86 | 0,86 | 0,733 | 0,6272 |
| 1978 | 13,3 | 1,33 | 0,33 | 0,109 | 0,0359 |
| 1979 | 7,22 | 0,72 | -0,28 | 0,077 | -0,0215 |
| 1980 | 10,3 | 1,03 | 0,03 | 0,001 | 0,0000 |
| 1981 | 6,62 | 0,66 | -0,34 | 0,114 | -0,0386 |
| 1982 | 4,7 | 0,47 | -0,53 | 0,281 | -0,1489 |
| 1983 | 4,0 | 0,40 | -0,60 | 0,360 | -0,2160 |
| 1984 | 5,3 | 0,53 | -0,47 | 0,221 | -0,1038 |
| 1985 | 7,1 | 0,71 | -0,29 | 0,084 | -0,0244 |
| 1986 | 6,0 | 0,60 | -0,40 | 0,160 | -0,0640 |
| 1987 | 7,4 | 0,74 | -0,26 | 0,068 | -0,0176 |
| 1988 | 8,9 | 0,89 | -0,11 | 0,012 | -0,0013 |
| 1989 | 15,6 | 1,56 | 0,56 | 0,314 | 0,1756 |
| 1990 | 19,3 | 1,93 | 0,93 | 0,865 | 0,8044 |
| 1991 | 7,4 | 0,74 | -0,26 | 0,068 | -0,0176 |
| 1992 | 12,5 | 1,25 | 0,25 | 0,063 | 0,0156 |
| 1993 | 15,1 | 1,51 | 0,51 | 0,260 | 0,1327 |
| 1994 | 9,8 | 0,98 | -0,02 | 0,001 | 0,0000 |
| 1995 | 4,7 | 0,47 | -0,53 | 0,2809 | 0,1489 |
| S | 10,02 |
2.3 Забезпеченість, її визначення і будова кривої забезпеченості при обмежений кількості даних
Всі гідротехнічні споруди розраховуються на певну забезпеченість. Якщо розташувати ряд в убиваючому порядку, то під забезпеченістю будь-якої величини цього ряду розуміється імовірність перевищування даного значення і більше нього серед сукупності всіх можливих значень. Є декілька способів визначення забезпеченості. Вибір кожного з них, в основному, залежить від довжини ряду спостережень. Спочатку ми використовуємо спосіб визначення забезпеченості при наявності короткого 30-40 річного ряду.
Цей спосіб заключається в слідуючому. Члени хронологічного ряду спостережень за “n” років розташовують в убиваючому порядку з наданням кожному числу порядкового номера “m”, який змінюється від 1 до “n”.
Для кожного значення розраховують імовірність перевищування серед сукупності всіх значень, що маємо в ряду, за допомогою формули
m
Рm = ------- · 100, % (9)
n + 1
Наносячи на графік точки з координатами (Рm і Qm ), та усереднюючи їх на око, одержують криву забезпеченості гідрологічної характеристики, що розглядається
Всі розрахунки зводжу у табл.3.
Розрахунок емпіричної кривої забезпеченості
| Роки | Q, м3 /с | Q в убиваючому порядку, м3 /с |
M | Qm К =------ Qср |
m P =------100,% N + 1 |
| 1961 | 5,4 | 19,6 | 1 | 1,96 | 2,7 |
| 1962 | 18,6 | 19,3 | 2 | 1,93 | 5,5 |
| 1963 | 4,7 | 18,6 | 3 | 1,86 | 8,3 |
| 1964 | 5,1 | 18,56 | 4 | 1,856 | 11,1 |
| 1965 | 6,0 | 17,5 | 5 | 1,75 | 13,8 |
| 1966 | 12,3 | 15,78 | 6 | 1,578 | 16,6 |
| 1967 | 10,4 | 15,6 | 7 | 1,56 | 19,4 |
| 1968 | 13,6 | 15,1 | 8 | 1,51 | 22,2 |
| 1969 | 14,9 | 14,9 | 9 | 1,49 | 25,0 |
| 1970 | 19,6 | 13,6 | 10 | 1,36 | 27,7 |
| 1971 | 17,5 | 13,3 | 11 | 1,33 | 30,5 |
| 1972 | 6,1 | 12,5 | 12 | 1,25 | 3,33 |
| 1973 | 5,9 | 12,3 | 13 | 1,23 | 36,1 |
| 1974 | 4,0 | 10,4 | 14 | 1,04 | 38,8 |
| 1975 | 6,4 | 10,3 | 15 | 1,03 | 41,6 |
| 1976 | 15,78 | 9,8 | 16 | 0,98 | 44,4 |
| 1977 | 18,56 | 8,9 | 17 | 0,89 | 47,2 |
| 1978 | 13,3 | 7,4 | 18 | 0,74 | 50,0 |
| 1979 | 7,22 | 7,4 | 19 | 0,74 | 52,7 |
| 1980 | 10,3 | 7,22 | 20 | 0,722 | 55,5 |
| 1981 | 6,62 | 7,1 | 21 | 0,71 | 58,3 |
| 1982 | 4,7 | 6,62 | 22 | 0,662 | 61,1 |
| 1983 | 4,0 | 6,4 | 23 | 0,64 | 63,8 |
| 1984 | 5,3 | 6,1 | 24 | 0,61 | 66,6 |
| 1985 | 7,1 | 6 | 25 | 0,6 | 65,4 |
| 1986 | 6,0 | 6 | 26 | 0,6 | 72,2 |
| 1987 | 7,4 | 5,9 | 27 | 0,59 | 75,0 |
| 1988 | 8,9 | 5,4 | 28 | 0,54 | 77,7 |
| 1989 | 15,6 | 5,3 | 29 | 0,53 | 80,5 |
| 1990 | 19,3 | 5,1 | 30 | 0,51 | 83,3 |
| 1991 | 7,4 | 4,7 | 31 | 0,47 | 86,1 |
| 1992 | 12,5 | 4,7 | 32 | 0,47 | 88,8 |
| 1993 | 15,1 | 4,7 | 33 | 0,47 | 91,6 |
| 1994 | 9,8 | 4 | 34 | 0,4 | 94,4 |
| 1995 | 4,7 | 4 | 35 | 0,4 | 97,2 |
2.4 Побудова аналітичної кривої забезпеченості
Аналітичну криву забезпеченості будують, а частіше добудовують, при обмежувальному числі даних спостережень, коли емпірична крива забезпеченості слабо або зовсім на дає можливості визначити Q або К на кінцевих ділянках, які відносяться до області великих і малих значень стоку.
Аналітичні криві забезпеченості будують при відомих параметрах Q (Qср ), Сн , і Сs за допомогою таблиць трьохпараметричного гамма або біномального розподілу.
В таблиці біномального розподілу приводяться нормовані відхилення модульних коефіцієнтів КР% від одиниці (тобто від середнього значення) які виражені в частках коефіцієнта варіації в залежності від забезпеченості при фіксованих коефіцієнтах асиметрії. Ці відхилення називаються числами Фостера і визначаємося за формулою:
КР% - 1
ФР% = ---------- (10)
Сн
З формули (10) можна записати
КР% = ФР% Сн + 1 (11)
Тоді витрати завданої забезпеченості, в свою чергу, визначаємося як
QР% = Кр% Q = (ФР% Сн + 1) Q (12)
У подальшому порядок побудови кривої забезпеченості аналогічний попередньому параграфу.
Для побудови цієї кривої забезпеченості необхідно скористатися величинами Qср , Сн , Сs , які одержані в підрозділах 3.1 і 3.2 і додатком, в якому приведені числа Фостера. Всі розрахунки зводжу в таблицю 4.
Визначення теоретичних значень
| Р, % | 0,01 | 0,1 | 5 | 10 | 25 | |||||||
| Фр% | 4,63 | 3,81 | 1,77 | 1,32 | 0,62 | |||||||
| КР% | 3,32 | 2,91 | 1,89 | 1,66 | 1,31 | |||||||
| QР% | 33,27 | 29,16 | 18,94 | 16,63 | 13,13 | |||||||
| К, % | 50 | 75 | 90 | 95 | 99 | 99,9 | ||||||
| ФР% | -0,08 | -0,71 | -1,22 | -1,49 | 1,96 | -2,4 | ||||||
| КР% | 0,96 | 0,65 | 0,39 | 0,26 | 0,02 | -0,2 | ||||||
| QР% | 9,62 | 6,51 | 3,9 | 2,61 | 0,21 | -2,0 | ||||||
2.5 Побудова кривих повторюваності і забезпеченості при достатній кількості даних
Цей спосіб застосовується при великому об’ємі спостережень (більше 50 років). Криві повторюваності і забезпеченості будують за згрупованими даними. Для цього всю амплітуду коливань випадкової величини А = Qmax - Qmin (різниця між максимальними і мінімальними величинами в ряду спостерігаючої величини) ділять на інтервали, або розряди ДQ, і підраховують, скільки значень потрапило в кожний з них, тобто визначаємо абсолютну частоту ni .
Число інтервалів С призначають від 10 до 15 в залежності від числа спостережень N, таким чином, щоб відобразити основні риси розглядаючої статистичної сукупності. Інтервали ДQ призначають однаковими. За їх величини приймають таке число, щоб після ділення А/С не лишалось залишку.
Відібрані інтервали не повинні перекриватися, щоб сусідні значення спадаючого ряду не потрапили в суміжні інтервали Контролем при підрахунку абсолютних частот по розрядам є очевидна рівність
∑ni = Н (13)
Для кожного інтервалу розраховують відносну частоту
ni
mi = ----- (14)
N
При цьому, ураховуючи формулу (14) одержують
∑mi = 1 (15)
Всі розрахунки зводжу в таблицю 5.
Емпіричній розподіл середньорічних витрат води
| №№ інтервалу | ДQ, м3 /с | Частота | Накопичена відносна частота Уmi | |
| Абсолютна ni | Відносна, mi | |||
| 1 | 198 – 189 | 1 | 0,021 | 0,021 |
| 2 | 188 – 179 | 2 | 0,042 | 0,063 |
| 3 | 178 – 169 | 3 | 0,063 | 0,1255 |
| 4 | 168 – 159 | 3 | 0,063 | 0,188 |
| 5 | 158 – 149 | 3 | 0,063 | 0,2505 |
| 6 | 148 – 139 | 7 | 0,146 | 0,3965 |
| 7 | 138 – 129 | 8 | 0,167 | 0,5635 |
| 8 | 128 – 119 | 7 | 0,146 | 0,7095 |
| 9 | 118 – 99 | 11 | 0,229 | 0,9385 |
| 10 | 98 – 89 | 1 | 0,021 | 0,9595 |
| 11 | 88 – 79 | 1 | 0,021 | 0,9805 |
| 12 | 78 – 69 | 1 | 0,021 | 1,0000 |
| У | 48 | 1,0000 | 1,0000 | |
Графік розподілу відносних частот за інтервалом називається гістограмою розподілу, яка перетворюється в криву розподілу, якщо маємо нескінченне число членів ряду, а інтервал зменшуємо до нескінченно малої величини. Цей графік показує найбільш характерні риси розподілу: загальну форму розподілу, інтервал найбільших частот, характер асиметрії.
Гістограму будую таким чином. Після всіх розрахунків і заповнення таблиці 5 на міліметровому папері в обраному масштабі по осі ординат відкладаю нижні границі інтервалів ДQi , а по осі абсцис – відносні частоти mi . В результаті одержую сім’ю з’єднаних прямокутників. Це і є ступеневий графік розподілу, або гістограма.
На цьому ж графіку за даними кінцевої графи табл.5 креслю також емпіричну криву забезпеченості середньорічних витрат води. Накопичені відносні частоти Уmi відповідають нижнім границям інтервалів.
3. Регулювання стоку
Основним завданням регулювання стоку є комплексна акумуляція вод весняного або зливового стоку для потреб водопостачання, зрошення, рибальства та інших галузей народного господарства.
Є різні способи регулювання. Найчастіше застосовується сезонне регулювання, коли надлишкова вода весняної повені або літньо-осінього паводка затримується за допомогою водосховища або ставка (водосховище об’ємом до 1 млн.м3), а потім витрачається влітній період на різні цілі.
Для визначення об’ємів будівельних робіт і забезпечення потреб користувачів у воді виконуються водогосподарські розрахунки. Починаються вони з розрахунків притоку води до водосховища.
3.1 Визначення місця розташування і притоку воді до водосховища
Водосховище треба розташувати так, щоб при значній його місткості вартість будівництва була мінімальною. Крім того, як можна менше затоплювались орні землі, береги водосховища повинні бути стійкими, вода з населених пунктів, цвинтарів, скотомогильників не потрапляла б в водосховище. Так як водосховище утворюється затриманням води за допомогою греблі, то вона повинна розташовуватися в найбільш звуженої частині русла річки. Крім того важливо мати також більшу водозбірну площу, від якої залежить об’єм притоку. Об’єм притоку можу бути визначений за формулою:
QT
V = --------- м3 (16)
1000
де Q – норма стоку, м3 /с; Т – кількість секунд в році.
![]() =315360000м.
=315360000м.
Так, як V = f(F) то від розташування греблі по довжині русла річки та від місця розташування водосховища залежить забезпеченість водою всіх потреб користувачів.
3.2 Складові частини водосховища
Кожне водосховище складається з трьох частин. Починаючи з низу вони розташовуються в такому порядку: мертвий, корисний і форсований об’єми.
3.2.1 Мертвий об’єм
Мертвий об’єм (VМО ) це, в основному, місткість для розташування мулу. Він протягом тривалого періоду (50-100 років) замулюється повністю. Тому в водогосподарських розрахунках він не враховується, а всі водозабірні і водоскидні споруди розташовуються вище горизонту МО.
Виходячи з такого положення, мертвий об’єм слід визначати за формулою Є.О.Замаріна, яка дозволяє вирахувати кількість мулу (Wмо ), який надійде з водозбірної площі за певний період часу (50 – 100 років)
![]() =
=![]() = 64248109 (17)
= 64248109 (17)
Де J – уклон річки; V – річної об’єм притоку до водосховища, м3 ; Т – 100-річний період експлуатації водосховища (100 років – це Т = 1); а і в – коефіцієнти, які залежать від площі і еродованості басейну (табл.6, 7); с – коефіцієнт, який залежить від ступеню зарегулювання стоку (табл.8); г – питома вага мулу, що відклався в МО, т/м3 – цей параметр визначається за допомогою формули (18) і таблиці 9.
А
г = ______ + С Т + В (18)
L
г![]()
Де L – відсоток органічних речовин у відкладаннях мулу (5-20%).
Корисний об’єм (КО) представляє собою об’єм всіх витрат, за винятком санітарної витрати. Корисний об’єм розташовується вище мертвого об’єму VМО . Цей об’єм протягом року змінюється від нуля до VКО . Тобто, водосховище то наповнюється, то випорожнюється.
Значення коефіцієнта а
| Характеристика схилів і прилеглої частини басейну | Суглинок, ліс | Глина | Пісок |
| Річка з широкою заболоченою заплавою, плоска рівнина | 1 | 0,7 | 0,5 |
| Схили, зарослі лісом і чагарником, задерновані | 3 | 2 | 1 |
| Те ж, схили круті | 6 | 5 | 4 |
| Схили пологі, відкрити, розорані | 10 | 8 | 6 |
| Схили круті, розорані | 15 | 13 | 10 |
Значення коефіцієнта в
| Характеристика схилів і прилеглої частини басейну | Суглинок | Глина | Пісок |
| Відсутність глибинної ерозії | 1 | 1 | 1 |
| Вибої, канави, вимоїни | 2 | 1,5 | 1,2 |
| Слабо розгалужені яри з неглибоким заляганням базису ерозії | 6 | 4 | 2,5 |
Значення коефіцієнта с
| Ступень зарегулювання стоку | Значення коефіцієнта с |
| 0 | 1 |
| 0,1 | 0,85 |
| 0,1 –0,2 | 0,75 |
| 0,2 - 0,3 | 0,50 |
| 0,3 – 0,4 | 0,40 |
| 0,5 | 0,30 |
Значення параметрів А, В, С
| Найменування грунтів | А | В | С |
| Піщані | 2,30 | 0,25 | 0,0020 |
| Суглинки і леси | 2,00 | 0,45 | 0,0070 |
| Глинисті важкі | 2,25 | 0,35 | 0,0041 |
Після визначення об’єму припливу мулу треба розташувати його в чаші водосховища. Порядок розміщення слідуючий. Спочатку в ніжній частині водосховища в найбільш звуженої частині перпендикулярно напрямку потоку в річці проводиться ось греблі. Починаючи з самої ніжний горизонталі, розташованої вище осі, виконується розрахунок об’ємів прострів між двома cусідніми горизонталями за формулою
F1 + F2
V0 = Дh, м (19)
2
де F1 іF2 – площі оконтурені горизонталями і віссю греблі,м2 ; Дh – відстань по висоті між двома розрахунковими горизонталями.
Ураховуючи, що між нижньою горизонталлю і ложем водосховища залишається ще невеличкий простір, то Дh в даному випадку можна прийняти 0,5 – 1,5 м і при визначенні об’єму V0 за формулою (19) F1 слід прийняти рівною нулю.
Після додавання V0 i V1 ця сума повинна дорівнювати або бути більша, ніж WМО .
У випадку (V0
+ V1
) < Wмо, рахується об’єм між вище розташованими горизонталями і додається до суши V0
29-04-2015, 00:34
