ДЕПАРТАМЕНТ ВЫСШИХ УЧЕБНЫХ ЗАВЕДЕНИЙ
Волгоградская государственная сельскохозяйственная академия
Кафедра: _____________________
Дисциплина: Гидрология
КОНТРОЛЬНАЯ РАБОТА
Выполнила: студент третьего курса,
заочного отделения, группы __ ЭМЗ, _____
________________________________
Волгоград 2006г.
ВАРИАНТ 0 Река Сура, с. Кадышево, площадь водосбора F=27 900 км2 , залесенность 30%, болот нет, среднее многолетнее количество осадков 682 мм.
Среднемесячные и среднегодовые расходы воды и модули стока
| Годы |
Январь |
Февраль |
Март |
Апрель |
Май |
Июнь |
Июль |
Август |
Сентябрь |
Октябрь |
Ноябрь |
Декабрь |
Год |
М л/с*км2 |
Ма л/с*км2 |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| 1964 |
47,6 |
42,6 |
44,9 |
699 |
259 |
94,7 |
66,8 |
60,8 |
51,0 |
49,7 |
44,3 |
42,5 |
125 |
4,48 |
4,23 |
| 1965 |
37,9 |
41,2 |
56,1 |
574 |
148 |
71,4 |
53,3 |
50,1 |
46,8 |
48,4 |
45,1 |
55,2 |
102 |
3,66 |
3,54 |
| 1966 |
46,4 |
42,9 |
141 |
380 |
85,5 |
55,6 |
47,6 |
42,2 |
42,3 |
43,1 |
43,9 |
37,2 |
83,9 |
3,01 |
2,66 |
| 1967 |
27,6 |
33,2 |
36,3 |
332 |
94,6 |
53,9 |
44,4 |
46,1 |
38,4 |
40,4 |
36,9 |
31,4 |
67,9 |
2,43 |
2,47 |
| 1968 |
32,8 |
27,2 |
48,9 |
767 |
113 |
72,1 |
79,0 |
45,3 |
42,2 |
45,2 |
51,8 |
15,4 |
112 |
4,01 |
3,72 |
| 1969 |
27,4 |
23,0 |
20,0 |
636 |
104 |
68,1 |
67,4 |
52,4 |
45,5 |
64,9 |
76,8 |
73,7 |
105 |
3,76 |
2,42 |
| 1970 |
54,5 |
55,1 |
48,8 |
1120 |
137 |
77,5 |
54,7 |
48,1 |
48,9 |
52,3 |
66,2 |
44,7 |
151 |
5,41 |
4,24 |
| 1971 |
43,8 |
40,3 |
95,6 |
565 |
104 |
58,6 |
51,8 |
42,0 |
36,7 |
48,4 |
60,1 |
63,4 |
101 |
3,62 |
2,88 |
| 1972 |
32,7 |
26,4 |
48,6 |
333 |
67,4 |
51,2 |
44,6 |
26,2 |
27,4 |
37,2 |
48,1 |
60,6 |
67,0 |
2,40 |
1,71 |
| 1973 |
34,3 |
32,0 |
37,3 |
308 |
86,4 |
56,6 |
56,1 |
66,2 |
57,8 |
66,9 |
94,4 |
67,9 |
79,5 |
2,85 |
2,40 |
Бассейн – аналог – р. Сура, г. Пенза.
Средняя многолетняя величина годового стока (норма) Моа =3,5 л/с*км2 , Сv = 0,27.
Таблица для определения параметров при подсчете максимального расхода талых вод
| Вариант |
Река-пункт |
F1 |
ko |
n1 |
h |
Cv |
|
n2 |
|
| 0 |
Сура-Кадышево |
2 |
0,020 |
0,25 |
80 |
0,40 |
1,30 |
0,20 |
0,8 |
1. Определить среднюю многолетнюю величину (норму) годового стока при наличии данных наблюдений.
Исходные данные: среднегодовые расходы воды, рассчитываемый период 10 лет (с 1964 – 1973 гг.).
Qо
=![]() ,
,
где Qi – средний годовой стока за i-й год;
n – число лет наблюдений.
Qi =994,3
Qо= ![]() =
99,43 м3
/с (величина среднего многолетнего стока).
=
99,43 м3
/с (величина среднего многолетнего стока).
Полученную норму в виде среднего многолетнего расхода воды требуется выразить через другие характеристики стока: модуль, слой, объем и коэффициент стока.
Модуль стока Мо
=![]() =
= ![]() =3,56 л/с*км2
, где F – площадь водосбора, км2
.
=3,56 л/с*км2
, где F – площадь водосбора, км2
.
Средний многолетний объем стока за год:
Wo =Qo * T=99,43*31,54*106 =3 136,022 м3 ,
где Т – число секунд в году, равное приблизительно 31,54*106 с.
Средний многолетний слой стока ho
=![]() =
=![]() =112,4мм/год
=112,4мм/год
Коэффициент стока α=![]() =
=![]() =0,165,
=0,165,
где хо – средняя многолетняя величина осадков в год, мм.
2. Определить коэффициент изменчивости (вариации) С v годового стока.
Сv
=![]() ,
где
,
где![]() –
среднеквадратическое отклонение годовых расходов от нормы стока.
–
среднеквадратическое отклонение годовых расходов от нормы стока.
![]() =
=  .
.
Если n<30, то ![]() =
= 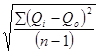 .
.
Если сток за отдельные годы выразить в виде модульных коэффициентов к=![]() , то Сv
=
, то Сv
=![]() , а при n<30 Сv
=
, а при n<30 Сv
=
![]() Составим таблицу для подсчета Сv
годового стока реки.
Составим таблицу для подсчета Сv
годового стока реки.
Таблица 1
![]() Данные для подсчета Сv
Данные для подсчета Сv
| № п/п |
Годы |
Годовые расходы м3 /с |
Qo |
к= |
К-1 |
(к-1)2 |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 1 |
1964 |
125,00 |
99,43 |
1,26 |
0,26 |
0,066 |
| 2 |
1965 |
102,00 |
99,43 |
1,03 |
0,03 |
0,001 |
| 3 |
1966 |
83,90 |
99,43 |
0,84 |
-0,16 |
0,024 |
| 4 |
1967 |
67,90 |
99,43 |
0,68 |
-0,32 |
0,101 |
| 5 |
1968 |
112,00 |
99,43 |
1,13 |
0,13 |
0,016 |
| 6 |
1969 |
105,00 |
99,43 |
1,06 |
0,06 |
0,003 |
| 7 |
1970 |
151,00 |
99,43 |
1,52 |
0,52 |
0,269 |
| 8 |
1971 |
101,00 |
99,43 |
1,02 |
0,02 |
0,000 |
| 9 |
1972 |
67,00 |
99,43 |
0,67 |
-0,33 |
0,106 |
| 10 |
1973 |
79,50 |
99,43 |
0,80 |
-0,20 |
0,040 |
| Всего: |
994,30 |
10,00 |
0,00 |
0,627 |
||
Сv
= =
=![]() =
= ![]() = 0.2638783=0.264.
= 0.2638783=0.264.
Относительная средняя квадратическая ошибка средней многолетней величины годового стока реки за период с 1964 по 1973 гг. (10 лет) равна:
![]() =
= ![]() =
=![]() = 8,3%
= 8,3%
Относительная средняя квадратическая ошибка коэффициента изменчивости Сv при его определении методом моментов равна:
![]() =23,24%.
=23,24%.
Длина ряда считается достаточной для определения Qo
и Cv
, если ![]()
![]() 5-10%, а
5-10%, а ![]() 10-15%. Величина среднего годового стока при этом условии называется нормой стока. В нашем случае
10-15%. Величина среднего годового стока при этом условии называется нормой стока. В нашем случае ![]() находится в пределах допустимого, а
находится в пределах допустимого, а ![]() больше допустимой ошибки. Значит, ряд наблюдений недостаточный необходимо удлинить его.
больше допустимой ошибки. Значит, ряд наблюдений недостаточный необходимо удлинить его.
3. Определить норму стока при недостатке данных методом гидрологической аналогии.
Река-аналог выбирается по:
– сходству климатических характеристик;
– синхронности колебаний стока во времени;
– однородности рельефа, почвогрунтов, гидрогеологических условий, близкой степени покрытости водосбора лесами и болотами;
– соотношению площадей водосборов, которые не должны отличаться более чем в 10 раз;
– отсутствию факторов, искажающих сток (строительство плотин, изъятие и сброс воды).
Река-аналог должна иметь многолетний период гидрометрических наблюдений для точного определения нормы стока и не менее 6 лет параллельных наблюдений с изучаемой рекой.

По графику связи Мо равно 7,9 л/с.км2
QO
=![]() =
= ![]() =106,02
=106,02
Коэффициент изменчивости годового стока:
Сv
=A![]() Cva
,
Cva
,
где Сv – коэффициент изменчивости стока в расчетном створе;
Cva – в створе реки-аналога;
Моа – среднемноголетняя величина годового стока реки-аналога;
А – тангенс угла наклона графика связи.
В нашем случае:
Сv =1*3,5/3,8*0,27=0,25
Окончательно принимаем Мо =3,8 л/с*км2 , QO =106,02 м3 /с, Сv =0,25.
4. Построить и проверить кривую обеспеченности годового стока.
В работе требуется построить кривую обеспеченности годового стока, воспользовавшись кривой трехпараметрического гамма-распределения. Для этого необходимо рассчитать три параметра: Qo – среднюю многолетнюю величину (норму) годового стока, Cv и Cs годового стока.
Используя результаты расчетов первой части работы для р. Сура, имеем QO =106,02 м3 /с, Сv =0,25.
Для р. Сура принимаем Cs =2Сv =0,50 с последующей проверкой.
Ординаты кривой определяем в зависимости от коэффициента Сv по таблицам, составленным С.Н. Крицким и М.Ф. Менкелем для Cs =2Сv . Для повышения точности кривой необходимо учитывать сотые доли Сv и провести интерполяцию между соседними столбцами цифр.
Ординаты теоретической кривой обеспеченности среднегодовых расходов воды реки Сура с. Кадышево.
Таблица 2
| Обеспеченность, Р% |
0,01 |
0,1 |
1 |
5 |
10 |
25 |
50 |
75 |
90 |
95 |
99 |
99,9 |
| Ординаты кривой |
2,22 |
1,96 |
1,67 |
1,45 |
1,33 |
1,16 |
0,98 |
0,82 |
0,69 |
0,59 |
0,51 |
– |
ГРАФИК
Построить кривую обеспеченности на клетчатке вероятностей и проверить ее данные фактических наблюдений.

Таблица 3
Данные для проверки теоретической кривой
| № п/п |
Модульные коэффициенты по убыванию К |
Фактическая обеспеченность Р = |
Годы, соответствующие К |
| 1 |
1,52 |
9,09 |
1970 |
| 2 |
1,26 |
18,18 |
1964 |
| 3 |
1,13 |
27,27 |
1968 |
| 4 |
1,06 |
36,36 |
1969 |
| 5 |
1,03 |
45,45 |
1965 |
| 6 |
1,02 |
54,55 |
1971 |
| 7 |
0,84 |
63,64 |
1966 |
| 8 |
0,80 |
72,73 |
1973 |
| 9 |
0,68 |
81,82 |
1967 |
| 10 |
0,67 |
90,91 |
1972 |
Для этого модульные коэффициенты годовых расходов нужно расположить по убыванию и для каждого из них вычислить его фактическую обеспеченность по формуле Р =![]() , где Р – обеспеченность члена ряда, расположенного в порядке убывания;
, где Р – обеспеченность члена ряда, расположенного в порядке убывания;
m – порядковый номер члена ряда;
n – число членов ряда.
Как видно из последнего графика, нанесенные точки осредняют теоретическую кривую, значит кривая построена правильно и соотношение Cs =2 Сv соответствует действительности.
5. Рассчитать внутригодовое распределение стока методом компоновки для целей орошения с расчетной вероятностью превышения Р=80%.
Расчет делится на две части:
а) межсезонное распределение, имеющее наиболее важное значение;
б) внутрисезонное распределение (по месяцам и декадам), устанавливаемое с некоторой схематизацией.
Расчет выполняется по гидрологическим годам, т.е. по годам, начинающимся с многоводного сезона. Сроки сезонов начинаются едиными для всех лет наблюдений с округлением их до целого месяца. Продолжительность многоводного сезона назначается так, чтобы в границах сезона помещалось половодье как в годы с наиболее ранним сроком наступления, так и с наиболее поздним сроком окончания.
В задании продолжительность сезона можно принять следующий: весна-апрель, май, июнь; лето-осень – июль, август, сентябрь, октябрь, ноябрь; зима – декабрь и январь, февраль, март следующего года.
Величина стока за отдельные сезоны и периоды определяется суммой среднемесячных расходов. В последнем году к расходу за декабрь прибавляются расходы за 3 месяца (I, II, III) первого года.
| Расчет внутригодового распределения стока методом компоновки (межсезонное распределение). р. Сура за 1964 – 1973 гг. |
||||||||||||||||
| № п/п |
Годы |
Расходы за лимитирующий сезон лето-осень |
∑ сток лето-осень |
Среднее значение стока лето-осень 29-04-2015, 01:00 Разделы сайта | ||||||||||||
