Метод волновых фронтов (полей времен)
а) Метод Торнберга. Целый ряд способов интерпретации данных МПВ, как правило графических, основан на реконструкции волновых фронтов.
Рис. 7 иллюстрирует принцип метода построения волновых фронтов. Фронт преломленной волны, достигающий точки А в момент времени t = 1,600 с, подходит к В, С, ... в моменты 1,600 + D tB , 1,600 + D tc , .... Построив дуги окружностей с центрами В, С, ... и радиусами V 1 D tB , V 1 D tC ,,… , мы можем восстановить волновой фронт для t = 1,600 с ( AZ ) с требуемой точностью. Подобным же образом можно построить волновые фронты для любого момента времени (см., например, приведенный на том же рисунке волновой фронт для t = 1,400 с) Показаны также волновые фронты прямой волны от источника S , являющиеся окружностями.
На рис. 8 изображены только те фронты, которые соответствуют волнам, приходящим первыми (все последующие вступления для простоты исключены из рассмотрения). В интервале между источником S и точкой выхода преломленной волны С в первых вступлениях наблюдается прямая волна. Вправо от С первой приходит волна, преломленная на первой границе, но вправо от G ее обгоняет волна, преломленная на более глубокой границе.
Две системы волновых фронтов, соответствующие прямой волне и волне, преломленной на первой границе, пересекаются
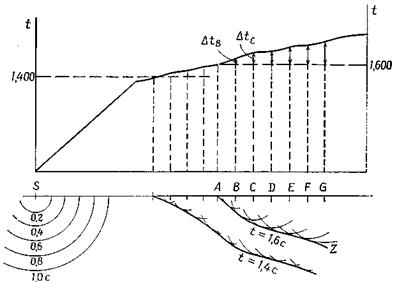
Рис. 7. Построение волновых фронтов.
вдоль пунктирной линии ABC ; эта линия, названная Торнбергом кривой совпадения времен, проходит через точки, где пересекающиеся волновые фронты характеризуются одинаковым временем. DEFG — кривая совпадения времен для более глубокой границы. Кривые совпадения времен касаются преломляющих границ в точках А и D , где угол падения луча достигает критического значения, а точки, в которых кривые совпадения времен пересекают поверхность, отличаются резким изменением наклона годографа.
Поскольку кривая совпадения времен касается преломляющей границы, положение последней можно найти, если есть данные по одному профилю плюс некоторые дополнительные данные, например ее наклон, глубина, критический угол, или же данные еще по одному профилю (не обязательно встречному), так как в этом случае есть две кривые совпадения времен и преломляющая граница является для них общей касательной.
Если есть данные по встречным профилям, построение волновых фронтов позволяет реализовать изящный метод построения преломляющей границы. Суть метода ясна из рис. 9,
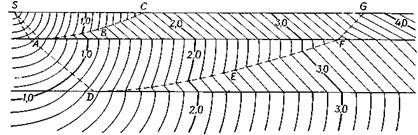
Рис. 9.Кривые совпадения времен.
на котором показаны два волновых фронта MCD и РСЕ, построенных из точек А и В и пересекающихся в промежуточной точке С. Очевидно, что сумма времен пробега от А и В до С равна взаимному времени tr для пунктов взрыва А и В. Если построить два волновых фронта по годографу, не зная положения преломляющей границы RS , они будут выглядеть как MCN
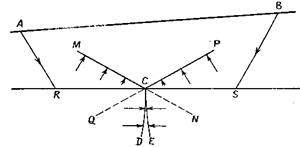
Рис. 9.Построение преломляющей границы по точкам пересечения волновых фронтов.
и PCQ , а не как MCD и РСЕ. Следовательно, если начертить пары волновых фронтов из А и В, таких, что сумма времен пробега равна tr , преломляющая граница будет проходить через точки пересечения соответствующих пар волновых фронтов на рис. 9.
б) Метод «плюс-минус» Хагедорна. В методе «плюс-минус» Хагедорна применяется построение, сходное с вышеописанным. Когда преломляющая граница горизонтальна, пересекающиеся волновые фронты, проведенные с интервалом D мс, образуют ромбовидные фигуры (рис. 10), горизонтальные и вертикальные диагонали которых равны V 2 D и V 1 D/cosQ соответственно. Если сложить два значения времени пробега на любом пересечении и вычесть t 0 , то полученный результат (значение «плюс») будет равен нулю на преломляющей границе,
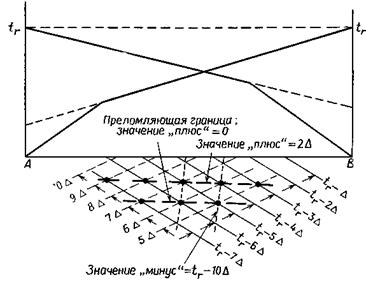
Рис. 10. Интерпретация по методу «плюс-минус:
+2D на горизонтальной прямой, проходящей через предыдущий ряд значений по вертикали над теми пересечениями, которые определяют преломляющую границу, +4D на следующей линии пересечений вверх по разрезу и т. д. Поскольку расстояние между каждой парой соседних линий составляет V 1 D/cosQ, для построения преломляющей границы можно использовать любую из «плюс»-линий. Разность между двумя временами в точке пересечения называется значением «минус»; она постоянна вдоль субвертикальных линий, проходящих через пересечения волновых фронтов. Расстояние между последовательными «минус»-линиями, как следует из рис. 10, составляетV 2 D; благодаря этому можно непрерывно контролировать значение V 2 . Несмотря на то что наклон границы изменяет приведенные соотношения, в случае небольших углов наклона искажения достаточно малы; поэтому считается, что «плюс»-линии остаются параллельными преломляющей границе, а «минус»-линии не сходятся и не расходятся по отношению друг к другу.
в) Графический метод Хейлса. Графические способы очень удобны для решения многих задач интерпретации в методе преломленных волн. При аккуратном выполнении графические построения обычно позволяют быстро получить решение с требуемой точностью, и ими удобно пользоваться, так как интерпретация отличается наглядностью.
Метод Хейлса полезен в тех случаях, когда заметно меняется глубина преломляющей границы; такая ситуация часто связана с изменениями скоростей в покрывающей толще, а также граничных скоростей. Для применения этого метода нужны встречные годографы. Сущность его в использовании сопряженных точек, скажем А и В (рис. 11, а ), расположение которых соответствует общей точке Q отхода волны от границы; при этом глубина и наклон преломляющей границы заранее не известны. Сначала мы опишем процесс интерпретации, а затем докажем сделанные предположения.
На данной паре встречных годографов, подобных приведенным на рис. 11, б , выбираем произвольную точку В, в которой время прихода волны равно tRB . Точка К определяется соотношением KB = tr — tRB . Прямая, проходящая через К под углом a = arctg(V1 sinQ), отсекает на встречном годографе время tSA в положении А, которое является точкой на встречном профиле, связанной с той же точкой на преломляющей границе (Q на рис. 11, а ), что и В. Теперь можно определить время t ’ и расстояние x ’ (рис. 11, б ) по встречному годографу. Проводим прямую через А под критическим углом Q (рис. 11, в ), которая пересекает в точке С перпендикуляр, восстановленный в середине отрезка АВ. Затем проводим дугу радиуса r = V 1 t ’ /2cosQ. Преломляющую границу строим как огибающую дуг, проведенных таким путем. Угол a , введенный выше, не точно равен углу a ', но, как будет показано, этой ошибкой можно пренебречь.
Чтобы доказать провильность построений этого метода, рассмотрим треугольник AQB (рис. 11, г ), где Q — точка преломления. Преломленные волны, распространяющиеся от R до В и от S до А (рис. 11, а ), отходят от преломляющей границы в точке Q . Проведем окружность через точки A , Q и В, после чего значения ряда углов можно выразить через критический угол Q и угол наклона границы x. Расстояние CQ = r можно найти, если учесть, что
![]() .
.
HoAN = CN tgx = CG tgx = BG ; подставив эти значения в выражение для rcosQ, получим
![]() .
.
.
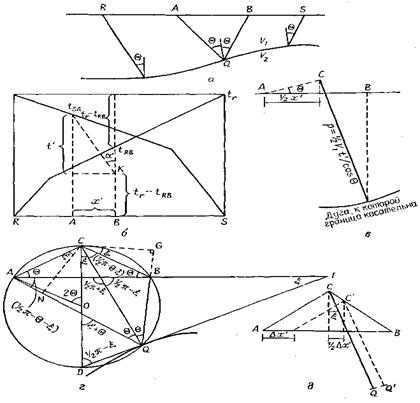
Рис. 11. Графический метод Хейлса. а —две сопряженные точки приема А и В, имеющие общую точку Q отхода волны от границы; б — геометрические свойства точек годографов, соответствующих пунктам приема А и В (вспомогательные линии построений показаны пунктиром); в — геометрические построения для определения точки Q ; г — геометрические свойства окружности, проходящей через точки А, В, Q ; д — влияние ошибки в определении х' в п. б.
Из рис. 11, а ясно, что
![]()
следовательно,
![]()
![]()
Далее,
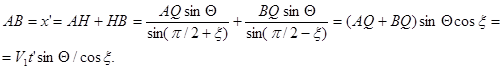
Углы a = arctg(V1 sinQ) и a' = arctg(x ’ /t ’ ) равны, если x = 0. Если x¹ 0, то a' > a, поэтому точка A будет сдвинута в сторону точки В на расстояние D х', tSA и t ’ уменьшатся на величину D t ', ar будет меньше на D r. На основании рис. 11, д , имея в виду, что D t '/ D x ' = наклон годографа = sin (Q+x)/ V 1 (для годографа, полученного по падению границы), запишем:
![]()
Точка С, от которой откладывается расстояние r, также сдвинется в положение С (рис. 11, д ):
![]()
это расстояние равно точно Dr. Следовательно, если сместить точку преломления по восстанию границы на величину D х'/2, можно скомпенсировать влияние, обусловленное наклоном границы.
Метод Хейлса требует знания V 1 и V 2 для вычисления a . Изменения V 2 можно учесть, рассчитывая V 2 по наклонам соответствующих годографов в точках В и А (обычно достаточно аппроксимировать положение А). Изменения V 1 с глубиной (обычно увеличение с ростом глубины) можно учесть путем итеративных расчетов.
Обработка и интерпретация данных МПВ в системе RadExPro
Принципы построения преломляющей границы
При интерпретации данных МПВопределяется положение преломляющей границы и значение граничной скорости (скорости в подстилающей толще, при условии однородности этой толщи).
Скорость в покрывающей толще (средняя скорость) по годографам преломленных волн не определяется. Её значение можно найти по годографу прямой волны
![]() ,
,
или при построении преломляющей границы можно использовать значение средней скорости, полученное по другим данным (MOB, CK). Обычно покрывающая толща предполагается однородной, поэтому, если значение V ср определялось в нескольких точках профиля, то при интерпретации берут осредненное ее значение.
Еслипреломляющая граница горизонтальная, то граничная скорость V Г определяется непосредственно по наклону годографа головной волны
![]()
![]() ,
,
а глубина границы - по точке пересечения продолжения годографа с осью времен (согласно уравнению годографа)
![]() , (8)
, (8)
Однако на практике нужно иметь такой способ, который позволяет строить преломляющую границу при более широких допущениях. Наиболее распространенным является способ ta .
Условия применения его следующие:
1) радиус кривизны преломляющей границы значительно больше глубины ее залегания (граница "достаточно гладкая");
2) граничная скорость изменяется плавно;
3) проникание лучей во вторую среду отсутствует;
4) покрывающая толща однородная, скорость в ней известна.
Причины указанных ограничений будут ясны при выводе основной формулы способа, где можно сделать и их количественную оценку. Построение границы по способу t 0 возможно только на тех участках профиля, где имеется два встречных годографа. Наблюдения должны быть проведены по 4-х точечной системе. Используя нагоняющие годографы, прямой и обратный годографы головной волны можно достроить в «мертвой» зоне. Полученные сводные годографы Г1 и Г2 увязываются между собой во взаимных точках, где время равно Т (рис. 12).
Вывод основной формулы . Времена прихода t 1 и t 2 обеих преломленных волн в произвольную точку наблюдения S ( x ), если учитывать ход лучей на рис. 12 (проницание отсутствует), определяется соотношениями:
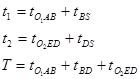
Откуда
![]() (9)
(9)
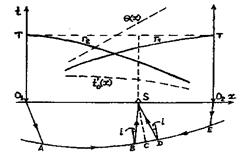
Рис. 12. К выводу основной формулы способа t 0 .
Опустим из точки S перпендикуляр SC на границу R . Принимая во внимание сделанные допущения, получаем
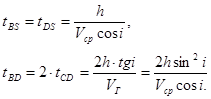
Учитывая далее равенства (8) и (9),
![]() (10)
(10)
Следовательно, если в точке S(x) известны времена t 1 и t 2 по встречным годографам, а также взаимное время Т, то можно вычислить время t 0 (x )в этой точке.
Эхо-глубину h , до преломляющей границы можно записать в виде
![]() ,(11)
,(11)
где 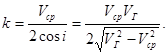
Для вычисления коэффициента k следует предварительно определить граничную скорость V Г . Составим разностный годограф
![]() (12)
(12)
Его угловой коэффициент ![]() с учетом формулы
с учетом формулы
![]()
![]()
для кажущихся скоростей выразим так:
![]() . (13)
. (13)
Отсюда можно определить граничную скорость V Г . Обычно пользуются приближенной формулой, строго верной для горизонтальных границ
![]() (14)
(14)
Если линия Q(х )аппроксимируется одной прямой линией, то получаем одно значение V Г , что говорит о горизонтальной однородности второй толщи. Если же Q(х )прямой линией не аппроксимируется, то можно говорить об изменении свойств подстилающей толщи вдоль профиля, но это может быть обусловлено и ошибками наблюдений или обработки.
После определения V Г вычисляют значение коэффициента k и строят преломляющую границу как огибающую семейства окружностей
При изменении V ср и V Г вдоль профиля, преломляющую границу строят, используя разные значения k для разных участков, в переходной зоне положение границы обычно находят интерполированием. Но здесь могут быть иразрывные нарушения.
Режим КМПВ (Refraction Mode) в системе RadExPro
Программа позволяет, в зависимости от формы годографов, производить их интерпретацию или как годографов головных волн, т.е. строить преломляющие границы, или как годографов рефрагированных волн, т.е. строить изолинии скорости в непрерывной среде с переменной скоростью. Возможна также интерпретация одиночных годографов для приблизительной оценки параметров разреза.
Для перехода в режим КМПВ нужно воспользоваться командой меню Options ® Refraction mode основного окна программы.
П остроение преломляющей границы способом t0. Возможности программы и ограничения
А . Построение одной преломляющей границы
Построение преломляющей границы осуществляется в соответствии с условиями, изложенными в литературе:
1. Построение производится по двум встречным годографам преломленных (головных) волн, полученным по продольным профилям (т.е. источники и приемники находятся на одной прямой);
2. Поверхность наблюдений считается плоской * и горизонтальной *;
3. Преломляющая граница достаточно гладкая, т.е. радиус кривизны границы много больше глубины ее залегания;
4. Проницание волн во вторую среду отсутствует, т.е. преломленная волна «скользит» вдоль границы (головная волна);
5. Покрывающая толща по вертикали представляется однородной средой со средней скоростью V1. Допускается плавное изменение скорости V 1 вдоль профиля **.
6. Граничная скорость (V 2 ) может меняться вдоль профиля скачками * * .
Примечания :
* Рельеф можно учесть двумя способами: 1) ввести статические поправки, чтобы привести наблюдения к горизонтальной плоскости. При окончательном представлении разреза поверхность снова можно показать с рельефом (см. раздел меню «интерпретация»); 2) расчеты можно вести без учета рельефа, а при построении глубины границы можно откладывать от истинного рельефа – это вполне законно, если рельеф представляет собой лишь наклонную площадку.
** Программа RadExPro позволяет определять значения скоростей V 1 и V 2 по годографам волн во всех точках профиля, где размещены источники (см. раздел меню «создание структуры исходных данных»). В последующем можно вручную корректировать эти значения или вводить новые значения (если они известны). В промежуточных точках значения скоростей V 1 интерполируются, значения скоростей V 2 считаются постоянными в интервале до следующей точки задания V 2 . Однако нужно учитывать, что физика преломленных волн и способы вычислений накладывают определенные ограничения на значения скоростей. А именно, при выводе основной формулы способа t 0 считается, что скорости V 1 и V 2 имеют постоянные значения в пределах рассматриваемого треугольника. Определение V 1 по годографу прямой волны и определение V 2 по разностному годографу возможно лишь в предположении постоянства этих скоростей в пределах выбранного интервала. Так что, насколько допустимы изменения этих скоростей вдоль профиля, интерпретатор должен оценивать сам исходя из сейсмогеологических условий и требуемой точности построений.
Б . Построение преломляющей границы по длинным профилям
Построение границы осуществляется для одного интервала наблюдений, т.е. для интервала между двумя пунктами возбуждения, с которых получены встречные годографы. Построение границ для длинных прямолинейных профилей можно осуществить, составляя сводные годографы для крайних пунктов возбуждения путем параллельного переноса годографов головных волн с промежуточных пунктов возбуждения, и соответственно удлиняя интервал наблюдений. Затем система из двух сводных годографов интерпретируется в едином интервале наблюдений. Изменения скорости в покрывающей толще вдоль профиля можно учесть, определяя значения скорости по прямым волнам в каждом пункте возбуждения.
Можно строить преломляющую границу для каждого интервала наблюдений раздельно, сохраняя каждый раз ее положение в базе данных. Затем их все можно вставить в финальный разрез и увязать концы.
В . Построение нескольких преломляющих границ в разрезе
Программа позволяет строить сколько угодно преломляющих границ в разрезе. Однако программа строит каждую преломляющую границу в предположении однородности покрывающей толщи по вертикали. Поэтому интерпретационная модель содержит только одну преломляющую границу. Однако это не значит, что программа не позволяет построить в разрезе более одной преломляющей границы – выделять преломляющую границу и аппроксимировать покрывающую толщу однородной средой можно на разных уровнях, и соответственно, строить любую преломляющую границу. Только делать это придется раздельно, и сохранять результаты интерпретации (положение границ и значения скоростей) раздельно. В финальном разрезе программа позволяет изобразить все проинтерпретированные границы одновременно. Более того, возможна комбинация результатов разных способов интерпретации. Например: верхний, наиболее неоднородный слой, может быть изображен как непрерывно неоднородный с изолиниями скорости, а более глубокие слои – как однородные с преломляющими границами и т.п.
Практическая часть
Э тап 1. Изображение системы наблюдений на карте-схеме
Создание проекта
Первым шагом является создание нового проекта
В дереве проекта создаются 3 уровня: “Area ”, “Line ”, “Flow ”.
Ввод параметров системы наблюдений
После входа в окно “Area
” выбираются соответствующие
29-04-2015, 00:49
