Содержание

Введение. 3

1. Теория электромагнитного поля Максвелла. 4

2. Переход от электромагнитной теории Максвелла к СТО Эйнштейна. 6

3. Специальная теория относительности А.Эйнштейна. 11

Заключение. 14

Список литературы.. 15

Введение

Для физика начала XIX в. не существовало понятия о поле как реаль­ной среде, являющейся носителем определенных сил. Но в первой половине XIX в. началось становление континуальной, полевой фи­зики. Одновременно с возникновением волновой теории света фор­мировалась совершенно новая парадигма физического исследова­ния — полевая концепция в физике. Здесь особая заслуга принадле­жит великому английскому физику М. Фарадею.

Экспериментальные открытия Фарадея были хорошо известны, и он еще при жизни приобрел огромный авторитет и славу. Однако к его теоретическим взглядам современники в лучшем случае остава­лись безразличными. Первым обратил на них серьезное внимание Дж.К.Максвелл. Он воспринял эти представления, развил их и по­строил теорию электромагнитного поля. Выработанное в оптике по­нятие «эфир» и сформулированное в теории электрических и магнит­ных явлений понятие «электромагнитное поле» сначала сближают­ся, а затем, уже в начале XX в., с созданием специальной теории относительности, полностью отождествляются.

Таким образом, понятие поля оказалось очень полезным. Будучи вначале лишь вспомогательной моделью, это понятие становится в физике XIX в. все более и более конструктивной абстракцией. Она позволяла понять многие факты, уже известные в области электри­ческих и магнитных явлений, и предсказывать новые явления. Со временем становилось все более очевидным, что этой абстракции соответствует некоторая реальность. Постепенно понятие поля за­воевало центральное место в физике и сохранилось в качестве одного из основных физических понятий.

1. Теория электромагнитного поля Максвелла

Эта теория представлена в сжатой и простой (изящной) форме в виде шести уравнений в част­ных производных. Система взглядов, которая легла в основу уравнений Максвелла, получила название теории электромагнитного поля Макс­велла.

Хотя эта система уравнений имеет простой вид, но чем больше сам Максвелл и его последователи работали над ни­ми, тем более глубокий смысл открывался им. Генрих Герц, который экспериментально получил электромагнитные из­лучения, предсказанные теорией Максвелла, говорил о неис­черпаемости уравнений Максвелла. Герц отмечал: «Нельзя изучать эту удивительную теорию, не испытывая по време­нам такого чувства, будто математические формулы живут собственной жизнью, обладают собственным разумом, - ка­жется, что эти формулы умнее нас, умнее даже самого автора, как будто они дают нам больше, чем в свое время в них было заложено».

Необходимо, однако, отметить, что свои уравнения Максвелл получал иногда вопреки правилам матема­тики. Для него исходными были физические идеи и со­ображения, которые он облекал самостоятельно в ма­тематическую форму. Поэтому для современников его теория выглядела странной и непонятной, и многими учеными воспринималась скептически до тех пор, пока Герц не дал ее всестороннее экспериментальное обос­нование. [2]

Среди постоянных величии, входящих в уравнение Макс­велла, была константа с. Применив уравнение к конкретному случаю, Максвелл нашел, что она точно совпадает со ско­ростью света. Процесс распространения поля будет продол­жаться бесконечно в виде незатухающей волны, поскольку энергия магнитного поля в пустоте полностью переходит в энергию электромагнитного поля, и наоборот. Причем свет, так же как и электромагнитное поле, распространя­ется в пространстве в виде поперечных волн со скоростью с = 300 000 км/с. Из всех этих совпадений видно, что свет име­ет электромагнитную природу, что световой поток - это по­ток электромагнитных волн. В световых волнах колебания совершают напряженности электрического и магнитного по­лей, а носителем волны служит само пространство, которое находится в состоянии напряжения.

Открытие Максвелла сравнимо по научной значимо­сти с открытием закона всемирного тяготения Ньютона. Труды Ньютона привели к введению понятия всеобще­го закона тяготения, труды Максвелла - к введению понятия электромагнитного поля и электромагнит­ной природы света. Работы Максвелла привели ученых к признанию нового типа реальности - электромагнит­ного поля, которое не совместимо с материальными точками и вещественной массой классической физики. Поле - это новая фундаментальная физическая реаль­ность. Поэтому представления о поле должны высту­пать в качестве первичных, исходных понятий. Как отме­чал А. Эйнштейн, электромагнитное поле не нуждается даже в эфире, поскольку поле само является фундамен­тальной реальностью.

В работах по принципиальным вопросам физики А. Эйн­штейн ввел понятие «программа Максвелла», которую тол­ковал как «полевую программу». Сам Эйнштейн стоял на по­зициях полевой программы и до конца своей жизни стремился построить единую теорию поля, хотя и безуспешно. [2]

В конце XIX века теория Максвелла стала играть ведущую роль в физике, и вместе с тем она вступила в противоречие с МКМ. Вместо принципа дальнодейст­вия она выдвинула и обосновала прямо противоположный принцип близкодействия, согласно которому сило­вое действие передается от точки к точке. Скорость све­та включена в новую теорию, что хотя бы в скрытой форме противоречит бесконечно большим скоростям, допускаемым в классической физике. Наконец, открыт новый тип физической реальности - поле, которое не сводится ни к материальным точкам, ни к веществу, ни к атомам. Если к этому добавить обнажившиеся про­тиворечия и слабые стороны самой классической фи­зики, то станет понятно, что в конце XIX века стре­мительно нарастал кризис механистической научной картины мира.

2. Переход от электромагнитной теории Максвелла к СТО Эйнштейна

Теорию Максвелла ряд авторов интерпретируют как но­вую - электромагнитную научную картину мира. С этим нельзя согласиться: пере­ход от одной НКМ к другой может совершиться лишь при условии, если развитие естествознания приведет к качест­венно новой трактовке не одного, а целой группы базисных понятий. Тогда как теория Максвелла в явном виде выдви­нула лишь один новый принцип - принцип близкодейст­вия. В остальном она просто вышла за рамки МКМ, посколь­ку не укладывалась в них, что само по себе не означает новой НКМ. Правда, теория Максвелла первой вышла за рамки МКМ, поэтому дальнейшая ломка МКМ была продолжени­ем дела, начатого Максвеллом.

С конца XIX - начала XX века ученые приступили к изучению качественно новых объектов в сравнении с классической физикой, и на этой основе был получен целый ряд принципиально новых результатов, позво­ливших дать новое истолкование некоторым базисным понятиям.

Первое и, по-видимому, самое мощное влияние на перестройку НКМ оказала теория относительности выдающегося физика-теоретика XX столетия Альбер­та Эйнштейна (1879-1955).

Поскольку в теории относительности Эйнштейна большую роль играет принцип относительности движения в формули­ровке Ньютона, то полезно еще раз привести ее. Впервые этот принцип ввел Галилей, о чем говорилось выше. С уче­том идей Декарта Ньютон уточнил и расширил формулиров­ку Галилея. В частности, в качестве систем отсчета он брал не тела, а декартову систему координат. [2]

Среди систем отсчета выделяют инерциальные, особенность которых состоит в том, что для них выполняется прин­цип относительности движения.

Принцип относительности движения означает, что во всех инерциальных системах отсчета механические процессы ин­вариантны. Иначе говоря, два наблюдателя в одной и другой инерциальной системе отсчета увидят, что в их системах фи­зические процессы протекают одинаково. Это означает также, что переход от одной инерциальной системы отсчета к другой осуществляется по правилам галилеевых преобразований, рассмотренных выше. И наоборот, если при переходе от одной системы отсчета к другой правила галилеевых пре­образований не выполняются, то и принцип относительности движения не выполняется, поэтому такие системы отсчета не будут инерциальными. Таким смыслом наполнен принцип относительности движения в классической механике.

Эйнштейн был тонким мыслителем, он всегда стремился максимально упорядочить логическую структуру физических теорий. Физики-теоретики того вре­мени, включая Эйнштейна, стремились теоретически и ло­гически упорядочить электродинамику Максвелла. В итоге таких усилий возникли новые теории специальная и общая теория относительности Эйнштейна.

Теории электромагнитного поля Максвелла были присущи два недостатка:

1. Она не совмещалась с принципом относительно­сти движения классической физики, поскольку ее урав­нения оказались неинвариантными относительно пре­образований Галилея. Это был существенный изъян, поскольку вся практика подтверждала и подтверждает этот принцип, и никакая теория не опровергает его.

2. Полевая картина физической реальности Макс­велла оказалась теоретически неполной и логически противоречивой, так как трактовка электрического по­ля и электрически заряженных частиц (носителей поля) не была увязана концептуально. Эйнштейн отмечал: тео­рия Максвелла хотя и правильно описывает поведение электрически заряженных частиц, но не дает теории этих частиц. Следовательно, они должны рассматриваться на основе классической механики как материальные точ­ки, расположенные в пространстве дискретно, что про­тиворечит понятию поля. Последовательная полевая теория требует непрерывности всех элементов теории. [2]

Решение этого вопроса, данное Эйнштейном, оригинально и поучительно. Объектом изучения в классической механике были или материальные точки, или точки пространства, или моменты времени. Он отвергает все эти разделительные «или».

Объектом теории относительности выступают «физические со­бытия» как целостные объекты, в которых объединены по­нятия материи, движения, пространства, времени. Физической реальностью, отмечал Эйнштейн, обладают не точки прост­ранства и не моменты времени, а только сами события, опре­деленные четырьмя числами х, у, z, t. «Законы природы при­мут наиболее удовлетворительный с точки зрения логики вид, будучи выражены как законы в четырехмерном пространст­венно-временном континууме» [4].

Остановимся теперь на рассмотрении первого не­достатка. Анализ показал, что уравнения Максвелла неинвариантны относительно галилеевых преобразо­ваний. Это значит, что при переходе от одной инерциальной системы отсчета к другой форма уравнений оказывалась разной. Это равносильно тому, что в раз­ных системах отсчета один и тот же физический процесс осуществлялся по разным законам, что противоречит науке. Как же уберечь теорию Максвелла от этого не­достатка?

В 1890 году Г. Герц искусственно подобрал систему урав­нений, инвариантных относительно галилеевых преобразо­ваний, которые в частном случае покоящегося тела обраща­ются в уравнения Максвелла. Однако уравнения Герца про­тиворечили опытно установленному постоянству скорости света (300 000 км/с).

Еще один вариант переработки уравнений Максвола предпринял голландский физик-теоретик Г.Лоренц, но и его уравнения оказались неинвариантными относительно галилеевых преобразований.

И тогда поступили, как в той известной притче: «Ес­ли гора не идет к Магомеду, то Магомед идет к горе» Поскольку не удалось переформулировать уравнения Максвелла так, чтобы они стали инвариантными относительно галилеевых преобразований, то Лоренц предпринял обратный ход: решил сами правила галилеевых преобразо­ваний видоизменить (проще говоря, подогнать) так, чтобы относительно этих правил уравнения Максвелла оказались инвариантными.

Лоренцевы преобразования - это новые (отличные от га­лилеевых) правила перехода от одной инерциалыюй системы отсчета к другой. Для одной точки в декартовой системе координат без штрихов при переходе к системе отсчета со штрихами лоренцевы преобразования устанавливают сле­дующие правила:

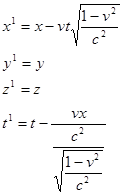
Как видим, отличие правил лоренцевых преобразований от галилеевых существенно. Это отличие станет еще более зримым, если определять не координату материальной точки, а размер макроскопического тела, например, жесткого стерж­ня длиной l. Такой стержень имеет начальную и конечную точки на оси х¹ , х. Определив координаты этих точек и вычитая из координаты с большим значением координату с меньшим значением, получим математическое выражение для длины (l ) и для времени (t ) движущегося стержня:

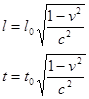
Здесь l -длина движущегося стержня, l ₀ - длина покоящеюся стержня, v - скорость движения стержня (системы отсчета), t - время покоящегося стержня, t₀ - время движущегося стерж­ня, с - скорость света в пустоте. [2]

Рассмотрим соотношения l и t сначала формально. При малых значениях величины v, по сравнению со скоростью света, значением дроби и подкоренного выражения можно пре­небречь. Тогда l = l ₀ и t = t ₀ , что равносильно возврату от лоренцевых преобразований к галилеевым. Если же значения величины v достаточно большие (сравнимые со скоростью света), то значением подкоренного выражения нельзя пре­небречь и оно будет уменьшаться. Соответственно этому значение величины l будет уменьшаться, а значение величи­ны t - возрастать. В таком случае с ростом скорости движе­ния (v) различия между преобразованиями Лоренца и пре­образованиями Галилея будут нарастать.

Итак, Лоренц искусственно получил новые правила перехода от одной инсрпиалыюй системы к другой. При этом уравнения Максвелла оказываются инвариант­ными в любых инерциальных системах отсчета. Одна­ко неизвестной остается реальность самих преобразо­ваний Лоренца: имеют они физический смысл или пег? Поскольку эти правила получены искусственно, то сам Лоренц отказывался придавать им физический смысл. Над ним довлели представления классической физики о неизменности пространства и времени. [3]

Иначе подошел к этому вопросу А. Эйнштейн. За фактом хорошей согласованности лоренцевых преобразований с теорией Максвелла он угадал реальный физический смысл самих преобразо­ваний. Для этого он предпринял попытку дедук­тивного построения теории, которая бы наполнила преобразования Лоренца физическим смыслом. Иначе говоря, он задался целью углубить пони­мание принципа относительности путем его раз­вертывания в теорию относительности.

3. Специальная теория относительности А.Эйнштейна

В качестве постулатов дедуктивной теории он принял два принципа. Прежде всего - принцип относительности клас­сической физики, резко расширив его, распространив его не только на механическое движение, но и на электромагнитные и световые процессы. Уже в исходной посылке Эйнштейн объединил классическую механику и электромагнитную тео­рию Максвелла. В качестве второго постулата он взял прин­цип постоянства скорости света в пустоте. Поскольку скорость света в качестве константы включена в уравнения Максвел­ла, то Эйнштейн принял эту константу и для классической физики. Тем более что в конце XIX века экспериментально было надежно установлено, что скорость света конечна, хотя и велика. Позже было принято считать, что скорость снега в пустоте составляет примерно 300 000 км/с.

Таким образом, постулатами частной теории отно­сительности являются два принципа.

1. Принцип относительности движения, которому Эйнштейн придал всеобщий характер, распространив его с механических на магнитные, электрические и све­товые процессы.

2. Принцип постоянства скорости света в пустоте, со­ставляющей 300 000 км/с. Эта скорость является макси­мальной возможной скоростью распространения ма­териальных взаимодействий.

Из этих двух физических принципов Эйнштейн заново вывел математические правила преоб­разования Лоренца. Но теперь математическая форма соотношений l и t наполнена физичес­ким смыслом, поскольку их Эйнштейн вывел из физических посылок. Из соотношений l и t можно видеть, что, когда скорость движения те­ла становится сравнимой со скоростью света, ли­нейный размер тела физически сокращается в на­правлении его движения. Со временем происходят противоположные изменения: его течение замед­ляется, ритмика течения времени растягивается. [1]

Если скорость движения тела приближается к скорости света, то тело сжимается в направлении движения до такой степени, что превращается в плоскую фигуру (в лепешку). Значит, допускавшиеся в классической физике скорости, пре­вышающие скорость света в пустоте, не имеют физического смысла. Отсюда следует, что скорость распространения ма­териальных взаимодействий в природе не может превышать скорость света в пустоте.

Таким образом, дедуктивные следствия из физичес­ких постулатов привели Эйнштейна к построению раз­вернутой содержательной теории, которую затем он на­зовет частной, или специальной. Специальная теория относительности (СТО) обобщает классическую физи­ку и электродинамику Максвелла и выступает как реля­тивистская физика, в которой дается новая теория таких понятий, как масса, движение, пространство, время.

В классической физике пространство оторвано от времени, и они рассматриваются как абсолютные. Абсолютны они потому, что оторваны от движущихся материальных тел. Специальная теория относительности устанавливает зависи­мость пространства и времени от скорости движения мате­риальных тел. Кроме того, она устанавливает неразрывную связь пространства и времени, поскольку они изменяются синхронно, и притом в противоположных направлениях: при больших скоростях движения тел их линейный размер сокра­щается в направлении движения, а ритмика течения времени растягивается. Поэтому рассмотрение физических событий должно относиться к единому четырехмерному пространст­венно-временному континууму: х, у, z, t.

Свою критику классической механики Эйнштейн на­чал с пересмотра «абсолютного времени», понимаемого как одновременность всех событий в мире. В класси­ческой физике одновременности двух событий в точках пространства А и В обосновывалась переносом часов из одной точки в другую. Несостоятельность этого аргу­мента вытекает из факта конечной скорости распрост­ранения материальных взаимодействий. [3]

Хотя СТО базируется на рассмотрении инерциальных систем отсчета, она все же позволяет установить важную зависимость для ускоренного движения. В ре­лятивистской физике считается, что чем выше ско­рость движения тела, тем труднее увеличить ее. Пос­кольку сопротивление изменению скорости тела на­зывается его массой (инерционной), то отсюда следует, что масса тела возрастает с ростом скорости его дви­жения. В классической механике массу рассматрива­ют как постоянную величину - это релятивистская мас­са покоя. В СТО массу считают переменной величиной, зависящей от скорости движения:

Это изменение массы можно обнаружить лишь при больших скоростях, например, при движении электро­нов вокруг ядра атома, что и было затем установлено экспериментально.

После опубликования СТО Эйнштейн из зависимости массы от скорости движения математическим путем получил новое следствие - вывод о равенстве инертной и весовой массы.

Отсюда ученый сделал два радикальных вывода:

а) о равенстве весовой и инертной массы,

б) об эквивалентности массы и энергии.

Случай с кинетической энергией Эйнштейн обобщил на все формы энергии: энергия в любой форме ведет себя как масса. Энергия является массой, а масса представляет собой энергию. Энергия и масса преобразуются друг в друга по формуле:

E = m


29-04-2015, 02:11