Продольный эффект Фарадея

Продольный магнитооптический эффект Фарадея.

1. Основные свойства эффекта.

Продольный магнитооптический эффект состоит в повороте плоскости поляризации луча света, проходящего через прозрачную среду, находящуюся в магнитном поле. Этот эффект был открыт в 1846 году. Открытие магнитооптического эффекта долгое время имело значение в чисто физическом аспекте, но за последние десятилетия оно дало много практических выходов. Также были открыты другие магнитооптические эффекты, в частности, хорошо известный эффект Зеемана и эффект Керра, проявляющийся в повороте плоскости поляризации луча, отраженного от намагниченной среды. наш интерес к эффектам Фарадея и Керра обусловлен их применением в физике, оптике и электронике. К ним относятся :

- определение эффективной массы носителей заряда или их плотности в полупроводниках;

- амплитудная модуляция лазерного излучения для оптических линий связи и определение времени жизни неравновесных носителей заряда в полупроводниках;

- изготовление оптических невзаимных элементов;

- визуализация доменов в ферромагнитных пленках;

- магнитооптическая запись и воспроизведение информации как в специальных, так и бытовых целях.

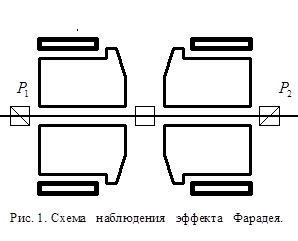
Принципиальная схема устройства для наблюдения и многих применений эффекта Фарадея показана на рис. 1. Схема состоит из источника света, поляризатора, анализатора и фотоприемника. Между поляризатором и анализатором помещается исследуемый образец. Угол поворота плоскости поляризации отсчитывается по углу поворота анализатора до восстановления полного гашения света при включенном магнитном поле.

Интенсивность прошедшего пучка определяется законом Малюса

На этом основана возможность использования эффекта Фарадея для модуляции пучков света. Основной закон, вытекающий из измерений угла поворота плоскости поляризации , выражается формулой

где - напряженность магнитного поля, - длина образца, полностью находящегося в поле и - постоянная Верде, которая содержит в себе информацию о свойствах, присущих исследуемому образцу, и может быть выражена через микроскопические параметры среды.

Основная особенность магнитооптического эффекта Фарадея состоит в его невзаимности, т.е. нарушении принципа обратимости светового пучка. Опыт показывает, что изменение направления светового пучка на обратное /на пути "назад"/ дает такой же угол поворота и в ту же сторону, как на пути "вперед". Поэтому при многократном прохождении пучка между поляризатором и анализатором эффект накапливается. Изменение направления магнитного поля, напротив, изменяет направление вращения на обратное. Эти свойства объединяются в понятии "гиротропная среда".

2. Объяснение эффекта циркулярным магнитным двупреломлением.

Согласно Френелю, поворот плоскости поляризации является следствием циркулярного двупреломления. Циркулярная поляризация выражается функциями для правого вращения /по часовой стрелке/ и для вращения против часовой стрелки. Линейная поляризация может рассматриваться как результат суперпозиции волн с циркулярной поляризацией с противоположным направлением вращения. Пусть показатели преломления для правой и левой циркулярной поляризации неодинаковы. Введем средний показатель преломления и отклонение от него . Тогда получим колебание с комплексной амплитудой

что соответствует вектору , направленному под углом к оси X. Этот угол и есть угол поворота плоскости поляризации при циркулярном двупреломлении, равный

3. Вычисление разности показателей преломления.

Из теории электричества известно, что система зарядов в магнитном поле вращается с угловой скоростью

которая называется скоростью прецессии Лармора.

Представим себе что мы смотрим навстречу циркулярно поляризованному лучу, идущему через среду, вращающуюся с частотой

Лармора; если направления вращения вектора в луче и Ларморовского вращения совпадают, то для среды существенна относительная угловая скорость , а если эти вращения имеют разные направления, то относительная угловая скорость равна .

Но среда обладает дисперсией и мы видим, что

Отсюда получаем формулу для угла поворота плоскости поляризации

и для постоянной Верде

4. Практические применения эффекта Фарадея.

Эффект Фарадея приобрел большое значение для физики полупроводников при измерениях эффективной массы носителей заряда. Эффект Фарадея очень полезен при исследованиях степени однородности полупроводниковых пластин, имеющих целью отбраковку дефектных пластин. Для этого проводится сканирование по пластине узким лучом-зондом от инфракрасного лазера. Те места пластины, в которых показатель преломления, а следовательно, и плотность носителей заряда, отклоняются от заданных, будут выявляться по сигналам фотоприемника, регистрирующего мощность прошедшего через пластину излучения.

Рассмотрим теперьамплитудные и фазовые невзаимные элементы /АНЭ и ФНЭ/ на основе эффекта Фарадея. В простейшем случае оптика АНЭ состоит из пластинки специального магнитооптического стекла, содержащего редкоземельные элементы, и двух пленочных поляризаторов /поляроидов/. Плоскости пропускания поляризаторов ориентированы под углом друг к другу. Магнитное поле создается постоянным магнитом и подбирается так, чтобы поворот плоскости поляризации стеклом составлял . Тогда на пути "вперед" вся система будет прозрачной, а на пути "назад" непрозрачной, т.е. она приобретает свойства оптического вентиля. ФНЭ предназначен для создания регулируемой разности фаз двух линейно поляризованных встречных волн. ФНЭ нашел применение в оптической гирометрии. Он состоит из пластинки магнитооптического стекла и двух пластинок , вносящих разность фаз и . Магнитное поле, как и в АНЭ создается постоянным магнитом. На пути "вперед" линейно поляризованная волна, прошедшая пластинку преобразуется в циркулярно поляризованную с правым вращением, затем проходит магнитооптическую пластинку с соответствующей скоростью и далее через вторую пластинку , после чего линейная поляризация восстанавливается. На пути "назад" получается левая поляризация и эта волна проходит магнитооптическую пластинку со скоростью, отличающейся от скорости правой волны, и далее преобразуется в линейно поляризованную. Введя ФНЭ в кольцевой лазер, мы обеспечиваем разность времен обхода контура встречными волнами и вытекающую отсюда разность их длин волн.

В непосредственной близости к собственной частоте осцилля-

торов эффект Фарадея описывается более сложными закономерностями. В уравнении движения осциллирующего электрона не-

обходимо учитывать затухание

Необходимо отметить, что для циркулярно поляризованных волн, распространяющихся вдоль магнитного поля, дисперсионная кривая и спектральный контур линии поглощения имеют для данной среды тот же вид, что и при отсутствии магнитного поля, отличаясь только сдвигом по шкале частот на вправо для волны с положительным направлением вращения вектора и на влево - для волны с противоположным направлением вращения .

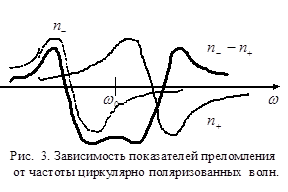
На рисунке 3штриховыми линиями показаны графики функций и , а их разность - сплошной линией. Видно, чтовокрестности дважды изменяется знак эффекта Фарадея: в интервале частот вблизи поворот направления поляризации происходит в отрицательную сторону, а вне этого интервала - вположительную. Однако следует иметь в виду, что в данном случае эффект не сводится только к повороту направления поляризации падающей волны. В окрестности существенно поглощение света, причем при данном значении коэффициенты затухания для циркулярно поляризованных составляющих падающей волны имеют разные значения (круговой дихроизм). Поэтому после прохождения через образец амплитуды этих составляющих не равны и при их сложении получается эллиптически поляризованный свет.

Важно сознавать, что в эффекте Фарадея магнитное поле влияет на состояние поляризации света лишь косвенно, изменяя характеристики среды, в которой распространяется свет. В вакууме магнитное поле никакого влияния на свет не оказывает.

Обычно угол поворота направления поляризации очень мал, но благодаря высокой чувствительности экспериментальных методов измерения состояния поляризации эффект Фарадея лежит в основе совершенных оптических методов определения атомных констант.