Релятивистская теория возникновения инерции

, (6.4)

Как следует из (6.4), всякое структурное изменение положения частиц, приводит к изменению потенциальной энергии и как следствие, к дефекту массы. Не с этим ли связано многообразие элементарных частиц? Обнаруживая одну и ту же частицу в разных энергетических состояниях принимаем ее за разные? Для электромагнитных взаимодействий дефект составляет величину порядка = , где - постоянная тонкой структуры, что очень мал, но для сильных взаимодействий он может стать значительным.

Определим полную энергию релятивистской частицы. Полагая находим

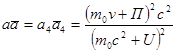, , (6.5)

(6.6)

- энергия покоя частицы в потенциальном поле . Она определяет энергию связи и показывает, что дефект массы вызван изменением потенциальной энергии частицы.

Эти формулы обобщают соответствующие формулы СТО и в обширных комментариях не нуждаются.

7. Квантовая инерцодинамика – основа единой теории поля

При выводе уравнений инерцодинамики мы никаких ограничений на выбор зарядов и их полей не делали. Поэтому уравнения инерцодинамики включают в себя все известные поля и их можно рассматривать как систему уравнений единого поля. Проблема состоит в их квантовании. На первый взгляд, тут никаких проблем нет. Из определения полного импульса следует уравнение Клейна – Гордона -

Фока

(7.1)

Оно общековариантно и поскольку уравнения инерцодинамики образованы из этого импульса и его производных, то достаточно заменить импульс оператором и воздействовать волновой функцией и уравнения будут квантованным. Однако это не так. Уравнение (7.1) квадратично, а уравнение движения должно быть первого порядка поскольку при возведении всякой функции в квадрат часть информации теряется. В данном случае теряется информация, касающаяся внутренних степеней свободы частицы, такие как спин, поляризация, четность, странность и др.

Чтобы избежать этих потерь, умножая на операторы , образуем функционал первого порядка

, (7.2)

Определим таким образом, чтобы из (7.2) в пределе получилось (7.1). Для этого необходимо потребовать, чтобы были антикоммутирующими

(7.3)

Явный вид этих операторов, напоминающих операторы Дирака, нам пока не потребуется, так как природа частицы не конкретизируется. Воздействуя на (7.2) сопряженным функционалом, имеем

, (7.4)

где ,

, (7.5)

Уравнение (7.4) отличается от (7.1) последним членом. Он обращается в нуль, если вещественны. Вводя оператор ковариантного дифференцирования

, (7.6)

образуем «тензор напряженности инерционного поля»

, (7.7)

с компонентами , ,

, , (7.8)

, ,

Диференцируя по , представим систему уравнений инерцодинамики (7.9) – (7.11)

(7.9)

, ,

, (7.10)

где , , (7.11)

,

в четырехмерной форме

, (7.12)

,

,

(Запятая перед индексами означает ковариантное дифференцирование). Воздействием на волновую функцию (7.2) преобразуется в систему нелинейных квантомеханических уравнений поля. Если в сохранить только , а в только , то она трансформируется в обыкновенные дифференциальные уравнения в частных производных с потенциалом типа потенциала поля Янга-Миллса

(7.13)

Переход от лагранжиана к гамильтониану осуществляется по стандартной схеме

(7.14)

где

Во всех этих уравнениях определяющим является - импульс. Он зависит от многих факторов и в общей форме не определяется. Его можно задавать только для конкретной модели. Один из возможных вариантов состоит в разложении по группам симметрии Ли /9/. Генераторы групп составляются из величин, характеризующих заряд данного мультиплета, а параметры – из полей, связывающие эти заряды. Генератор ой группы содержит матриц го порядка , а параметры , так же как и волновая функция , образуют - компонентную матрицу-столбец из частиц, носителей взаимодействия. Число компонент жестко связано с рангом матрицы и равно . Гамильтониан взаимодействия соответствующий ой группы, равен

(7.15)

Суммирование проводится по компонентам всех сортов частиц и их полей.

В качестве примера рассмотрим электромагнитное и электрослабое взаимодействия. В микромире грави-инерционные поля пренебрежимо малы и ими можно пренебречь, поэтому суммирование по опустим и отождествим с электрическим зарядом .

Электромагнитное взаимодействие. Это наиболее простой тип взаимодействия, которому соответствует унарная группа . При , имеем

,, . (7.16)

где- векторный потенциал.

Электрослабое взаимодействие. Оно описывается группой, т.е. квадратной матрицей с рангом 2. При число компонент равно .Генераторы этой группы образуют пространственный вектор, компоненты которого состоят из квадратной матрицы. В качестве таких матриц обычно, принимают матрицы Паули , а в качестве параметров – массивные бозоны Вейнберга-Салама . В этом случае

(7.17)

следовательно, , (7.18)

где единичная матрица второго порядка.

Аналогично строятся и группы более высокого ранга. Скажем, группа , описывающая взаимодействие кварков, содержит матриц третьего порядка. В качестве таких матриц можно использовать матрицы Гелл-Манна , с базисами, образованными из глюонов, связывающие кварки. Методы расчета этих полей хорошо известны и их рассматривать не будем.

Таким образом, соответствующим представлением-импульса все известные типы взаимодействия объединяются, образуя единое динамическое поле. Оно формируется всеми видами материи и играет важную роль в системе мироздания.

Список литературы

1. Ландау Л.Д и Лифшиц Е.М. Теория поля. М., 1973.

2. Эйнштейн А. Собрание научных трудов. М. т. 4, 1965

3. Фок В.А. Теория пространства, времени и тяготения. М., 1961

4. Владимиров Ю.С. Система отсчета в теории гравитации. М. Энергоиздат.1982

5. Sadykov B.S. Gravitation & Cosmology. RGS,Vol. 7 (2001), No 3 (27), Moscow

6. Садыков Б.С. Физика и механика на пороге ХХ1 века. Сб. No 1-3, М. 2000.

7. Садыков Б.С. Известия вузов. Физика. № 6, 1981.

8. Климишин И.А. Релятивистская астрономия. «Наука», М. 1998

9. Салбери А. Квантовая механика и физика элементарных частиц. “Мир.”, М. 1989