Классификация различных способов структурного резервирования осуществляется по следующим признакам:
1) по схеме включения резерва:
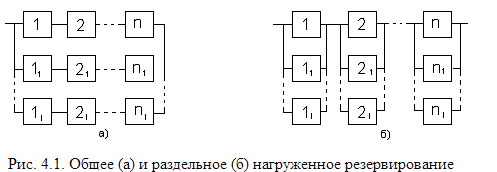
-общее резервирование, при котором резервируется объект в целом;
-раздельное резервирование, при котором резервируются отдельные элементы или их группы;
- смешанное резервирование, при котором различные виды резервирования сочетаются в одном объекте;
2) по способу включения резерва:
- постоянное резервирование, без перестройки структуры объекта при возникновении отказа его элемента;
- динамическое резервирование, при котором при отказе элемента происходит перестройка структуры схемы. В свою очередь подразделяется на:
а) резервирование замещением, при котором функции основного элемента передаются резервному только после отказа основного;
б) скользящее резервирование, при котором несколько основных элементов резервируется одним или несколькими резервными, каждый из которых может заменить любой основной (т.е. группы основных и резервных элементов идентичны).
3) по состоянию резерва:
- нагруженное резервирование, при котором резервные элементы (или один из них) находятся в режиме основного элемента;
- облегченное резервирование, при котором резервные элементы (по крайней мере один из них) находятся в менее нагруженном режиме по сравнению с основными;
-ненагруженное резервирование, при котором резервные элементы до начала выполнения ими функций находятся в ненагруженном режиме.
Основной характеристикой структурного резервирования является кратность резервирования - отношение числа резервных элементов к числу резервируемых ими основных элементов, выраженное несокращаемой дробью (типа 2:3; 4:2 и т.д.). Резервирование одного основного элемента одним резервным (т.е. с кратностью 1:1) называется дублированием .
Количественно повышение надежности системы в результате резервирования или применения высоконадежных элементов можно оценить по коэффициенту выигрыша надежности , определяемому как отношение показателя надежности до и после преобразования системы. Например, для системы из n последовательно соединенных элементов после резервирования одного из элементов (k-го) аналогичным по надежности элементом коэффициент выигрыша надежности по вероятности безотказной работы составит
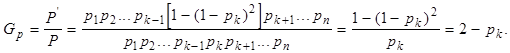(4.1)
Из формулы (4.1) следует, что эффективность резервирования (или другого приема повышения надежности) тем больше, чем меньше надежность резервируемого элемента (при 
, при 
). Следова-тельно, при структурном резервировании максимального эффекта можно до-биться при резервировании самых ненадежных элементов ( или групп элемен-тов).
В общем случае при выборе элемента (или группы элементов) для повышения надежности или резервирования необходимо исходить из условия обеспечения при этом максимального эффекта. Например, для мостиковойсхемы (рис. 3.2,а) из формулы (3.21) можно получить выражение для частных производных вероятности безотказной работы системы по вероятности безотказной работы каждого из элементов, которые для идентичных по надежности элементов принимают следующий вид:
(4.2)
(4.3)
Очевидно, максимальное увеличение надежности системы обеспечит увеличение надежности или резервирование того элемента, частная производная для которого при данных условиях принимает максимально положительное значение. Сравнение выражений (4.2) и (4.3) показывает, что при любых положительных значениях p и q выражение (4.2) больше выражения (4.3) и, следовательно, в мостиковой схеме с идентичными элементами эффективность повышения надежности или резервирования “периферийных” элементов 1, 2, 4 и 5 (см. рис. 3.2, а) выше, чем диагонального элемента 3, если в качестве критерия эффективности взять вероятность безотказной работы.
Таким образом, наибольшее влияние на надежность системы оказывают элементы, обладающие высоким значением производной 
, а при последова-тельном соединении - наименее надежные.
В более сложных случаях для выбора элементов, подлежащих изменению, используются как аналитические, так и численные методы оптимизации надежности.
4.2. Расчет надежности систем с резервированием
Расчет количественных характеристик надежности систем с резервированием отдельных элементов или групп элементов во многом определяется видом резервирования. Ниже рассматриваются схемы расчетов для самых распространенных случаев простого резервирования, к которым путем преобразований может быть приведена и структура смешенного резервирования. При этом расчетные зависимости получены без учета надежности переключающих устройств, обеспечивающих перераспределение нагрузки между основными и резервными элементами (т.е. для “идеальных” переключателей). В реальных условиях введение переключателей в структурную схему необходимо учитывать и в расчете надежности систем.
Расчет систем с нагруженным резервированием осуществляется по формулам последовательного и параллельного соединения элементов аналогично расчету комбинированных систем (п. 3.5). При этом считается, что резервные элементы работают в режиме основных как до, так и после их отказа, поэтому надежность резервных элементов не зависит от момента их перехода из резервного состояния в основное и равна надежности основных элементов.
Для системы с последовательным соединением n элементов (рис. 2.1) при общем резервировании с кратностью l (рис. 4.1, а)
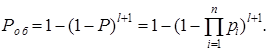(4.4)
В частности , при дублировании (l =1)
(4.5)
При раздельном резервировании (рис. 4.1,б)
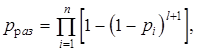(4.6)
а при раздельном дублировании (l =1)
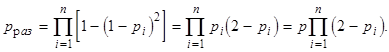(4.7)
Тогда коэффициенты выигрыша надежности по вероятности безотказной работы при дублировании
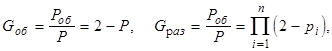(4.8)
откуда следует, что раздельное резервирование эффективнее общего (например, для системы из трех одинаковых элементов при 
, 
.
При ненагруженном резервировании резервные элементы последовательно включаются в работу при отказе основного, затем первого резервного и т.д. (рис. 4.2), поэтому надежность резервных элементов зависит от момента их перехода в основное состояние. Такое резервирование в различных ТС встречается наиболее часто, т.к. оно по сути аналогично замене отказавших элементов и узлов на запасные.
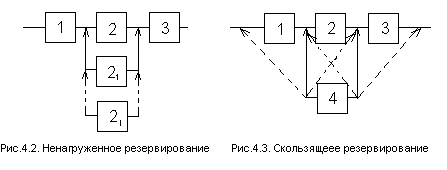
Если резервные элементы до их включения абсолютно надежны, то для системы с ненагруженным резервированием кратности l (всего элементов l+1 )
(4.9)
т.е. вероятность отказа в (l+1 )! раз меньше, чем при нагруженном (параллельном соединении, см. формулу (3.7)).
Для идентичных по надежности основного и резервного элементов
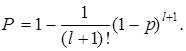(4.10)
При экспоненциальном распределении наработки (простейшем потоке отказов, см. 1.7) в случае 
можно воспользоваться приближенной формулой
(4.11)
При ненагруженном резервировании средняя наработка на отказ
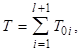(4.12)
а для идентичных элементов 
Облегченное резервирование используется при большой инерционности переходных процессов, происходящих в элементе при его переходе из резервного в основной режим, и нецелесообразности применения нагруженного резервирования из - за недостаточного выигрыша в надежности (в РЭС это характерно для устройств на электровакуумных приборах). Очевидно, облегченный резерв занимает промежуточное положение между нагруженным и ненагруженным.
Точные выражения для расчета надежности систем при облегченном резервировании весьма громоздки и неоднозначны, однако при экспонен-циальном распределении наработки справедлива приближенная формула
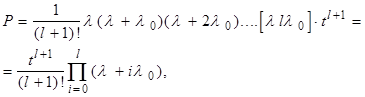(4.13)
где 
- интенсивность отказов элементов в облегченном режиме, l
- кратность резервирования.
Скользящее резервирование используется для резервирования нескольких одинаковых элементов системы одним или несколькими одинаковыми резервными (рис. 4.3, здесь все элементы идентичны, а элемент 4 - избыточный). Очевидно, отказ системы произойдет, если из общего количества идентичных элементов (основных и резервных) число отказавших превышает число резервных. Расчет вероятности безотказной работы систем со скользящим резервированием аналогичен расчету систем типа “m из n”, см. п. 3.3.
5. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Задание на курсовую работу (КР) содержит в качестве исходных данных структурную схему надежности технической системы (ТС) и интенсивность отказов ее элементов (см. п. 7). То есть студент оказывается в ситуации, когда выполнены п. 1 - 6 анализа структурной надежности ТС (см. разд. 2), и ему надлежит в первую очередь выполнить п. 7 - составить расчетные зависимости для определения показателей надежности системы для различных значений наработки t , чтобы графически изобразить вероятность безотказной работы P(t) как функцию наработки.
Поскольку заданная схема надежности является комбинированной, ее следует подвергнуть декомпозиции, как это описано в п. 3.5. Далее, вводя соответствующие квазиэлементы, преобразовать исходную схему к простейшему виду и , используя соответствующие формулы п. 3.1 - 3.4, для ряда значений наработки t в предположении простейшего потока отказов формулы (1.7)вычислить значениявероятностей безотказной работы элементов, квазиэлементов и всей системы.В пояснительной записке следует привести все промежуточные преобразования исходной схемы, конкретные рабочие расчетные формулы с их обоснованием, а результаты расчета представить в виде таблицы, в которой по столбцам изменяется значение наработки t , а по строкам в столбцах приводятся вычисленные значения вероятностей безотказной работы элементов,квазиэлементов и всей системы, полученные по рабочим формулам. При этом диапазон измерения наработки t должен обеспечить снижение вероятности безотказной работы системы до уровня 0.1 - 0.2 и содержать не менее 8-10 значений аргумента.
После этого строится график зависимости P(t)
по результатам расчета. И него графически по заданному значению
определяется
- процентная наработка системы (см. (1.9)), 
.
По заданию требуется предложить способы увеличения - процентной наработки в 1.5 раза за счет повышения надежности элементов и за счет структурного резервирования.
Предварительно следует определить элемент или квазиэлемент окончательно преобразованной схемы, повышение надежности которого даст максимальный эффект в отношении надежности всей системы.Критерии выбора приведены в п. 4.1. Поскольку аналитически определить производные вида (4.2), (4.3) обычно не удается, выбор элемента может быть осуществлен по величине вероятности безотказной работы.
Для дальнейших действий необходимо вычислить требуемое улучшенное значение- процентной наработки 
элементарным умножением на 1.5. Следовательно, чтобы удовлетворить заданию в отношении повышения надежности системы,необходимо обеспечить вероятность безотказной работы 
за время 
. Теперь следует повторить расчет надежности элементов, квазиэлементов и всей системы за время и дополнить этим столбцом предыдущую таблицу . Зная вероятности безотказной работы всех элементов преобразованной схемы и требуемое значение 
, легко определить,какую вероятность безотказной работы
за время
должен иметь квазиэлемент, избранный для модернизации.
По первому варианту модернизации необходимо определить интенсивности отказов элементов, входящих в данный квазиэлемент, при которых при неизменной структуре квазиэлемента обеспечивалось бы необходимое значение 
. Проще это осуществить графоаналитическим методом, задавая ряд пропорционально уменьшенных (по сравнению с исходной) интенсивностей отказов для составляющих квазиэлемента и просчитывая каждый раз величину . Из построенного по этим данным графика можно определить необходимую кратность снижения интенсивности отказов элементов и сами значения интенсивности. Для найденного решения следует выполнить проверочный расчет вероятности безотказной работы системы за время .
По второму методу надежность выбранного квазиэлемента можно повысить за счет резервирования без изменения надежности составляющих элементов. При этом, основываясь на рекомендациях и соображениях, изложенных в п. 4.1, 4.2, учитывая структуру модернизируемого квазиэлемента, нужно выбрать, какие его составляющие элементы и как следует резервировать для достижения наибольшего эффекта. Далее остается определить необходимую кратность резервирования
. Поскольку есть величина дискретная, аналитически ее определить невозможно. Для решения задачи нужно последовательно увеличивать кратность резервирования, начиная с единицы, каждый раз по соответствующим формулам из п. 4.2 определять величину вероятности безотказной работы квазиэлемента в течении времени. Как только необходимое значение будет обеспечено, окажется реализованным второй метод повышения надежности системы.Для найденного решения также необходимо провести проверку вероятности безотказной работы системы за время. Модернизированную структуру с резервированием следует привести в пояснительной записке.
Для построения зависимостей вероятностей безотказной работы от времени для модернизированной системы по первому и второму методу удобно дополнить ранее составленную таблицу соответствующими строками. Графики этих зависимостей следует изобразить совместно с кривой P(t ) исходной системы.
Полученное семейство кривых позволяет провести сравнение двух вариантов модернизации, которое следует привести в качестве вывода к работе.
Пояснительная записка должна быть оформлена в соответствии с СТП КрПИ 3.1- 92 “Текстовые документы. Требования к оформлению”. Все действия и использование расчетных сотношений должны быть объяснены и обоснованы.Для заимствуемой информации (формулы, численные значения констант) необходимо указать источник заимствования.
Задания на курсовую работу приведены в разд. 6, а в разд. 7 - пример расчета надежности.
6. ИСХОДНЫЕ ДАННЫЕ К РАБОТЕ
По структурной схеме надежности технической системы в соответствии с вариантом задания, требуемому значению вероятности безотказной работы системы и значениям интенсивностей отказов ее элементов 
(табл. 6.1) требуется:
1. Построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0.1 - 0.2.
2. Определить - процентную наработку технической системы.
3. Обеспечить увеличение - процентной наработки не менее, чем в 1.5 раза за счет:
а) повышения надежности элементов;
б) структурного резервирования элементов системы.
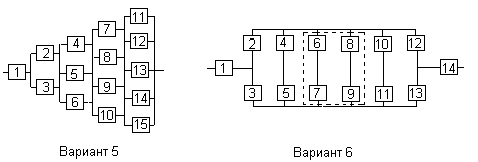
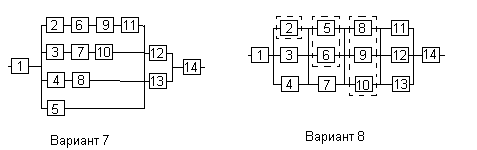
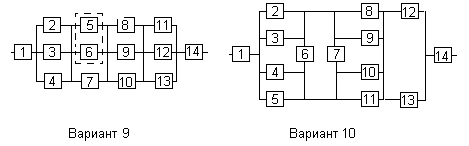
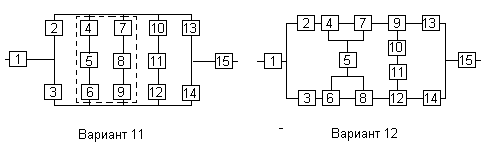
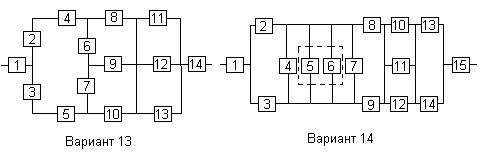
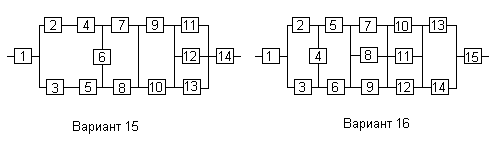
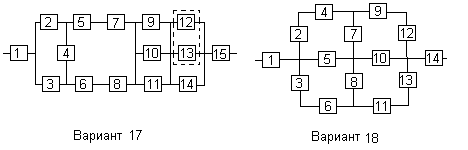
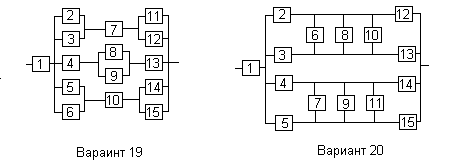
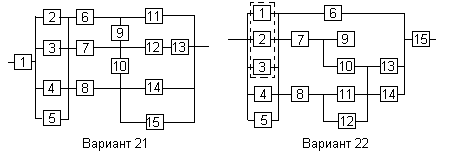
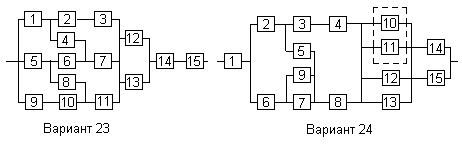
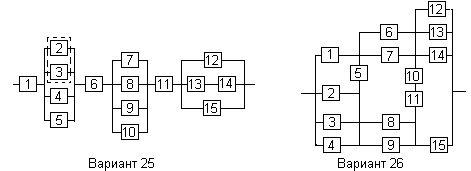
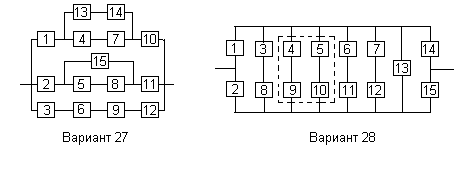
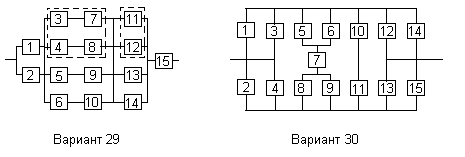
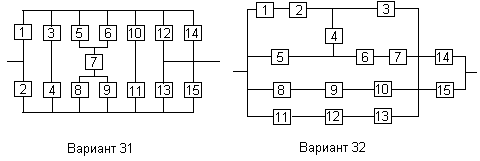
Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов). Резервирование отдельных элементов или групп элементов осуществляется идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются идеальными.
На схемах обведенные пунктиром m элементов являются функционально необходимыми из n параллельных ветвей.
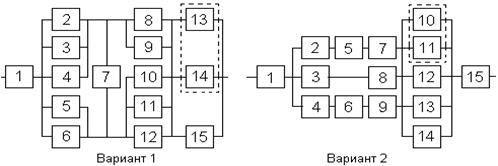
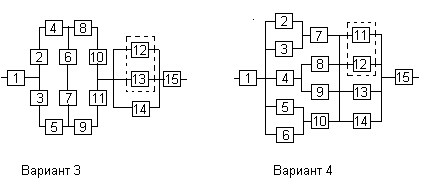
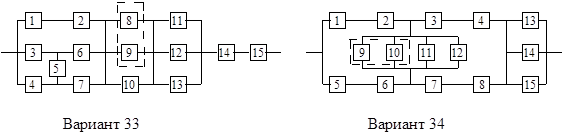
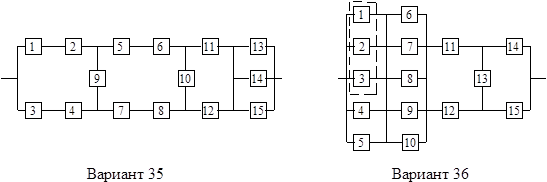
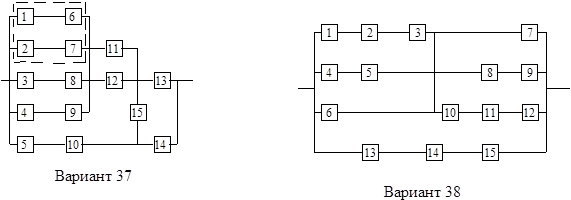
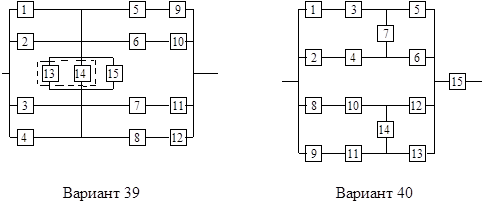
7. ПРИМЕР РАСЧЕТА НАДЕЖНОСТИ
Структурная схема надежности приведена на рис 7.1. Значения интенсивности отказов элементов даны в 
1/ч.
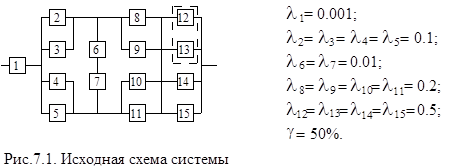
1. В исходной схеме элементы 2 и 3 образуют параллельное соединение. Заменяем их квазиэлементом А. Учитывая, что 
, получим
. (7.1)
2. Элементы 4 и 5 также образуют параллельное соединение, заменив которое элементом В и учитывая, что
, получим
. (7.2)
3. Элементы 6 и 7 в исходной схеме соединены последовательно.Заменяем их элементом С, для которого при
. (7.3)
4. Элементы 8 и 9 образуют параллельное соединение. Заменяем их элементом D, для которого при 
, получим
. (7.4)
5. Элементы 10 и 11 с параллельным соединением заменяем элементом Е , причем, так как 
, то
(7.5)
6. Элементы 12 , 13 , 14 и 15 образуют соединение “2 из 4”,которое заменяемэлементомF.Таккак
,то для определения вероятности безотказной работы элемента F можно воспользоваться комбинаторным методом (см. раздел 3.3):
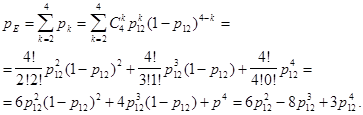(7.6)
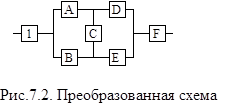
7. Преобразованная схема изображена на рис. 7.2.
8. Элементы A,B,C,D и Е образуют (рис. 7.2) мостиковую систему, которую можно заменить квазиэлементом G. Для расчета вероятности безотказной работы воспользуемся методом разложения относительно особого элемента (см. раздел 3.4), в качестве которого выберем элемент С.Тогда
(7.7)
где 
- вероятность безотказной работы мостиковой схемы при абсолютнонадежномэлементеС(рис. 7.3,а), 
- вероятность безотказной работы мостиковой схемы при отказавшем элементе С (рис. 7.3,б).
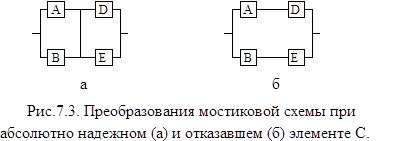
Учитывая, что 
, получим
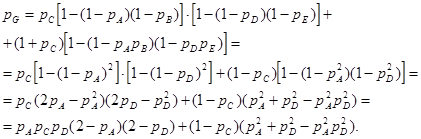(7.8)
9.После преобразований схема изображена на рис. 7.4.
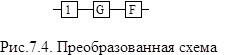
10.В преобразованной схеме (рис. 7.4) элементы 1, G и F образуют последовательное соединение. Тогда вероятность безотказной работы всей системы
(7.9)
11.Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работыэлементов с 1 по 15 (рис. 7.1) подчиняются экспоненциальному закону:
(7.10)
12.Результаты расчетов вероятностей безотказной работы элементов 1 - 15 исходной схемы по формуле (7.10) для наработки до 
часовпредставлены в таблице 7.1.
13.Результаты расчетов вероятностей безотказной работы квазиэле-ментов A, B, C,D,E, F и G по формулам (7.1) - (7.6) и (7.8) также представлены
29-04-2015, 03:09