В разном труде, службе, на занятиях и учениях, воин осуществляет определённую познавательную деятельность. Он усваивает разнообразные знания, развивает навыки, приобретает умение в работе с техникой, оружием, приборами, у него формируется представление о характере современного боя и т.д. Вместе с тем он трудится и развивается физически. Познавательная деятельность и физический труд, учение и бой - всё это осуществляется на основе психических, познавательных процессах и психофизиологических реакциях. Поэтому, принято сочетать любой вид деятельности, в том числе и каждый вид боя, имеет свою психологическую характеристику.
Боевая учёба составляет значительную часть воинской службы. Воин овладевает политическими, специальными военно-техническими знаниями, а также математическими, изучает уставы, инструкции, познаёт армейскую жизнь, у него формируются прочные знания, навыки, умения и привычки.
Бой как всякая сложная воинская деятельность предъявляет к психике в целом и к различным сторонам её своеобразные требования. Успех боевой ратно-трудовой познавательной деятельности, прежде всего, зависит от: политической сознательности, активности, дисциплинированности; от умения мастерски владеть оружием и техникой в бою. Успех во многом зависит и от того, насколько и как развиты органы чувств человека, совершенна и точна его реакция, развито ощущение, внимание, память, мышление и другие психические, познавательные процессы.
Отсюда непреложный практический вывод, в ходе боевой гуманитарной педагогической подготовки, необходимо наряду и на основе формирования боевых, моральных качеств, вооружения воинов знаниями, умениями и навыками, развивать у солдат, сержантов психические, познавательные процессы, способности.
Следует иметь ввиду, что каждый психический процесс носит личностный характер: в нём неизбежно отражается личность с её особенностями. Ощущение, представление, память могут быть только ощущениями, представлениями, памятью и конкретной и определённой личности и в связи с этим они обладают личностными особенностями, то есть на психических процессах обязательно лежит отпечаток свойства личности. На всех этапах и в каждом акте усвоения учебного материала слушателем функционирует все психические процессы, в единстве проявляется свойства и состояния личности. [18, с.78]
Одним из главных направлений формирования у воинов необходимых способностей является максимальное приближение их учебной деятельности к боевым действиям войск. Известно, что возникающие иногда в боевой обстановке ошибочные мысли и эстетические чувства и эмоциональные состояния могут быть причиной появления у воинов образов непроизвольного воображения, отрицательно воздействующих на его поведение. Чтобы такие чувства и мысли не возникали, воин должен быть приучен активно действовать в сложных, трудных и опасных условиях современного боя ещё в мирное время. Научить воина овладеть своим воображением можно лишь в том случае, если он получить большой опыт самостоятельных действий в подобных условиях в процессе боевой подготовки, и особенно в ходе полевой, морской и воздушной выучки войск. Воображение неизбежно вызывает положительные или отрицательные психические состояния. Знание и учёт общих и частных закономерностей психических процессов, особенностей их протекания у каждого воина необходимых для успешной организации процессов ратного труда, обучения, воспитания и психологической подготовки.
1.4
Психологическая характеристика математических способностей военнослужащих и их природных предпосылок
В связи с проблемой формирования и развития способностей следует указать, что целый ряд исследований психологов направлен на выявление структуры способностей военнослужащих к различным видам деятельности. При этом под способностями понимается комплекс индивидуально - психологических особенностей человека, отвечающих требованиям данной деятельности и являющиеся условием успешного выполнения. Таким образом, способности - сложное, интегральное, психическое образование, своеобразный синтез свойств, или, как их называют компонентов.
Общий закон образования способностей состоит в том, что они формируются в процессе овладения и выполнения тех видов деятельности, для которых они необходимы. [13, с.89]
Говоря о математических способностях как особенностях умственной деятельности военнослужащих, следует, прежде всего, указать на несколько распространенных заблуждений.
Во-первых, многие считают, что математические способности заключаются, прежде всего, в способности к быстрому и точному вычислению (в частности в уме). На самом деле вычислительные способности далеко не всегда связаны с формированием подлинно математических (творческих) способностей. Во-вторых, многие думают, что способные к математике люди отличаются хорошей памятью на формулы, цифры, числа. Однако, как указывает академик А. Н. Колмогоров, успех в математике меньше всего основан на способности быстро и прочно запоминать большое количество фактов, цифр, формул. Наконец, считают, что одним из показателей математических способностей является быстрота мыслительных процессов. Особенно быстрый темп работы сам по себе не имеет отношения к математических способностям, можно работать медленно и неторопливо, но в то же время вдумчиво, творчески, успешно продвигаясь в усвоении математики.
Хотя математические способности и не были предметом специального рассмотрения в трудах Б.М.Теплова, однако ответы на многие вопросы, связанные с их изучением, можно найти в его работах, посвященных проблемам способностей. [11, с.238]
Наиболее ярко роль общих способностей продемонстрирована в работе «Ум полководца». Остановимся на рассмотрении основных положений этой работы, поскольку они могут быть использованы при изучении других видов способностей, связанных с мыслительной деятельностью, в том числе и математических способностей. Проведя глубокое изучение деятельности полководца, Б.М.Теплов показал, какое место в ней занимают интеллектуальные функции. Они обеспечивают анализ сложных военных ситуаций, выявление отдельных существенных деталей, способных повлиять на исход предстоящих сражений. Именно способность к анализу обеспечивает первый необходимый этап в принятии верного решения, в составлении плана сражения. Вслед за аналитической работой наступает этап синтеза, позволяющего объединить в единое целое многообразие деталей. По мнению Б.М.Теплова, деятельность полководца требует равновесия процессов анализа и синтеза, при обязательном высоком уровне их развития.
Важное место в интеллектуальной деятельности полководца занимает память. Совсем не обязательно, чтобы она была универсальной. Гораздо важнее, чтобы она обладала избирательностью, то есть удерживала, прежде всего, необходимые, существенные детали. В качестве классического примера такой памяти Б.М.Теплов приводит высказывания о памяти Наполеона, который помнил буквально все, что имело непосредственное отношение к его военной деятельности, начиная от номеров частей и кончая лицами солдат. При этом Наполеон был неспособен запоминать бессмысленный материал, но обладал важной особенностью мгновенно усваивать то, что подчинялось классификации, определенному логическому закону.
Б.М.Теплов приходит к выводу, что «умение находить и выделять существенное и постоянная систематизация материала - вот важнейшие условия, обеспечивающие единство анализа и синтеза, то равновесие между этими сторонами мыслительной деятельности, которые отличают работу ума хорошего полководца». Наряду с выдающимся умом полководец должен обладать определенными личностными качествами. Это, прежде всего мужество, решительность, энергия, то есть то, что применительно к полководческой деятельности принято обозначать понятием «воля». Не менее важным личностным качеством является стрессоустойчивость. Эмоциональность талантливого полководца проявляется в сочетании эмоции боевого возбуждения и умении собраться, сосредоточиться. [11, с.67]
Особое место в интеллектуальной деятельности полководца Б.М.Теплов отводил наличию такого качества, как интуиция. Он анализировал это качество ума полководца, сравнивая его с интуицией ученого. Между ними существует много общего. Основное же отличие, по мнению Б.М.Теплова, состоит в необходимости для полководца принятия срочного решения, от которого может зависеть успех операции, в то время как ученый не ограничен временными рамками. Но и в том и другом случае «озарению» должен предшествовать упорный труд, на основе которого и может быть принято единственно верное решение проблемы.
Подтверждения положениям, проанализированным и обобщенным Б.М.Тепловым с психологических позиций, можно обнаружить в работах многих выдающихся ученых, в том числе и математиков. Так, в психологическом этюде «Математическое творчество» Анри Пуанкаре подробно описывает ситуацию, при которой ему удалось сделать одно из открытий. Этому предшествовала долгая подготовительная работа, большой удельный вес в которой составлял, по мнению ученого, процесс бессознательного. За этапом «озарения» необходимо следовал второй этап - тщательной сознательной работы по приведению в порядок доказательства и его проверке. А.Пуанкаре пришел к выводу, что важнейшее место в математических способностях занимает умение логически выстроить цепь операций, которые приведут к решению задачи. Казалось бы, это должно быть доступно любому способному логически мыслить человеку. Однако далеко не каждый оказывается способным оперировать математическими символами с той же легкостью, что и при решении логических задач. [11, с.28]
Для математика недостаточно иметь хорошую память и внимание. По мнению Пуанкаре, людей, в том числе и военнослужащих, способных к математике, отличает умение уловить порядок, в котором должны быть расположены элементы, необходимые для математического доказательства. Наличие интуиции такого рода - есть основной элемент математического творчества. Одни люди не владеют этим тонким чувством и не обладают сильной памятью и вниманием и поэтому не способны понимать математику. Другие обладают слабой интуицией, но одарены хорошей памятью и способностью к напряженному вниманию и потому могут понимать и применять математику. Третьи владеют такой особой интуицией и даже при отсутствии отличной памяти могут не только понимать математику, но и делать математические открытия.
Для того, чтобы понять, какие качества еще требуются для достижения успехов в математике, исследователями анализировалась математическая деятельность: процесс решения задач, способы доказательств, логических рассуждений, особенности математической памяти. Этот анализ привел к созданию различных вариантов структур математических способностей, сложных по своему компонентному составу. При этом мнения большинства исследователей сходились в одном - что нет и не может быть единственной ярко выраженной математической способности - это совокупная характеристика, в которой отражаются особенности разных психических процессов: восприятия, мышления, памяти, воображения.
Среди наиболее важных компонентов математических способностей выделяются специфическая способность к обобщению математического материала, способность к пространственным представлениям, способность к отвлеченному мышлению. Некоторые исследователи выделяют также в качестве самостоятельного компонента математических способностей математическую память на схемы рассуждений и доказательств, методы решения задач и принципы подхода к ним.
Исследование математических способностей военнослужащих включает в себя и решение одной из важнейших проблем - поиска природных предпосылок, или задатков, данного вида способностей. К задаткам относятся врожденные анатомо-физиологические особенности военного, которые рассматриваются как благоприятные условия для развития способностей. Долгое время задатки рассматривались как фактор, фатально предопределяющий уровень и направление развития способностей. Классики отечественной психологии Б.М.Теплов и С.Л.Рубинштейн научно доказали неправомерность такого понимания задатков и показали, что источником развития способностей является тесное взаимодействие внешних и внутренних условий. Выраженность того или иного физиологического качества ни в коей мере не свидетельствует об обязательном развитии конкретного вида способностей. Оно может являться лишь благоприятным условием для этого развития. Типологические свойства, входящие в состав задатков и являющиеся важной их составляющей, отражают такие индивидуальные особенности функционирования организма, как предел работоспособности, скоростные характеристики нервного реагирования, способность перестройки реакции в ответ на изменение внешних воздействий. [14, с.98]
Математические способности очень сложны и многогранны по своей структуре. И, тем не менее, выделяются как бы два основных типа людей, в том числе и военнослужащих, с их проявлением - это «геометры» и «аналитики». В истории математики яркими примерами этого могут являться такие имена, как Пифагор и Евклид (крупнейшие геометры), Ковалевская и Клейн (аналитики, создатели теории функций). В основе такого деления лежат, прежде всего, индивидуальные особенности восприятия действительности, в том числе и математического материала. Оно определяется не предметом, над которым работает математик: аналитики и в геометрии остаются аналитиками, тогда как геометры любую математическую реальность предпочитают воспринимать образно. В этой связи уместно привести высказывание А.Пуанкаре: «Отнюдь не обсуждаемый ими вопрос заставляет их использовать тот или другой метод. Если часто об одних говорят что они аналитики, а других называют геометрами, то это не мешает тому, что первые остаются аналитиками, даже когда занимаются вопросами геометрии, в то время как другие являются геометрами, даже если занимаются чистым анализом». [13, с.72]
В военной практике при работе с военнослужащими эти различия проявляются не только в разной успешности овладения разными навыками, но и в предпочтительном отношении к принципам решения тех или иных военных задач. Одни военнослужащие любые задачи стремятся решить с помощью «формул», логического рассуждения, другие по возможности используют пространственные представления. Причем эти различия являются, весьма устойчивыми. Конечно, среди военнослужащих встречаются и такие, у которых наблюдается определенное равновесие этих характеристик. Они одинаково ровно овладевают всеми разделами математического мышления, используя при этом разные принципы подхода к решению разных задач, связанных с спецификой их военной службы и деятельности.
Таким образом, проведенный анализ математических способностей военнослужащих позволил подтвердить наличие определенного сочетания психологических и психофизиологических факторов, составляющих благоприятную основу для развития математических способностей военнослужащих. Это касается как общих, так и специальных моментов в проявлении данного вида способностей.
2 Эмпирическое исследование математических способностей военнослужащих и их природных предпосылок
2.1 Организация и методика исследования
Предметом исследования являются математические способности военнослужащих и их природных предпосылки.
Объектом исследования являются военнослужащие 120-ой стрелковой дивизии города Минска. В эксперименте приняли участие 15 военнослужащих.
Целью исследования было определить психологическую характеристику математических способностей военнослужащих и их природные предпосылки.
В задачу исследования входило:
· изучение литературы (психолого-дидактический, методический и др.) с целью выяснения содержания понятия математических способностей по математике;
· диагностировать одновременно уровень развития продуктивного математического мышления (открытие новых отношений) и репродуктивного математического мышления военнослужащих (нахождение решения при помощи применения знаний).
Для решения названных задач необходимо изучить методики, соответствующих особенностям и целям исследования.
В качестве тестового материала были использованы задачи, разработанные А. Г. Гайштутом, направленные на формирование у учащихся таких умственных операций, как анализ, синтез, аналогия, обобщение.
С точки зрения автора, «Математика, как известно, наука доказательная, или дедуктивная. Но доказательство открывается с помощью правдоподобного рассуждения, с помощью догадки. Два типа рассуждения - доказательное и правдоподобное - дополняют друг друга».
Задачи, предложенные А. Г. Гайштутом, сформулированы на основе материала из курса математики с 4 по 10 класс и состоят из 5 серий: 4 класс, 5 класс, 6-7 класс, 8 класс, 9-10 класс, итого - 15 задач. Решение задач каждого типа предполагает знание учебного материала, но помимо того способность к мысленному обнаружению отношений между пространственными и знаковыми элементами условий задачи и умения производить математические операции с математическими структурами. Таким образом, задачи, предложенные А. Г. Гайштутом, могут быть использованы для диагностики уровня развития мышления военнослужащих, мыслительной способности оперировать абстрактными структурами на математическом материале.
Примененные в исследовании данной методики даст возможность, во-первых, определить роль познавательных процессов в деятельности военнослужащих, а также выявить особенности математических способностей военнослужащих.
2.2 Анализ результатов
В данные задачи входят 4 элемента, один из которых неизвестен. Требуется найти неизвестный элемент. Решение может быть найдено только тогда, когда будет решена вспомогательная задача: выделены отношения элементов начальных условий задачи. Между элементами «электричество» и XIII отношение тождества: число букв в слове «электричество» равно 13, между элементами «электричество» и «математик» - отношение различия: разное число букв. Следовательно, требуется, чтобы неизвестное находилось в отношении тождества с элементом «математик» и в том же отношении количественного различия с элементом XIII, как элементы «математик» и «электричество». Неизвестный элемент - число IX. Следовательно, испытуемый должен произвести операции сравнения элементов, выделить тип отношений - количественные различия, и сделать умозаключение по аналогии. Как видно, отношения между элементами задачи арифметические, от испытуемого требуется знание цифровых обозначений и умение читать и считать, а также владение арифметическими действиями. Следовательно, данная задача соответствует уровню подготовки школьника 4-го класса. Тем самым, несмотря на то, что в задаче присутствует конкретный материал и для его решения требуются стандартные знания и умения, успешно решить эту задачу можно, только обладая определенным уровнем развития мыслительной способности, оперируя с символическими (пространственно-знаковыми) структурами. Следовательно, задачи удовлетворяют выдвинутому требованию: диагностировать одновременно уровень развития продуктивного математического мышления (открытие новых отношений) и репродуктивного математического мышления военнослужащих (нахождение решения при помощи применения знаний). Поскольку материал теста должен соответствовать учебной программе средней школы, тест был разбит на 5 субтестов: 1) субтест для 4 класса, 2) субтест для 5 класса, 3) субтест для 6 класса, 4) субтест для 7- 8 классов и субтест для 9-10 классов.
Приведем результаты стандартизации теста математических аналогий (ТМА).
Военнослужащим, имеющим, по мнению испытуемого, ярко выраженные те или иные математические способности в решении одной из 15 задач, в соответствующие клетки матрицы ставилась оценка «+1», а военнослужащим, которых испытуемый наделял отсутствием математических способностей, ставилась оценка «-1» Данные самооценки вносились в специальную графу.
Таблица 2.1 - Результаты эксперимента
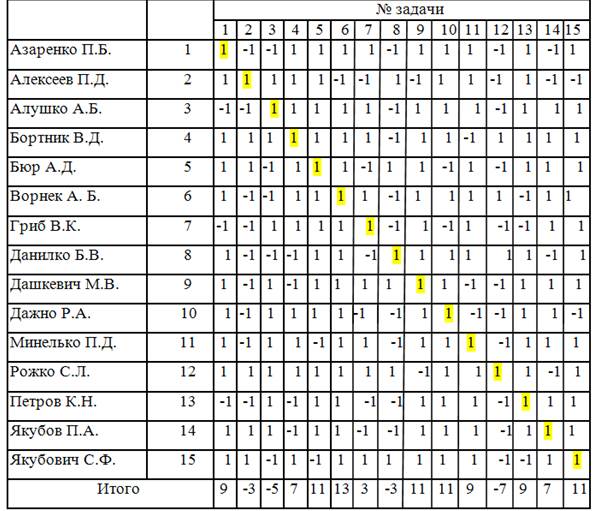
Материалы исследования дозволили охарактеризовать содержание математические способности военнослужащих.
Предлагаемый тест математических аналогий - «Задачи Гайштута» (ТМА) может быть использован для диагностики уровня развития общего интеллекта и математических способностей военнослужащих. Тест обладает достаточной внутренней и внешней валидноетью. Успешность выполнения теста связана с уровнем развития способности к мысленному решению задач, понятийного и пространственного мышления. Задачи теста обладают высокой однородностью.
9-09-2015, 20:01
