Реферат
Социальные различия имущественной обеспеченности населения в российских регионах
(на основе данных Госкомстата РФ)
Москва, 2008
Содержание
Введение
Выбор методов
Описание использованных данных
Анализ и интерпретация
Список использованных источников
Приложение. Порядок выполнения анализа в SPSS
Введение
Проблема изучения различий в материальной обеспеченности населения России в региональном аспекте является весьма актуальной для нашей страны. Дело в том, что огромная территория страны подразделена на множество регионов, каждый из которых имеет своё управление, свой климат, природные богатства, свой экономический и социальный потенциал, даже своё законодательство по отдельным вопросам. При этом для обеспечения территориально-административной целостности страны выгодно было бы, чтобы между российскими регионами не существовало чрезмерных различий в экономическом развитии и уровне жизни населения. Исключительная поляризация регионов по социально-экономическим показателям приводит к нарушению различных миграционных балансов, появлению устойчиво отсталых регионов, перенаселению отдельных регионов (например, московский регион) с сопутствующим этим процессам багажом социальных проблем. Кроме прочего, сильная дифференциация между регионами способствует усилению социальной напряжённости, лишает население России понимания того, что они живут в единой стране (вспомним хотя бы многочисленные шутки и анекдоты относительно того, что современная Москва – это государство в государстве и москвичи, порой, не понимают, что за пределами Москвы есть ещё «какая-то Россия»).
Поэтому я воспользовавшись процедурами кластерного анализа решила посмотреть, можно ли разбить российские регионы на однородные группы по ряду показателей, характеризующих обеспеченность и неравенство населения по денежным доходам (например, коэффициенты неравенства доходов – Джини и коэффициент фондов, соотношения различных показателей доходов с величиной прожиточного минимума (далее – с ПМ), численности населения с доходами, ниже ПМ). Ясно, что в России есть «богатые» и «бедные» регионы. Однако, поскольку прожиточный минимум в бедных регионах, как правило ниже ПМ в богатых, можно предположить, что в этом плане уровень жизни в первых и вторых может и не слишком различаться. Ответ на этот вопрос (есть ли обособленные группы регионов или нет) и поможет нам дать проводимый далее анализ.
Естественно, что в данной работе используются данные региональной статистики, которые являются большой частью всей государственной статистики. Положительным моментом, связанным с использованием официальных статистических данных для характеристики уровня жизни населения является «повсеместный охват всей территории страны и единообразная методология и методика получения данных, что важно для межрегиональных сравнений» [2]. Л. А. Беляева отмечает и недостатки, связанные с использованием официальной статистики: недоучёт реальных доходов вследствие их сокрытия населением, условности, связанные с расчётом величины прожиточного минимума (она используется в нашей работе), а также – принципиальный недостаток, связанный с потерей связи опубликованных данных со многими параметрами, которые влияют на положение каждого отдельного индивида. Но в данном случае нас интересуют межрегиональные сопоставления, это во-первых, а во вторых – общие закономерности в развитии регионов, так что от точной оценки доходов тут, конечно, мало что зависит. В работе изучается социально-экономическое положение (прежде всего - дифференциация по доходам) в регионах РФ. Исследуются различия в социально-экономическом положении населения в регионах. На основе статистических исследований Росстата, построена разобрана кластерная модель распределения регионов России по социально-экономическому положению. Методологическая часть содержит краткое описание используемых методов анализа: теоретические аспекты, а также практическое применение для построения статистической модели - группировки регионов России по показателям обеспеченности населения.
Итак, целью данной работы являлось распределение регионов России по однородным группам и установление качественных взаимосвязей между группами регионов с близкими значениями показателей социально-экономического положения. Задача решается с помощью кластерного анализа в системе SPSS.
Выбор методов
При анализе социально-экономических процессов приходится довольно часто сталкиваться с многомерностью их описания. В маркетинге, например, это случается при решении задачи сегментирования рынка, в экономике – при построении типологии стран, в социологии – при анализе мнений респондентов по разным вопросам, в социальной статистике – как сейчас, при изучении регионов, каждый из которых описывается по множеству параметров. Многомерный анализ, куда входит и кластерный анализ - важный количественный инструмент исследования социально-экономических процессов, которые характеризуются большим числом показателей. Название кластерный анализ происходит от английского cluster(гроздь, скопление). Впервые определение кластерного анализа и его описание были даны в 1939 Трионом (Tryon). «Главное назначение кластерного анализа - разбиение множества исследуемых объектов и признаков на однородные в соответствующем понимании группы или кластеры. Это означает, что решается задача классификации данных и выявления соответствующей структуры в ней. Методы кластерного анализа можно применять в самых различных случаях, даже в тех случаях, когда речь идет о простой группировке, в которой все сводится к образованию групп по количественному сходству» [9].
Кластерный анализ позволяет рассматривать достаточно большой объем информации и резко сокращать, сжимать большие массивы экономической информации, делать их компактными и наглядными, то есть, в нашем случае – рассматривать не каждый регион в отдельности, а группы регионов, сравнивать их между собой.
Для проведения кластерного анализа используются различные компьютерные программы. Процесс кластерного анализа данных в системе SPSS включает в себя следующие этапы:
- Ввод данных в систему;
- Преобразование данных, адекватное методу кластерного анализа;
- Визуализацию данных с помощью различных типов графиков;
- Реализацию алгоритма метода кластерного анализа;
- Вывод результатов анализа в виде графиков и электронных таблиц с численной и текстовой информацией;
- Интерпретацию полученных результатов.
Общий принцип кластерного анализа (КА) такой. Если некая совокупность содержит набор объектов, свойства которых описываются с помощью некоторых признаков, то задача КА заключается в разбиении совокупности объектов на группы, такие, чтобы каждый объект входил только в одну группу, объекты из одной и той же группы были похожи друг на друга, а объекты из разных групп имели заметные различия. Группы сходных друг с другом объектов называют кластерами. Разбивку исходной совокупности на кластеры называют кластерным решением [4, 5].
Как правило, общее количество кластеров и их примерный состав заранее не известны. Для отыскания и исследования кластеров применяются вычислительные алгоритмы, использующие различные способы измерения сходства объектов и групп объектов и различные схемы поиска кластерного решения. В данной работе используются алгоритмы кластерного анализа иерархический и k-средних. Их взаимодействие такое. С помощью иерархического анализа мы проводим предварительный анализ и находим, на какое число кластеров можно было бы разбить всю совокупность регионов. После этого мы проводим кластерный анализ методом k-средних, задав разбиение на выбранное число кластеров. Такая схема рекомендуется в некоторых методических публикациях [5].
Важно отметить ещё такой момент. Довольно часто признаки имеют разный масштаб и разные единицы измерения. Признак, имеющий большую изменчивость (большую дисперсию), вносит больший вклад в величину расстояния между объектами, чем другие признаки при проведении кластерного анализа. И наоборот: признаки с малой изменчивостью (малой дисперсией) фактически не влияют на величины. Поэтому при больших различиях изменчивости рекомендуется провести стандартизацию данныхи попробовать найти кластерное решение на основе стандартизированных данных. Стандартизация заключается в вычитании из значения признака его среднего значения и делении результата на стандартное отклонение признака. Стандартизированные значения иногда также называют Z-вкладами [7].
Описание использованных данных
В данной работе используются данные из сборника Госкомстата «Социальное положение и уровень жизни населения России. 2005» за 2004 год [1]. То есть, сборник выпущен в 2005 году, но, поскольку статистическому учёту на такой большой территории как Россия присуще некоторое запаздывание, данные относятся к 2004 году.
Данный вид информации собирается Федеральной службой государственной статистики (Росстатом). Как следует из методологических пояснений к данным, «главной задачей Росстата является удовлетворение потребностей органов власти и управления, средств массовой информации, населения, научной общественности, международных организаций в разнообразной, объективной и полной информации … Международная экспертиза признала статистические данные Федеральной службы государственной статистики надежными … Сбор статистических данных проводится органами государственной статистики в соответствии с Федеральной программой статистических работ, ежегодно утверждаемой Росстатом по согласованию с Правительством Российской Федерации. Обследование организовано во всех субъектах Российской Федерации» [1]
Таким образом, в нашем распоряжении имеются данные о социально-экономической обстановке по регионам Российской Федерации. Указанный уровень обобщения (регион) будет представлять исходные данные для построения кластерной модели в нашей работе. См. пример данных в таблице 1. Полностью данные приведены в сборнике [1].
Таблица 1 «Показатели социально-экономической дифференциации регионов РФ за 2004 г» (фрагмент)
| Регион | Коэффициент Джини | Коэффициент фондов | Соотношение среднедушевых денежных доходов с величиной ПМ, % | Соотношение среднемесячной начисленной зарплаты с величиной ПМ, % | Соотношение среднего размера назначенных месячных пенсий с величиной ПМ, % | Численность населения с денежными доходами ниже величины ПМ |
Белгородская область |
0,352 |
10,2 |
244,2 |
263,o |
125,2 |
21,2 |
| Брянская обл. область | 0,355 | 10,3 | 223,2 | 209,2 | 125,2 | 25,3 |
| … | … | … | … | … | … | … |
| Санкт-Петербург | 0,410 | 15,3 | 381,3 | 267,3 | 106,2 | 13,5 |
Единицей наблюдения является регион, а показателями – статистика по этому региону, полученная на основе исследований. Хотя данные присутствовали почти по всем российским регионам, в анализе была использована информация только по 70 из них, включая Москву и Санкт-Петербург (о причинах этого см. ниже).
Регион характеризуется 6 показателями. По результатам кластерного анализа можно ожидать появление «богатых» и «бедных» регионов (или же регионов с высоким и низким уровнем жизни). В данном случае нас интересует типовые группы регионов рассматриваемых по схожим социально-экономическим показателям.
Для работы с базой данных и статистического анализа используется статистический пакет SPSS 13.0 для Windows. Для обработки в статистическом пакете информация должна быть организована в особом виде. Традиционным представлением является прямоугольная таблица, матрица данных. В исходных данных представлена статистика по регионам, а также – информация по группам регионов (федеральным округам) и России в целом. Для того чтобы обработать данные в статистическом пакете, нужно привести их к нужной структуре т.е. оставить только информацию по регионам.
В файле данных информация по показателям социально-экономического положения представлена переменными (информация об одном и том же показателе записывается в один столбец, а регион формирует строку файла данных). Список переменных с их краткой характеристикой из [1] представлен в таблице 2.
Таблица 2 «Список переменных»
| № | Имя | Тип | Описание | Смысл показателя |
| 1 | Region | Номинальный | Регион | Регион |
| 2 | Gini | Числовой | Коэффициент Джини | (индекс концентрации доходов / заработной платы) Характеризует степень отклонения линии фактического распределения общего объема доходов /заработной платы от линии их равномерного распределения. |
| 3 | Fond | Числовой | Коэффициент Фондов | Коэффициент дифференциации доходов / заработной платы. Характеризует степень соц. расслоения и определяется как соотношение между средними уровнями денежных доходов / заработной платы 10% процентов населения (работников) с самыми высокими доходами и 10 % процентов населения (работников) с самыми низкими доходами / заработной платой |
| 4 | Sdohod | Числовой | Соотношение среднедушевых денежных доходов с величиной ПМ, % | Характеризует общий уровень денежных доходов населения относительно установленного прожиточного минимума |
| 5 | Szarplata | Числовой | Соотношение среднемесячной начисленной зарплаты с величиной ПМ, % | Характеризует общий уровень заработной платы населения относительно установленного прожиточного минимума |
| 6 | Spensii | Числовой | Соотношение среднего размера назначенных месячных пенсий с величиной ПМ, % | Характеризует общий уровень пенсий населения относительно установленного прожиточного минимума. |
| 7 | ChislMin | Числовой | Численность населения с денежными доходами ниже величины ПМ | Определяется на основе данных о распределении населения по величине среднедушевых денежных доходов и является результатом их соизмерения с величиной прожиточного минимума |
На практике большую проблему представляют пропущенные значения (пункты, по которым отсутствует информация). Связано это с тем, что нельзя отнести регион к какому либо кластеру, не имея полной информации о нем. В данной таблице пропусков довольно мало. Информация полностью отсутствует по Чеченской Республике. Статистические исследования в этом регионе не проводились в связи с проходившими на территории Чечни военными действиями. Также, вне зоны нашего внимания останутся такие регионы как Архангельская область, Пермская область, Тюменская область, Красноярский край, Иркутская область и Читинская область из-за частичного или полного отсутствия статистических данных. По остальным регионам, включая Москву и Петербург, все данные находятся в нашем распоряжении. Поэтому в дальнейшем исключим выше перечисленные субъекты из рассмотрения, и модель будем строить на базе информации о 70 регионах РФ.
Анализ и интерпретация
В задачи работы входит построение кластерной модели социально-экономического положения по регионам РФ. Требуется выделить группы регионов, имеющих схожую, однородную социально-экономическою обстановку. Таким образом, исходными данными должна являться статистика показателей социально-экономического положения на региональном уровне (по всем регионам РФ).
Описательная статистика. Для начала работы стоит провести разведочный анализ с целью определения перспектив кластеризации. Прибегнем к возможностям SPSS и получим описательные статистики показателей социально-экономического положения.
Таблица 3 «Описательная статистика показателей»
| Количество | Минимум | Максимум | Среднее | Стандартное отклонение | |
| Gini | 70 | ,314 | ,578 | ,36346 | ,036434 |
| Fond | 70 | 7,8 | 44,0 | 11,430 | 4,4475 |
| Sdohod | 70 | 105,1 | 674,0 | 231,597 | 73,1439 |
| Szarplata | 70 | 168,1 | 309,4 | 234,240 | 36,9582 |
| Spensii | 70 | 80,7 | 132,6 | 111,811 | 13,0245 |
| ChislMin | 70 | 13,5 | 73,0 | 26,624 | 10,0924 |
Наиболее важным показателем для нас является стандартное отклонение. Чем выше стандартное отклонение величины (чем больше ее изменчивость), тем больше эта переменная будет оказывать влияние на результаты кластеризации. Мы видим, например что переменные Sdohodили Szarplataимеют наибольшее стандартное отклонение и возможно разделение регионов на группы именно по этим признакам. Практически большее стандартное отклонение означает, что между регионами существует большая дифференциация по данным показателям: в какой-то части регионов показатели малы, а в какой-то части регионов наоборот велики. Таким образом, справедливо ожидать, что показатели с большей «дифференцирующей способностью» (большей дисперсией) окажут большее влияние на результат кластеризации [4, 5]
Видно, что, как и для многих экономических показателей, чем меньше среднее показателя, тем меньше стандартное отклонение этого показателя. Связано это с невозможностью переменных принимать отрицательные значения. Это значит, что наибольшее влияние на результаты кластеризации окажут переменные с большей средней величиной.
Так же большое подспорье в оценке перспектив кластеризации окажут гистограммы абсолютных или стандартизированных значений по тем переменным по которым она проводиться. Далее мы будем рассматривать только стандартизированные значения, в связи с тем, что стандартные отклонения слишком различны. Стандартизация показателей проводилась с помощью меню SPSSAnalyze – DescriptiveStatistics – Descriptives с установкой флажка стандартизации. Изучим гистограммы наших показателей.
При анализе гистограммы Коэффициента Джини мы видим, что все регионы отчетливо делятся на две группы. Причем одна из этих групп крайне велика и туда входит большая часть всех регионов РФ.
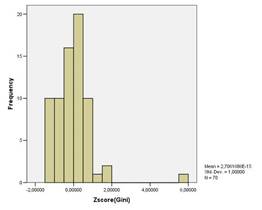
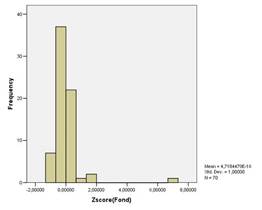

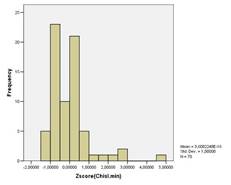
Анализ гистограмм для коэффициента фондов, численности населения с доходами, ниже ПМ и соотношения денежных доходов с ПМ выявил аналогичные распределение регионов как и для коэффициента Джини.
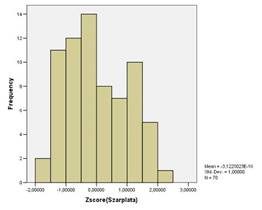

А вот анализ гистограмм Szarplataи Spensii не выявил очевидного деления на какие-либо группы регионов.
Стоит также рассмотреть и корреляции всех показателей.
Таблица 4 «Матрица корреляций показателей»
| Gini | Fond | Sdohod | Szarplata | Spensii | ChislMin | |
| Gini | 1 | ,953(**) | ,872(**) | ,455(**) | -,225 | -,384(**) |
| Fond | ,953(**) | 1 | ,881(**) | ,370(**) | -,257(*) | -,301(*) |
| Sdohod | ,872(**) | ,881(**) | 1 | ,599(**) | -,046 | -,658(**) |
| Szarplata | ,455(**) | ,370(**) | ,599(**) | 1 | -,069 | -,668(**) |
| Spensii | -,225 | -,257(*) | -,046 | -,069 | 1 | -,250(*) |
| ChislMin | -,384(**) | -,301(*) | -,658(**) | -,668(**) | -,250(*) | 1 |
Как следует из справочной информации по пакету SPSS, звёздочками отмечены значимые корреляции, то есть, те, на которые имеет смысл обращать внимание. Исследовав таблицу корреляций мы можем заметить, что Коэффициент фондов и Коэффициент Джини дают нам крайне близкую информацию (корреляция 0,953) что в свою очередь позволяет нам вместо обоих показателей воспользоваться одним. В данной ситуации более предпочтительным для работы является коэффициент фондов так как он в свою очередь обладает большим относительным разбросом. Об этом нам может сказать коэффициент вариации (отношение стандартного отклонения переменной к среднему значению этой переменной). У коэффициента Джини он составляет порядка 0,1 а у коэффициентов фондов около 0,389 (в таблицах не показано).
Иерархическая кластеризация. После изучения полученного результата описательной статистики показателей социально-экономического положения было установлено, что ряд переменных не стоят нашего внимания, а именно – коэффициент Джини.
Было решено провести серию пробных разбиений наблюдений на 2, 3 и так далее кластеров, чтобы установить переменные либо данные, которые играют малозаметную роль в разбиении регионов на кластеры. При этом воспользуемся методом k-средних.
При первом же разбиении на 2 кластера, мы можем судить о том, что город Москва явно превзошел все остальные регионы по уровню социально-экономического развития. И при любом количестве кластеров Москва всегда будет отделяться в отдельный кластер. Поэтому целесообразнее всего будет исключить Москву из рассмотрения в работе, ибо дальнейшее ее рассмотрение не поможет нам объективно взглянуть на общую социально-экономическую обстановку в целом по России. То есть далее мы будем рассматривать только 69 регионов.
Кластерный анализ с разбиением на 3 кластера создал у нас две достаточно большие группы: 24 и 38 регионов и одну маленькую (7 регионов). В самую малочисленную группу попали самые худшие по показателям регионы с достаточно малыми доходами, зарплатами и большой прослойкой населения, доходы которых явно меньше прожиточного минимума. Такие регионы как Ингушетия, Калмыкия, республика Тыва. В основном это регионы с крайне низким уровнем жизни и не развитой экономикой.
Две другие группы оказались более подкованными в этом плане. Во вторую группу попали такие регионы как Тамбовская, Тульская области республика Саха. Лучший результат же показали регионы первого кластера. Самые доходные и социально обеспеченные. Такие как Московская область, Мурманская и Вологодская области.
Далее приводится дендрограмма (график объединения) для иерархического кластерного анализа с оставшимися переменными. Из нее будет видно на каких расстояниях объекты объединяются в кластеры, из этого можно будет сделать вывод на сколько кластеров разбить всю совокупность.

Красной линией на дендрограмме мы отметили один из вариантов кластерного решения, который предусматривает разбиение на 6 кластеров. Это решение даёт следующие центры кластеров:
Таблица 6 «Кластерные центры по итогам иерархического анализа»
| Кластер | 1 | 2 | 3 | 4 | 5 | 6 |
| zFond | ,18 | -,32 | -,15 | -,03 | 1,06 | -,70 |
| zSdohod | ,58 | -,25 | -,89 | ,01 | 1,37 | -1,73 |
| zSzarplata | 1,18 | -,35 | -1,23 | ,68 | 1,14 | -1,29 |
| zSpensii. | ,86 | ,36 | -,53 | -1,83 | -,55 | -1,41 |
| zChislMin | -,80 | -,07 | 1,54 | -,21 | -,99 | 4,60 |
Кластеризация методом
k
-средних
. Повторим разбиение на 6 групп с помощью метода k-средних. Таблица 7 показывает, как распределились в итоге регионы по кластерам. Последняя графа показывает расстояние от региона до центра
10-09-2015, 14:56
