Рассчитаем среднегодовой уровень численности безработных:
У=950,4/14=67,9тыс.ч., т.е. за период 1992-2005гг. ежегодно численность безработных составила 67,9 тыс. чел.
Средний абсолютный прирост:
Равен ∆=24,83/13=1,91тыс.чел., т.е. за период с 1992-2005гг. в среднем ежегодно абсолют. прирост численности безработных составил 1,91тыс. чел.
Средний темп роста:
Тр =1,0096 или 100,96% - это говорит о том, что с 1992-2005гг. в среднем ежегодно темп роста безработных составил 100,96%.
Средний темп прироста:
Тпр = 100,96%-100%= 0,96% - с 1992-2005гг. в среднем темп прироста достигал 0,96%.
2. Определение наличия тенденции средних и дисперсии на базе методов: Метод проверки существенности разности средних.
Выдвигаем гипотезу Н0 об отсутствии тенденции, проверка осуществляется на основе кумулятивного t-критерия Стьюдента. Расчетное значение определяется по формуле:
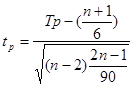, где 
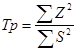Таблица 2. Для расчёта характеристик S2
и Z2
.
| год | безработные-всего, тыс.чел. | S2 | Z2 |
| 1992 | 29,3 | 1488,857 | 1488,857 |
| 1993 | 29,25 | 1492,72 | 2981,58 |
| 1994 | 48,03 | 394,25 | 3375,83 |
| 1995 | 60,06 | 61,24 | 3437,07 |
| 1996 | 66,39 | 2,237 | 3439,3 |
| 1997 | 96,26 | 805,1 | 4244,4 |
| 1998 | 93,59 | 660,71 | 4905,12 |
| 1999 | 84,74 | 284,07 | 5189,18 |
| 2000 | 92,91 | 626,22 | 5815,4 |
| 2001 | 81,26 | 178,87 | 5994,27 |
| 2002 | 69,73 | 3,4 | 5997,67 |
| 2003 | 76,85 | 80,36 | 6078,03 |
| 2004 | 67,9 | 0,000204 | 6078,03 |
| 2005 | 54,13 | 189,22 | 6267,25 |
| итого | 950,4 | 6267,25 | 65291,97 |
| СРЕДН | 67,886 |
Tp = 10,418; tp =4,174
Табличное значение t-критерия Стьюдента для числа степеней свободы df=(n-2)=12 и вероятности 95% составляет 2,1788. Tp >tтабл → гипотеза Н0 о равенстве средних отвергается, расхождение между средними существенно значимо и не случайно, то в ряде динамики существует тенденция средней и, следовательно в исходном временном ряду тенденция имеется.
Метод Фостера – Стюарта.
Кроме определения наличия тенденции явления этот метод позволяет выявить основную тенденцию дисперсии уровней ряда динамики.
1. Сравнивается каждый уровень ряда со всеми предыдущими, при этом
если уi >yi -1 , то Ui =1; Li =0;при уi <yi -1 , то Ui =0; Li =1;
2. Вычисляются значения величин S и d:
S=∑Si , где Si =Ui + Li d=∑di , где di =Ui - Li
Показатель S характеризует тенденцию изменения дисперсии ряда динамики, а показатель d - изменение тенденций в среднем.
3. Проверяется с использованием t-критерия Стьюдента гипотеза о том, можно ли считать случайными разности S-µ и d-0: 
4. Сравниваются расчетные значения ts и td c табличными значениями.
Таблица 3. Для определения Ui и Li .
| год | тыс.чел. | Ui | Li |
| 1992 | 29,3 | 0 | 0 |
| 1993 | 29,25 | 1 | 0 |
| 1994 | 48,03 | 1 | 0 |
| 1995 | 60,06 | 1 | 0 |
| 1996 | 66,39 | 1 | 0 |
| 1997 | 96,26 | 1 | 0 |
| 1998 | 93,59 | 0 | 1 |
| 1999 | 84,74 | 0 | 1 |
| 2000 | 92,91 | 1 | 0 |
| 2001 | 81,26 | 0 | 1 |
| 2002 | 69,73 | 0 | 1 |
| 2003 | 76,85 | 1 | 0 |
| 2004 | 67,9 | 0 | 1 |
| 2005 | 54,13 | 0 | 1 |
Определяем значения S=13 и d=1. По данным таблицы при n=14, µ=4,636, σ1 =1,521, σ2 =2,153. По этим значениям рассчитаем:
ts =(13-4,636)/1,521=5,499 и td =(1-0)/2,153=0,465
Табличное значение tтабл для двустороннего критерия при уровне значимости 0,10 равно tтабл =1,761, т.е. tтабл > td , tтабл < ts → гипотеза об отсутствии тенденции в дисперсии показателя численности безработных отвергается, а в средней - подтверждается.
3. Определение наличия тенденции автокорреляции.
Автокорреляцию измеряют при помощи коэффициента автокорреляции:
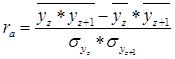, где
σя
и σя+1
-среднеквадратические отклонения рядов
и 
соответственно.
Если значение последнего уровня (yn
) ряда мало отличается от первого (y1
), то сдвинутый ряд можно условно дополнить, принимая yn
=y1
. Тогда yt
=yt
+1
и 
значит формула коэффициента автокорреляции примет вид: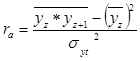 
Таблица 4. Исходные данные и расчет необходимых величин.
| год | ||||
| Числен-ть безраб-х тыс.чел.(yt ) | уровни со сдвигом (yt+1 ) |
 |
yt 2 | |
| 1992 | 29,3 | 29,25 | 857,025 | 858,49 |
| 1993 | 29,25 | 48,03 | 1404,878 | 855,5625 |
| 1994 | 48,03 | 60,06 | 2884,682 | 2306,881 |
| 1995 | 60,06 | 66,39 | 3987,383 | 3607,204 |
| 1996 | 66,39 | 96,26 | 6390,701 | 4407,632 |
| 1997 | 96,26 | 93,59 | 9008,973 | 9265,988 |
| 1998 | 93,59 | 84,74 | 7930,817 | 8759,088 |
| 1999 | 84,74 | 92,91 | 7873,193 | 7180,868 |
| 2000 | 92,91 | 81,26 | 7549,867 | 8632,268 |
| 2001 | 81,26 | 69,73 | 5666,26 | 6603,188 |
| 2002 | 69,73 | 76,85 | 5358,751 | 4862,273 |
| 2003 | 76,85 | 67,9 | 5218,115 | 5905,923 |
| 2004 | 67,9 | 54,13 | 3675,427 | 4610,41 |
| 2005 | 54,13 | 29,3 | 1586,009 | 2930,057 |
| итого | 950,4 | 950,4 | 69392,08 | 70785,83 |
| средн | 67,89 | 4956,58 | 5056,13 |
ra = 0,778
Приводим сопоставление полученного коэффициента автокорреляции с табличным при выборке n=14. При уровне значимости Р=0,05 ra табл =0,335.
Следовательно, ra факт > ra табл , что говорит о наличии автокорреляции в ряду динамики.
Критерий Дарбина - Уотсона.
Выдвигается гипотеза Н0 об отсутствии автокорреляции.
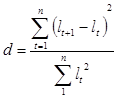
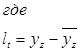
Таблица 5. Для определения величины Дарбина-Уотсона.
| год | тыс.чел. | t | t2 | yt | ytˆ | lt | Lt+1 | Lt2 | Lt+1-lt | (Lt+1-lt)2 |
| 1992 | 29,3 | -13 | 169 | -380,9 | 51,77 | -22,47 | -25 | 504,9 | -2,53 | 6,4 |
| 1993 | 29,25 | -11 | 121 | -321,75 | 54,25 | -25 | -8,7 | 625 | 16,3 | 265,69 |
| 1994 | 48,03 | -9 | 81 | -432,27 | 56,73 | -8,7 | 0,85 | 75,69 | 9,55 | 91,2 |
| 1995 | 60,06 | -7 | 49 | -420,42 | 59,21 | 0,85 | 4,7 | 0,72 | 3,85 | 14,82 |
| 1996 | 66,39 | -5 | 25 | -331,95 | 61,69 | 4,7 | 32,09 | 22,09 | 27,39 | 750,21 |
| 1997 | 96,26 | -3 | 9 | -288,78 | 64,17 | 32,09 | 26,94 | 829,8 | -5,15 | 26,52 |
| 1998 | 93,59 | -1 | 1 | -93,59 | 66,65 | 26,94 | 15,61 | 125,76 | -11,33 | 128,37 |
| 1999 | 84,74 | 1 | 1 | 84,74 | 69,13 | 15,61 | 21,3 | 243,67 | 5,69 | 32,38 |
| 2000 | 92,91 | 3 | 9 | 278,73 | 71,61 | 21,3 | 7,17 | 453,69 | -14,13 | 199,66 |
| 2001 | 81,26 | 5 | 25 | 406,3 | 74,09 | 7,17 | -6,84 | 51,41 | -14,01 | 196,28 |
| 2002 | 69,73 | 7 | 49 | 488,11 | 76,57 | -6,84 | -2,2 | 46,79 | 4,64 | 21,53 |
| 2003 | 76,85 | 9 | 81 | 691,65 | 79,05 | -2,2 | -13,63 | 4,84 | -11,43 | 230,65 |
| 2004 | 67,9 | 11 | 121 | 746,9 | 81,53 | -13,63 | 29,88 | 185,78 | 43,51 | 1893,12 |
| 2005 | 54,13 | 13 | 169 | 703,69 | 84,01 | -29,88 | - | 592,814 | - | - |
| итого | 950,4 | - | 910 | 1130,5 | - | - | - | 3756,83 | - | 5862,9 |
Величина критерия Дарбина – Уотсона D=5862,9/3756,83=1,56
dL =1,08
dU =1,36
Расчитанное значение попадает в отрезок от dU до 4-dU . Следовательно, нет оснований отклонять гипотезу Н0 об отсутствии автокорреляции в остатках.
После того как установлено наличие тенденции в ряду динамики, производится ее описание с помощью методов сглаживания.
4. Выявление основной тенденции.
Метод скользящей средней.
Сначала найдем скользящие средние путем суммирования уровней ряда за каждые 4 года и разделив полученные суммы на 4. Потом найдем центрированные скользящие средние, для чего найдем средние значения из 2 последовательных скользящих средних. И найдем оценки сезонной компоненты.
Таблица 6. Расчет оценок сезонной компоненты.
Безраб-ных, тыс.чел. |
Скольз. Средняя | Центр. Скол.сред |
Оценка сезон комп S | |
| 1 | 48,03 | - | - | - |
| 2 | 60,06 | 67,685 | - | - |
| 3 | 66,39 | 79,075 | 73,38 | -6,99 |
| 4 | 96,26 | 85,245 | 82,16 | 14,1 |
| 5 | 93,59 | 91,875 | 88,56 | 5,03 |
| 6 | 84,74 | 88,125 | 90 | -5,26 |
| 7 | 92,91 | 82,16 | 85,143 | 7,7675 |
| 8 | 81,26 | 80,188 | 81,173 | 0,086 |
| 9 | 69,73 | 73,935 | 77,061 | -7,331 |
| 10 | 76,85 | 67,153 | 70,544 | 6,306 |
| 11 | 67,9 | - | - | - |
| 12 | 54,13 | - | - | - |
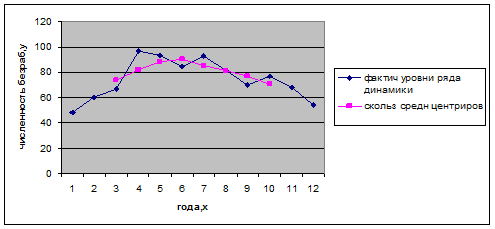
Рис. 1. Динамика численности безработных за 1994-2005гг.
Скользящая средняя дает более или менее плавное изменение уровней.
На графике не проявляется сильно выраженный недостаток скользящих средних. Но в начале и в конце динамического ряда отсутствуют данные, в результате чего становится не совсем ясна закономерность. Это и является минусом данного, наиболее простого из всех остальных метода. Для более точного анализа использую метод аналитического выравнивания.
Метод аналитического выравнивания и определение параметров.
Аналитическое выравнивание ряда динамики имеет задачу найти плановую линию развития (тренд) данного явления, характеризующую основную тенденцию её динамики.
Для отображения основной тенденции развития явления применяются полиномы разной степени, при которых оценка параметров производится по МНК. Так, для линейного тренда y=a+bt система уравнений следующая:
 |
Таблица 7. Расчет параметров линейного тренда.
| год | тыс.чел. | t | t2 | уt |
| 1992 | 29,3 | 1 | 1 | 29,3 |
| 1993 | 29,25 | 2 | 4 | 58,5 |
| 1994 | 48,03 | 3 | 9 | 144,09 |
| 1995 | 60,06 | 4 | 16 | 240,24 |
| 1996 | 66,39 | 5 | 25 | 331,95 |
| 1997 | 96,26 | 6 | 36 | 577,56 |
| 1998 | 93,59 | 7 | 49 | 655,13 |
| 1999 | 84,74 | 8 | 64 | 677,92 |
| 2000 | 92,91 | 9 | 81 | 836,19 |
| 2001 | 81,26 | 10 | 100 | 812,6 |
| 2002 | 69,73 | 11 | 121 | 767,03 |
| 2003 | 76,85 | 12 | 144 | 922,2 |
| 2004 | 67,9 | 13 | 169 | 882,7 |
| 2005 | 54,13 | 14 | 196 | 757,82 |
| итого | 950,4 | 105 | 1015 | 7693,23 |
Из таблицы 7 подставим значения в систему и получим:
Уравнение "линейной" модели примет вид: 
 |
 |
 |
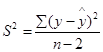Оценим параметры уравнения на типичность. Для расчёта используем следующие формулы:
где: S2 - остаточная уточнённая дисперсия; mа , mв - ошибки по параметрам.
После подстановки значений получились следующие данные:
 |
 |
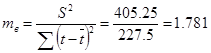
Оценим значимость параметров модели по критерию Стьюдента. Предположим, что параметры и коэффициент корреляции стат. значимы.
 |
где: ta , tb - расчётное значение t-критерия Стьюдента для параметров.
После подстановки данных в формулы получим следующие значения:
Сравним полученное значение с табличным tтабличное при Р=0,05 (уровень значимости) и (n-2)= 2,1788. Так как tрасчётное > tтабличное , то параметры уравнения типичны (значимы) и данное уравнение используется в дальнейших расчетах.
Оценим уравнение в целом по критерию Фишера, выдвигаем гипотезу Н0 : о том, что коэффициент регрессии равен нулю.
Fф=Dфакт /Dост =2410,54/405,25=5,95.
FT (v1 =1;v2 =12)=4,75.
Поскольку Fф > FT при 5%-ном уровне значимости гипотеза Н0 отвергается, уравнение в целом стат. значимо.
Из уравнения видно, что ежегодно численность безработных возрастала в среднем на 2,49%.
Построим график исходных данных.
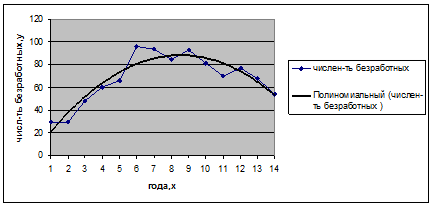
Рис. 2. График исходных данных.
По графику видно, что временной ряд характеризуется сначала тенденцией возрастания до 2000г., а затем убывания. Можно предположить, что данный ряд, вероятно, развивается согласно полиномиальной функции, которая описывается параболой второго порядка: 
Система нормальных уравнений для расчета параметров параболы 2-ой степени составит:
год |
тыс.чел. | t | t2 | t3 | t4 | yt | yt2 |
| 1992 | 29,3 | 1 | 1 | 1 | 1 | 29,3 | 29,3 |
| 1993 | 29,25 | 2 | 4 | 8 | 16 | 58,5 | 117 |
| 1994 | 48,03 | 3 | 9 | 27 | 81 | 144,09 | 432,27 |
| 1995 | 60,06 | 4 | 16 | 64 | 256 | 240,24 | 960,96 |
| 1996 | 66,39 | 5 | 25 | 125 | 625 | 331,95 | 1659,75 |
| 1997 | 96,26 | 6 | 36 | 216 | 1296 | 577,56 | 3465,36 |
| 1998 | 93,59 | 7 | 49 | 343 | 2401 | 655,13 | 4585,91 |
| 1999 | 84,74 | 8 | 64 | 512 | 4096 | 677,92 | 5423,36 |
| 2000 | 92,91 | 9 | 81 | 729 | 6561 | 836,19 | 7525,71 |
| 2001 | 81,26 | 10 | 100 | 1000 | 10000 | 812,6 | 8126 |
| 2002 | 69,73 | 11 | 121 | 1331 | 14641 | 767,03 | 8437,33 |
| 2003 | 76,85 | 12 | 144 | 1728 | 20736 | 922,2 | 11066,4 |
| 2004 | 67,9 | 13 | 169 | 2197 | 28561 | 882,7 | 11475,1 |
| 2005 | 54,13 | 14 | 196 | 2744 | 38416 | 757,82 | 10609,5 |
| итого | 950,4 | 105 | 1015 | 11025 | 127687 | 7693,23 | 73913,9 |
Решив систему, получим параметры уравнения тренда:
а=13,37; b=13,94; c=-1,0017.
Соответственно уравнение тренда составит: у =13,37+13,94t-1,0017t2
|
|
|
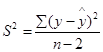Оценим параметры уравнения на типичность.
где: S2 - остаточная уточнённая дисперсия; mа , mв, mr - ошибки по параметрам.
После подстановки значений получились следующие данные:
|
|
|
 |
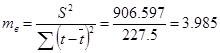
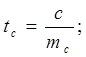Оценим значимость параметров модели по критерию Стьюдента.
Предположим, что параметры и коэффициент корреляции стат.
значимы. Для расчёта использую следующие формулы:
где: ta , tb , tr - расчётное значение t-критерия Стьюдента для параметров.
После подстановки данных в формулы получил следующие значения:
Сравним полученное значение с табличным t-критерием Стьюдента. tтабличное при Р=0,05 и (n-2)= 2,1788. Так как tрасчётное > tтабличное , то параметры b и r уравнения типичны (значимы). Так как tрасчётное < tтабличное , то параметры с и а незначимы.
Оценим уравнение в целом по критерию Фишера, выдвигаем гипотезу Н0 :о том, что коэффициент регрессии равен нулю.
Fф=Dфакт /Dост =10333,6/906,597=11,398.
FT (v1 =1;v2 =12)=4,75.
Т.к. Fф > FT при 5%-ном уровне значимости гипотеза Н0 отвергается, уравнение в целом стат. значимо.
5. Автокорреляция уровней временного ряда.
Для выбора прогностической модели необходимо исследовать автокорреляцию уровней динамического ряда, т.е. изучить корреляционную связь между последовательными значениями уровней временного ряда.
Таблица 9. Расчет коэффициента автокорреляции.
| год | тыс.чел. | yt-1 | yt-2 | yt-3 |
| 1992 | 29,3 | - | - | - |
| 1993 | 29,25 | 29,3 | - | - |
| 1994 | 48,03 | 29,25 | 29,3 | - |
| 1995 | 60,06 | 48,03 | 29,25 | 29,3 |
| 1996 | 66,39 | 60,06 | 48,03 | 29,25 |
| 1997 | 96,26 | 66,39 | 60,06 | 48,03 |
| 1998 | 93,59 | 96,26 | 66,39 | 60,06 |
| 1999 | 84,74 | 93,59 | 96,26 | 66,39 |
| 2000 | 92,91 | 84,74 | 93,59 | 96,26 |
| 2001 | 81,26 | 92,91 | 84,74 | 93,59 |
| 2002 | 69,73 | 81,26 | 92,91 | 84,74 |
| 2003 | 76,85 | 69,73 | 81,26 | 92,91 |
| 2004 | 67,9 | 76,85 | 69,73 | 81,26 |
| 2005 | 54,13 | 67,9 | 76,85 | 69,73 |
| итого | 950,4 | 896,27 | 828,37 | 751,52 |
По данному ряду определяю серию коэффициентов автокорреляции (автокорреляционную функцию):
ra1 =0,809, ra2 =0,52, ra3 =0,233, ra4 =-0,421, ra5 =-0,854, ra6 =-0,746, ra7 =-0,894, ra8 =-0,907, ra9 =-0,735, ra10 =-0,898, ra11 =-0,919.
Построим график автокорреляционной функции.
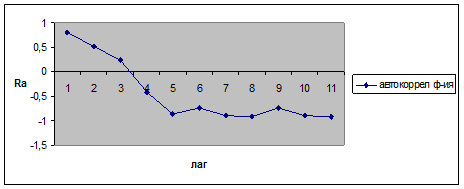
Рис. 3. Коррелограмма для ряда численности безработных в РБ за 1992-2005гг.
Коррелограмма представляет собой затухающую функцию. По графику видно, что наиболее высоким оказался ra 1 =0,809, т.е. уровни текущего года на 80,9% обусловлены уровнями предыдущего года. Поэтому ряд содержит только тенденцию и не содержит периодических колебаний. В данном ряду отсутствует трендовая компонента Т и циклическая (сезонная) компонента S.
3.3. Многофакторный корреляционно – регрессионный анализ безработицы
Таблица 10. Исходные данные.
| год | Уровень безраб-цы | Индекс ВРП | Доход на душу насел-я | Доля пенсионеров |
| 1992 | 5,8 | 77,3 | 51,7 | 18,7 |
| 1993 | 5,9 | 93,3 | 137,4 | 19,6 |
| 1994 | 9,8 | 85,5 | 11,2 | 20,2 |
| 1995 | 12,7 | 86,2 | 83,7 | 20,9 |
| 1996 | 14,9 | 93,5 | 89,6 | 21,5 |
| 1997 | 21,3 | 102,2 | 130,5 | 22,1 |
| 1998 | 22,2 | 94,2 | 72,2 | 22,5 |
| 1999 | 17,3 | 108 | 99,9 | 22,8 |
| 2000 | 19,1 | 104,9 | 111,2 | 22,9 |
| 2001 | 18,4 | 106,4 | 110,2 | 23,2 |
| 2002 | 15,4 | 106,4 | 121,5 | 23,3 |
| 2003 | 16,8 | 106,7 | 104,5 | 23,3 |
| 2004 | 15,3 | 103,7 | 104,4 | 23,5 |
| 2005 | 12 | 104,8 | 111,3 | 23,8 |
| итого | 206,9 | 1373,1 | 1339,3 | 308,3 |
| средн | 14,779 | 98,079 | 95,664 | 22,0214 |
Для корреляционно-регрессионного анализа необходимо из нескольких факторов произвести предварительный отбор факторов для регрессионной модели. Сделаем это по итогам расчета коэффициента корреляции. А именно возьмем те факторы, связь которых с результативным признаком будет выражена в большей степени. Начнем наш анализ с рассмотрения следующих факторов:
- Индекс ВРП - x1 (%)
- Доход на душу населения – x2 (%)
- Доля пенсионеров - x3 (%)
Рассчитаем коэффициент корреляции для линейной связи и для имеющихся факторов - x1 , x2 и x3 . Коэффициент корреляции определяется по следующей формуле:
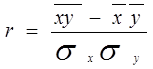
где: 
и 
– дисперсии факторного и результативного признака соответственно; xy – среднее значение суммы произведений значений факторного и результативного признака; xи y – средние значения факторного и результативного признака соответственно.
Для фактора x1 получаем коэффициент корреляции r1 : r1 = 0,627
Для фактора x2 получаем коэффициент корреляции r2 : r2 =0,295
Для фактора x3 получаем коэффициент корреляции r3 : r3 =0,717
По полученным данным можно сделать вывод о том, что:
1)Связь между x1 и y прямая (так как коэффициент корреляции положительный) и умеренно сильная. Поэтому, будем использовать фактор в дальнейших расчётах.
2)Связь между x2 и y прямая (так как коэффициент корреляции положительный) и умеренная, так как она находится между 0,21 и 0,30. Таким образом, возникает необходимость исключить данный фактор из дальнейших исследований.
3)Связь между x3 и y прямая (так как коэффициент корреляции положительный) и сильная. Также будем использовать данный фактор в дальнейших расчетах.
Таким образом, два наиболее влиятельных фактора - индекс ВРП и доля пенсионеров. Для имеющихся факторов x1 и x3 составим уравнение множественной регрессии. Для анализа воспользуемся линейной формой связи, т.е. составим линейное уравнение, т.к. линейное уравнение легче подвергать анализу, интерпретации.
Проверим факторы на мультиколлинеарность, для чего рассчитаем коэффициент корреляции rx 1 x 3 :
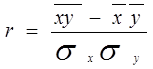
где: и – дисперсии факторного и результативного признака соответственно; x,y – среднее значение суммы произведений значений факторного и результативного признака; xи y – средние значения факторного и результативного признака соответственно.
Подставив имеющиеся данные (из таблицы 10) в формулу, имеем следующее значение: rx 1 x 3 =0,8998.Полученный коэффициент говорит об очень высокой связи, поэтому дальнейший анализ по обоим факторам вестись не может. Однако в учебных целях продолжим анализ.
Проводим оценку существенности связи с помощью коэффициента множественной корреляции:
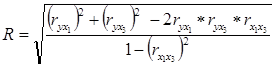
где: ryx 1 – коэффициент корреляции между y и x1 ; ryx 3 – коэффициент корреляции между y и x3 ; rx 1 x 3 – коэффициент корреляции между x1 и x3 .
Подставив имеющиеся данные в формулу и получим: R=0,717
Так как R < 0,8, то связь признаем не существенной, но, тем не менее, в учебных целях, проводим дальнейшее исследование.
 |
Уравнение прямой имеет следующий вид: ŷ = a + bx1 + cx3
Для определения параметров уравнения необходимо решить систему:
Решив систему, получим уравнение: Ŷ=14,72+0,00023 x1 +0,00086x3
Для данного уравнения найдем ошибку аппроксимации:
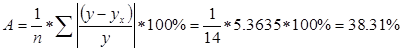
А> 5%, то данную модель нельзя использовать на практике.
Проведем оценку параметров на типичность. Рассчитаем значения величин:
S2 =28,039
ma =1,415; mb =0,023; mс =0,8404;
ta =10,403; tb =0,01; tc =0,001.
Сравним полученные выше значения t для α = 0,05 и числа степеней свободы (n-2)с теоретическим значением t-критерия Стьюдента, который tтеор = 2,1788. Расчетные значения tb и tс < tтеор , значит данные параметры не значимы и данное уравнение не используется для прогнозирования.
Далее оценим существенность совокупного коэффициента множественной корреляции на основе F-критерия Фишера по формуле:
где: n – число уровней ряда; к – число параметров; R – коэффициент множественной корреляции.
После расчета получаем: F=5,819
Сравним Fрасч с Fтеор для числа степеней свободы U1 = 9 и U2 = 2, видим, что 0,045 < 19,40, то есть Fрасч < Fтеор - связь признаётся не существенной, то есть корреляция между факторами x1 , x3 и у не существенна.
3.4. Прогнозирование безработицы
Определив наличие тенденции, можно начать прогнозирование. Прогнозирование проводится следующими методами:
1)на основе средних показателей динамики;
2)на основе экстраполяции тренда;
3)на основе скользящих и экспоненциальных средних.
I. Сначала проведем прогнозирование методом среднего абсолютного прироста. Для этого надо проверить выполняются ли предпосылки. Вычисляем данные для подстановки в формулы предпосылок:
ρ2 = 310,14
σ2 ост = 250,11
т.к. σ2 ост < ρ2 , условие выполняется, значит можно строить прогноз на основе среднего абсолютного прироста. Вычислим средний абсолютный прирост:
, где yp
- прогнозируемый уровень; yb
- конечный уровень ряда как наиболее близкий к прогнозируемому; L-период упреждения; ∆- средний абс.прирост.
Подставляем значения yb =54,13 L=1 ∆=1,91 в функцию прогноза:
yp =54,13+1,91*1=56,04 – прогноз на 2006г.
yp =54,13+1,91*2=57,95 – прогноз на 2007г.
Фактически численность безработных в 2006г. составила 60,6 тыс.чел.
Вычислим ошибку прогноза для сравнения методов прогнозирования на точность: 60,6-56,04=4,56 тыс.чел.
Теперь составим прогноз методом среднего темпа роста. Вычислим средний темп роста: yp = yb *КL
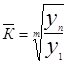=1,0096
Подставим это значение в формулу и составим прогноз на 2006г.:
yp =54,13*1,00961 =54,65
Вычислим ошибку: 60,6-54,65=5,95тыс.чел.
Так как ошибка при прогнозировании методом среднего абсолютного прироста меньше ошибки при прогнозировании методом среднего темпа роста, то можно сделать вывод, что прогнозирование первым методом дает более точные результаты. Поэтому мы оставляем для анализа результатов данные прогноза полученные методом среднего абсолютного прироста. Составим диаграмму при прогнозировании методом абсолютного прироста.
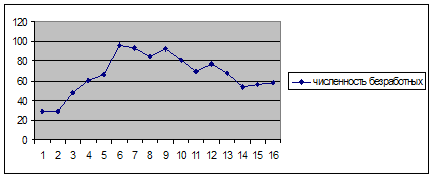
Рис. 4.Численность безработных при прогнозировании «методом абсолютного прироста»
II. Следующий способ прогнозирования - методом экстраполяции тренда.
Ранее по аналитическому выравниванию нашли уравнение параболы второй степени: у =13,37+13,94t-1,0017t2
Сделаем прогноз на 2006г., примем t=7, т.к. нумерация дат определена с середины ряда, т.е. ∑t=0.
уp =13,37+13,94*7-1,0017*49=60,87 – прогноз на 2006г.
Определим доверительный интервал прогноза, в основе которого лежит показатель колеблемости уровней ряда. Колеблемость уровней ряда определяется по формуле: Sy =
Sy =91,44
Интервал определяется с помощью ошибки прогноза Sp = Sy *Q, где Q- поправочный коэффициент, учитывающий период упреждения.
Q= = 1,2127
Тогда ошибка прогноза: Sp =91,44*1,2127=110,886
Соответственно доверительный интервал прогноза составит: уp +t*Sp , где t-табличное значение t-критерия Стьюдента. При ά=0,05 и числе степеней свободы n-3= 11 t=2,2010.
уp +2,2010*110,886 или 61,87 +244,061, т.е. -182,2< уp <305,93
Значит, прогнозная величина находится в данном интервале.
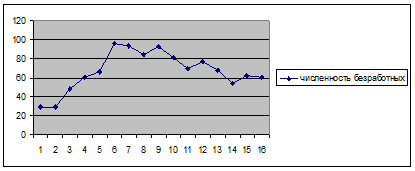
Рис.5. Численность безработных при прогнозировании «методом экстраполяции тренда»
III. Метод скользящих и экспоненциальных средних.
Ранее в своих расчетах я определила, что ряд не содержит периодических колебаний и отсутствуют трендовая компонента Т и циклическая (сезонная) компонента S. Поэтому нет необходимости использовать метод скользящих средних.
Метод экспоненциальных средних.
Экспоненциальное сглаживание является простым методом, который в ряде наблюдений позволяет строить приемлемые прогнозы наблюдаемых временных рядов. Суть метода в том, что исходный ряд x(t) сглаживается с некоторыми экспоненциальными весами, образуется новый временной ряд S(t) (с меньшим уровнем шума), поведение которого можно прогнозировать.
Веса в экспоненциальных средних устанавливаются в виде коэффициентов ά(|ά|<1). В качестве весов используется ряд:
ά; ά(1- ά); ά(1- ά)2 ; ά(1- ά)3 и т.д.
Экспоненциальная средняя определяется по формуле: 
где Qt – экспоненциальная средняя (сглаженное значение уровня ряда) на момент t; ά- вес текущего наблюдения при расчете экспонен. средней; yt –фактический уровень ряда; Qt -1 -экспонен. средняя предыдущего периода.
Каждый новый прогноз основывается на предыдущем прогнозе:
St = St -1 +ά( yt -1 - St -1 ),
где St - прогноз для периода t; St -1 -прогноз предыдущего периода; ά- сглаживающая константа; yt -1 - предыдущий уровень.
Например, St =29,3+0,5*(29,25-29,3)=29,275.
При прогнозе учитывается ошибка предыдущего прогноза, т.е. каждый новый прогноз St получается в результате корректировки предыдущего прогноза с учетом ошибки.
Таблица 12. Расчет прогноза и ошибки.
| 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | |
| yt | 29,3 | 29,25 | 48,03 | 60,06 | 66,39 | 96,26 | 93,59 | 84,74 | 92,91 | 81,26 | 69,73 | 76,85 | 67,9 | 54,13 | - |
| прогноз | - | 29,3 | 29,28 | 38,65 | 49,36 | 57,87 | 77,07 | 85,33 | 85,03 | 88,97 | 85,12 | 77,42 | 77,14 | 72,52 | 60,32 |
| ошибка | - | -0,05 | 18,76 | 21,41 | 17,03 | 38,39 | 16,52 | -0,59 | 7,876 | -7,71 | -15,4 | -0,57 | -9,24 | -18,4 |
10-09-2015, 15:39 Разделы сайта |