МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

МОСКОВСКИЙ ИНЖЕНЕРНО ФИЗИЧЕСКИЙ ИНСТИТУТ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Факультет КИБЕРНЕТИКИ Кафедра «Компьютерные системы и технологии»

РЕФЕРАТ

по курсу:

Архитектура ВС

на тему:

Архитектура квантовых компьютеров.

Студент группы К9-122 Островский А.В.

Москва 2001

Содержание

ВВЕДЕНИЕ

ГЛАВА 1: История появления теории квантовых компьютеров:

1.1 Рождение квантовой физики;

1.2 Появление теории квантовых компьютеров;

1.3 Квантовая физика и квантовая информатика;

ГЛАВА 2: Принципы и понятия, положенные в основу работы

квантовых компьютеров:

2.1 Единицы квантовой информации. Кубит;

2.2 Единицы квантовой информации. Квантовый регистр;

2.3 Квантовая коррекция ошибок в квантовом компьютере;

ГЛАВА 3: Архитектура квантовых копьютеров:

3.1 Принципиальная схема квантового компьютера;

3.2 Общие требования к элементной базе квантового компьютера;

3.3 Основные направления в развитии элементной базы квантовых компьютеров:

3.3.1 Квантовые компьютере на основе ионов, захваченных ионными ловушками;

3.3.2 Квантовые компьютеры на основе молекул органических жидкостей с косвенным скалярным взаимодействием между ними и методов ядерного магнитного резонанса (ЯМР) для управления кубитами;

3.3.3 Квантовые компьютеры на основе зарядовых состояний куперовских пар;

3.3.4 Твердотельные ЯМР квантовые компьютеры;

ГЛАВА 4: Перспективы развития квантовых компьютеров:

4.1 Нерешенные проблемы на пути построения квантовых компьютеров;

4.2 Квантовая связь и криптография;

4.3 Будущее квантовых компьютеров;

ЗАКЛЮЧЕНИЕ

ЛИТЕРАТУРА

ВВЕДЕНИЕ

Элементная база современных информационных систем построена на лампах, транзисторах, лазерах, фотоэлементах, являющихся классическими, в том смысле, что их внешние параметры (токи, напряжение, излучение) являются классическими величинами. С этими величинами связываются информационные символы, что позволяет отображать информационные процессы на физические системы. Аналогично, информационные символы можно связать с дискретными состояниями квантовых систем, подчиняющихся уравнению Шредингера, а с их управляемой извне квантовой эволюцией связать информационный (вычислительный) процесс. Такое отображение превращает квантовую систему (частицу) в квантовый прибор. Совокупность квантовых приборов, используемых для построения квантовых информационных систем, можно назвать квантовой элементной базой.

ГЛАВА 1. История появления теории квантовых компьютеров

1.1 Рождение квантовой физики.

В канун XX века 14 декабря 1900 года немецкий физик и будущий нобелевский лауреат Макс Планк доложил на заседании Берлинского физического общества о фундаментальном открытии квантовых свойств теплового излучения. Этот день считается днем рождения квантовой теории. В физике родилось понятие кванта энергии и среди других фундаментальных постоянных поля вилась постоянная Планка h = 1,38062*10^-23 Дж/К.

В 1925 году В.Гайзенберг предложил матричный вариант квантовой механики, а в 1926 году Э.Шредингер сформулировал свое знаменитое волновое уравнение для описания движения электрона во внешнем поле. В это же время Э.Ферми и П.Дирак получили квантово-статистическое распределение для электронного газа, учитывающее при заполнении отдельных квантовых состояний квантовый принцип, сформулированный тогда же В.Паули. Анализ квантовомеханической задачи о движении электрона во внешнем периодическом поле, создаваемом атомными остатками в кристаллической решетке, выполненный Ф.Блохом в 1928 году, показал, что электронный энергетический спектр в кристаллическом твердом теле имеет зонную структуру . Это привело к существенным изменениям наших представлений о Природе вообще и о твердом теле, в частности.

1.2 Появление теории квантовых компьютеров.

Кардинально новой оказалась идея о квантовых вычисления х, впервые высказанная советским математиком Ю.И.Маниным в 1980 году, и которая стала активно обсуждаться лишь после опубликования в 1982 году статьи американского физика-теоретика нобелевского лауреата Р.Фейнмана. Он обратил внимание на способность изолированной квантовой системы из L двухуровневых квантовых элементов находиться в когерентной суперпозиции из 2^L булевых состояний, характеризующейся 2^L комплексными числами и увеличенной до 2^L размерностью соответствующего гильбертова пространства. Ясно, что для описания такого квантового состояния в классическом вычислительном устройстве потребовалось бы задать 2^L комплексных чисел, то есть, понадобились бы экспоненциально большие вычислительные ресурсы. Отсюда был сделан обратный вывод о том, что эффективное численное моделирование квантовых систем, содержащих до сотни двухуровневых элементов, практически недоступно классическим компьютерам, но может эффективно осуществляться путем выполнения логических операций на квантовых системах, которые действуют на суперпозиции многих квантовых состояний.

Поскольку законы квантовой физики на микроскопическом уровне являются линейными и обратимыми, то и соответствующие квантовые логические устройства оказываются также логически и термодинамически обратимыми , а квантовые вычислительные операции представляются унитарными операторами (или матрицами 2^L ╠ 2^L ) в 2^L -мерном гильбертовом пространстве. Квантовые вентили аналогичны соответствующим обратимым классическим вентилям, но в отличие от классических они способны совершать унитарные операции над суперпозициями состояний . Выполнение унитарных логических операций предполагается осуществлять с помощью соответствующих внешних воздействий, которыми управляют классические компьютеры.

1.3 Квантовая физика и квантовая информатика

Возможность построения квантовых компьютеров и систем связи подтверждается современными теоретическими и экспериментальными исследованиями. Новая техника XXI в. рождается путем синтеза новых идей в математике, физике, информатике, технологии. Взаимодействие фундаментальных отраслей науки и технологии, рождающее новую технику, показано в таблице 3. Важно подчеркнуть, что в процессе решения задач квантовой информатики происходит развитие и углубление понимания основ квантовой физики, подвергаются новому анализу и экспериментальной проверке основные ее проблемы - локальности (причинности), скрытых параметров, реальности, неопределенности, дополнительности, измерений, коллапса волновой функции.

ГЛАВА 2: Принципы, положенные в основу работы квантовых компьютеров

2.1 Единицы квантовой информации. Кубит.

Любая классическая двухуровневая система, как и квантовая, имеет основное |0ñ и не основное |1ñ базисные состояния. Примером классической двухуровневой системы является известный в микроэлектронике инвертор, осуществляющий операцию НЕ. В зависимости от того заняты ли эти состояния с вероятностями P (0) = 1, P (1) = 0 или P (0) = 0, P (1) = 1, мы имеем булевые логические состояния "0" или "1".

В квантовом случае возникает намного более богатая ситуация. Волновая функция квантовых состояний двухуровневой системы - квантового бита, получившего в дальнейшем название кубита (quantum bit или qubit), может представлять собой суперпозицию базисных состояний (вектор состояния) следующего вида |yñ = a|0ñ + b|1ñ, где a,b - комплексные амплитуды состояний, при этом |a|² + |b|² = 1. Помимо вероятностей P (0) = |a|² и P (1) = |b|² , заполнения базисных состояний |0ñ и |1ñ, состояние кубита характеризуется когерентными или интерференционными слагаемыми в вероятности состояния |yñ, определяемых произведениями комплексных амплитуд ab^* и a^* b. Состояние квантового бита в отличие от классического может изменяться не только путем изменения вероятностей P (0) и P (1), но и более тонко путем изменения амплитуд состояний a и b, что соответствует поворотам вектора состояния |yñ в так называемом гильбертовом двухмерном пространстве состояний. В этом и состоит принципиальное различие классического и квантового бита.

Двум значениям кубита могут соответствовать, например, основное и возбужденное состояния атома, направления вверх и вниз спина атомного ядра, направление тока в сверхпроводящем кольце, два возможных положения электрона в полупроводнике, различающихся поляризацией фотона или фазой сверхпроводника. Квантовая система может быть макроскопической (сверхпроводники, сверхтекучие жидкости, бозе-газ), отдельной атомной частицей или колебательной модой:

Простейшим случаем двухуровневой квантовой системы является спин ядра атома или электрона I = ½ в постоянном внешнем поле B ₀ : два уровня энергии и состояния соответствуют проекциям спина на направление B ₀ (рис. 1).

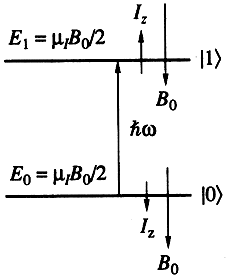
Рис. 1. Состояния спина I _z = ±½ - и его уровни энергии E _0,1 = ± m _i B ₀ /2
во внешнем поле B ₀ представляют логические состояния кубита |0> и |1>

Два оптических уровня энергии и состояния электрона в ионе также могут быть выбраны в качестве двух состояний кубита (рис. 2).

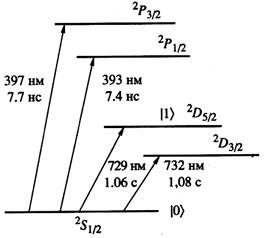
Рис. 2 . Состояния иона Са ⁺ , соответствующие уровням энергии ² S _1/2 (основной) и ² D _5/2 (метастабильный) выбраны за логические |0> и |1> . Числа у стрелок показывают длину волны лазера, вызывающего переход, и время жизни иона на соответствующем уровне

2.2 Единицы квантовой информации. Квантовый регистр.

Квантовый регистр устроен почти так же, как и классический. Это цепочка квантовых битов, над которыми можно проводить одно- и двухбитовые логические операции (подобно применению операций НЕ, 2И-НЕ и т.п. в классическом регистре).

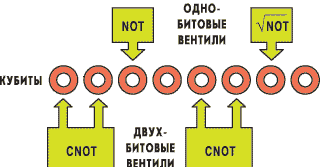Рис. 3 . Квантовый регистр - цепочка квантовых битов. Одно- или двухкубитовые квантовые вентили (NOT ^1/2 , NOT, CNOT и др.) осуществляют логические операции над кубитами или парами кубитов.

К базовым состояниям квантового регистра, образованного L кубитами, относятся, так же как и в классическом, все возможные последовательности нулей и единиц длиной L. Всего может быть 2^L различных комбинаций. Их можно считать записью чисел в двоичной форме от 0 до 2^L -1 и обозначать 0,1,2,3, ... 2^L -1. Однако эти базовые состояния не исчерпывают всех возможных значений квантового регистра (в отличие от классического), поскольку существуют еще и состояния суперпозиции, задаваемые комплексными амплитудами, связанными условием нормировки. Классического аналога у большинства возможных значений квантового регистра (за исключением базовых) просто не существует. Состояния классического регистра - лишь жалкая тень всего богатства состояний квантового компьютера.

Представим, что на регистр осуществляется внешнее воздействие, например, в часть пространства поданы электрические импульсы или направлены лазерные лучи. Если это классический регистр, импульс, который можно рассматривать как вычислительную операцию, изменит L переменных. Если же это квантовый регистр, то тот же импульс может одновременно преобразовать до 2^L переменных. Таким образом, квантовый регистр, в принципе, способен обрабатывать информацию в 2^L / L раз быстрее по сравнению со своим классическим аналогом. Отсюда сразу видно, что маленькие квантовые регистры (L<20) могут служить лишь для демонстрации отдельных узлов и принципов работы квантового компьютера, но не принесут большой практической пользы, так как не сумеют обогнать современные ЭВМ, а стоить будут заведомо дороже. В действительности квантовое ускорение обычно значительно меньше, чем приведенная грубая оценка сверху (это связано со сложностью получения большого количества амплитуд и считывания результата), поэтому практически полезный квантовый компьютер должен содержать тысячи кубитов. Но, с другой стороны, понятно, что для достижения действительного ускорения вычислений нет необходимости собирать миллионы квантовых битов. Компьютер с памятью, измеряемой всего лишь в килокубитах, будет в некоторых задачах несоизмеримо быстрее, чем классический суперкомпьютер с терабайтами памяти.

2.3 Квантовая коррекция ошибок в квантовом компьютере

В самом начале развития идей о квантовом компьютере физики обнаружили и грозного противника этой машины. Имя этого противника –декогерентизация . Кубиты компьютера нельзя полностью изолировать от внешнего мира: кубиты работают в условиях шумового воздействия внешней среды. Флуктуации напряжений на электродах, шумовые токи, неточности выполнения самих импульсных воздействий на кубиты в ходе вычислительного процесса - все это вносит неконтролируемые ошибки в фазы и амплитуды состояний кубитов в ходе вычислительного процесса. По истечении времени, равном времени декогерентизации квантовых состояний системы кубитов, контролируемый вычислительный процесс прекратится, эволюция квантового компьютера приобретет случайный (диффузионный) характер. Время декогерентизации, как правило, будет меньше времени, необходимого для выполнения сложного алгоритма, состоящего из большого числа (-10⁹ ) вентилей.

Выход из этой, казавшейся тупиковой, ситуации был найден в применении методов квантовой коррекции ошибок. Методы коррекции ошибок хорошо известны из теории обычных (классических) компьютеров. Смысл их в том, что логические |0> и |1> кодируются большим числом битов; анализ кодовых комбинаций позволяет найти и удалить ошибку. Эти методы удалось разработать в квантовом варианте, где ошибки могут быть фазовыми и амплитудными. Выяснилось, что если вероятность ошибки при выполнении одной элементарной операции ниже некоторого порогового уровня, вычислительный процесс можно длить сколь угодно долго. Это означает, что операции квантовой коррекции ошибок удаляют из компьютера больше ошибок, чем вносят. Этот вывод очень важен: по существу, он имеет силу теоремы существования полномасштабного квантового компьютера.

ГЛАВА 3: Архитектура квантовых компьютеров

3.1 Принципиальная схема квантового компьютера

Квантовые методы выполнения вычислительных операций, а также передачи и обработки информации, уже начинают воплощаться в реально функционирующих экспериментальных устройствах, что стимулирует усилия по реализации квантовых компьютеров. Квантовый компьютер состоит из n кубитов и позволяет проводить одно- и двухкубитовые операции над любым из них (или любой парой). Эти операции выполняются под воздействием импульсов внешнего поля, управляемого классическим компьютером.

Принципиальная схема работы любого квантового компьютера может быть представлена следующим образом (рис.4). Основной его частью является квантовый регистр - совокупность некоторого числа L кубитов. До ввода информации в компьютер все кубиты регистра должны быть приведены в основные базисные (булевые) состояния. Эта операция называется подготовкой начального состояния или инициализацией (initializing). Далее каждый кубит подвергается селективному воздействию, например, с помощью импульсов внешнего электромагнитного поля, управляемых классическим компьютером, которое переведет основные базисные состояния определенных кубитов в не основное состояния |0ñÞ |1ñ. При этом состояние всего регистра перейдет в суперпозицию базисных состояний вида |n ñ = |n ₁ ,n ₂ ,n ₃ ,...n _L ñ, где n _i = 0,1.

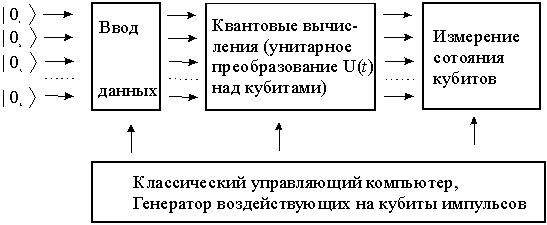
(Рис. 4) – схематическая структура квантового компьютера

При вводе информации в квантовый компьютер состояние входного регистра, с помощью соответствующих импульсных воздействий преобразуется в соответствующую когерентную суперпозицию базисных ортогональных состояний. В таком виде информация далее подвергается воздействию квантового процессора, выполняющего последовательность квантовых логических операций, определяемую унитарным преобразованием, действующим на состояние всего регистра. К моменту времени t в результате преобразований исходное квантовое состояние становится новой суперпозицией, которая и определяет результат преобразования информации на выходе компьютера.

Совокупность всех возможных операций на входе данного компьютера, формирующих исходные состояния, а также осуществляющих унитарные локальные преобразования, соответствующие алгоритму вычисления, способы подавления потери когерентности - так называемой декогерентизации (decoherence) квантовых состояний и исправления случайных ошибок, играют здесь ту же роль, что и "программно е обеспечение" (software) в классическом компьютере.

3.2 Общие требования к элементной базе квантового компьютера

При выборе конкретной схемы любого квантового компьютера необходимо решить три вопроса: во-первых, выбрать физическую систему, представляющую требуемую систему кубитов, во вторых, определить физический механизм, определяющий взаимодействие между кубитами, необходимое для выполнения двухкубитовых операций, в третьих, определить способы селективного управления кубитами и измерения их состояния на выходе. Все это вместе взятое аналогично "аппаратному обеспечению" (hardware) классического компьютера.

Считается, что для реализации полномасштабного квантового компьютера, превосходящего по производительности любой классический компьютер, на каких бы физических принципах он не работал, следует обеспечить выполнение следующих пяти основных требований :

1. Физическая система, представляющая полномасштабный квантовый компьютер, должна содержать достаточно большое число L > 10³ хорошо различаемых кубитов для выполнения соответствующих квантовых операций.

2. Необходимо обеспечить условия для приготовления входного регистра в исходном основном базисном состоянии |0₁ ,0₂ ,0₃ ,...0_L ñ, то есть возможность процесса инициализации .

3. Необходимо обеспечить максимальное подавление эффектов декогерентизации квантовых состояний, обусловленное взаимодействием системы кубитов с окружающей средой, что приводит к разрушению суперпозиций квантовых состояний и может сделать невозможной выполнение квантовых алгоритмов. Время декогерентизации должно, по крайней мере, в 10⁴ раз превышать время выполнения основных квантовых операций (времени такта). Для этого система кубитов должна быть достаточно слабо связана с окружением.

4. Необходимо обеспечить за время такта выполнение требуемой совокупности квантовых логических операций, определяющей унитарное преобразование. Эта совокупность должна содержать определенный набор только двухкубитовых операций, типа контролируемый инвертор или контролируемое НЕ (Controlled NOT º CNOT) (аналог исключающего ИЛИ в классических компьютерах), осуществляющих операции поворота вектора состояния двух взаимодействующих кубитов в четырехмерном гильбертовом пространстве, и однокубитовых операций, осуществляющих поворот вектора состояния кубита в двухмерном гильбертовом пространстве, таких как операции НЕ, Адамара и некоторые другие.

5. Необходимо обеспечить с достаточно высокой надежностью измерение состояния квантовой системы на выходе. Проблема измерения конечного квантового состояния является одной из основных проблем квантовых вычислений.

3.3 Основные направления в развитии элементной базы квантовых компьютеров

3.3.1 Квантовые компьютере на основе ионов, захваченных ионными ловушками

Взаимодействие между заряженными ионами в одномерной цепочке этих ловушек осуществляется посредством возбуждения их коллективного движения, а индивидуальное управление ими с помощью лазеров инфракрасного диапазона. Первый прототип квантового компьютера на этих принципах был предложен австрийскими физиками И.Цираком и П.Цоллером в 1995 году. В настоящее время интенсивные экспериментальные работы ведутся в Los Alamos Natl.Lab. (LANL) и Natl.Inst.Stand.Tech. (NIST) в США. Преимущество такого подхода состоит в сравнительно простом индивидуальном управлении отдельными кубитами. Основными недостатками этого типа квантовых компьютеров являются необходимость создания сверхнизких температур, обеспечение устойчивости состояний ионов в цепочке и ограниченность возможного числа кубитов значением L < 40.

3.3.2 Квантовые компьютеры на основе молекул органических жидкостей с косвенным скалярным взаимодействием между ними и методов ядерного магнитного резонанса (ЯМР) для управления кубитами:

В предложенном способе построения квантового компьютера кубитами выступают спины - ядер водорода (протоны) и углерода ¹³ С в молекулах жидкости. Так, в молекуле трихлорэтилена (рис. 5) спины ядер двух атомов ¹³ С и одного протона образуют три кубита. Два атома ¹³ С химически неэквивалентны и поэтому имеют различные частоты ядерного магнитного резонанса w _A и w _B в заданном внешнем постоянном магнитном поле B ₀ , протон будет иметь третью резонансную частоту w _C . Подавая импульсы внешнего переменного магнитного поля на частотах (ид, tog, о)с, мы селективно управляем квантовой эволюцией любого из этих спинов (выполняем однокубитовые вентили). Между спинами ядер, разделенных одной химической связью ¹ H-¹³ С и ¹³ С-¹³ С, имеется магнитное контактное взаимодействие, что позволяет построить двухкубитовые вентили.

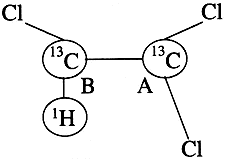Рис. 5. – схема ансамблевого ядерно магнитнорезонансного квантового компьютера

Главным преимуществом такого компьютера является то, что огромное число практически независимых молекул-компьютеров жидкости действует, обеспечивая тем самым возможность управления ими с помощью хорошо известных в технике ядерного магнитного резонанса


29-04-2015, 04:00