Закрытие трещин и его влияние на циклическую трещиностойкость

Государственный комитет Российской Федерации

по высшему образованию

Российский Государственный Авиационный Технологический

Университет имени К.Э. Циолковского - (МАТИ)

_______________________________________________________

Курсовая работа по физическому материаловедению

Тема: Закрытие трещин и его влияние на циклическую

трещиностойкость сплавов

Преподаватель: Ботвина Л.Р.

Студент: Шапиро Р.А.

Москва 1998г

Структурный план курсовой работы

по физическомуматериаловедению.

1. Проявления и механизм закрытия усталостных

трещин.

2. Влияние условий эксплуатации на закрытие и

кинетику трещин усталости в конструкционных

материалах.

3. Закрытие трещин и структура конструкционных

сплавов.

1. Проявления и механизм закрытия усталостных трещин.

Один из наиболее важных феноменов экспериментальной механики усталостного разрушения, установленных в течение 1970-х г., - явление преждевременного контакта берегов растущей усталостной трещины на протяжении некоторой положительной части цикла напряжений. Этот феномен, называемый “смыкание” или “закрытие трещин”, широко используется для объяснения многочисленных кинетических эффектов, сопровождающих усталостное разрушение конструкционных материалов.

Считается, что закрытие трещин обнаружил В. Элбер. По-видимому, правильно сказать, что этот исследователь впервые обнаружил количественную оценку закрытия трещины и указал на его значимость в кинематике усталостного разрушения. Наиболее правдоподобным механизм их образования, предложенный в свое время С. Бичемом, предусматривает взаимное столкновение поверхностей трещины позади ее вершины.

В. Элбер обнаружил закрытие трещин случайно при подготовке образцов для фрактографического исследования. Разрезание образца с усталостной трещиной вызвало его существенную деформацию, заметную невооруженным глазом. Для установления причин такого поведения образца его снабдили датчиком деформации, что позволило получить зависимость приложенной к образцу нагрузки от перемещения краев разреза. Она оказалась нелинейной, хотя нагружение образца осуществлялось в упругой области. Это свидетельствовало о изменении геометрии образца в процессе нагружения. Такое изменение возможно, если в ненагруженном состоянии трещина была закрыта, т.е. ее берега прижаты друг к другу с определенным усилием. Тогда процесс нагружения будет сопровождаться не только равномерной деформацией материала неразрушенной части образца, но и увеличением длины раскрытой части усталостной трещины, т.е. податливость образца будет меняться при изменении приложенного к нему усилия. Путем последовательной регистрации в цикле раскрытия трещины вблизи ее вершины установлено, что усталостные трещины в листах алюминиевого сплава закрываются еще до полного снятия с образца растягивающей нагрузки. В полуцикле нагружения раскрытие берегов трещины вначале не зависит от приложенного извне напряжения (рис. 1, а) и лишь при достижении последним определенного значения трещина начинает открываться, инициируя таким образом процесс деформирования и усталостного повреждения материала в зоне предразрушения. Используя терминологию механики разрушения, можно сказать, что закрытие трещины фиксирует в ее вершине некоторое значение коэффициента интенсивности напряжения К=Кор (пропорциональное текущей длине трещины и нормальному напряжению в момент открытия трещины ор), препятствуя снижению этого параметра до уровня К=Кmin. В результате искажается характер формы цикла и величина трещины (рис. 1, б), а также коэффициент интенсивности напряжения в вершине трещины (рис. 1, в). На основании полученных результатов В. Элбер пришел к выводу о неэффективности с точки зрения роста усталостной трещины некоторой части цикла напряжений. Указывая на необходимость учета явления закрытия трещины при анализе напряженно-деформационного состояния тел с трещинами, он уточнил зависимость скорости роста усталостной трещины от размаха коэффициента интенсивности напряжения, введя эффективное значение последнего параметра: ,

где С и n - коэффициенты Пэриса; - эффективный размах коэффициента интенсивности напряжения, соответствующий открытой трещине

Kmax - Kор

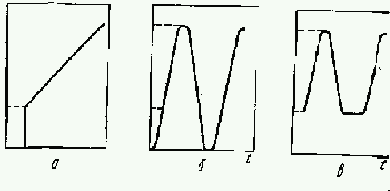
Рис. 1. Зависимость между приложенным к образцу напряжением и раскрытием берегов трещины (а), а также схема формы цикла внешней нагрузки (б) и коэффициента интенсивности напряжения (в).

В зависимости от конкретных условий реализации закрытия трещины связывают с несколькими механизмами. Первый из них предложен В.Элбером, который заметил отличие реальной усталостной трещины от идеальной, т.е. острого надреза нулевой ширины надр. Оно заключается в наличии на берегах реальной усталостной трещины пластически деформируемого материала (рис. 2). Поэтому при однократном нагружении до одинаковых значений коэффициента интенсивности напряжения раскрытие берегов реальной усталостной трещины тр (рис. 2, а) меньше, чем идеальной (рис. 2, б). Если предположить, что в полуцикле разгрузки раскрытия реальной и идеальной трещин будет уменьшаться в равной степени, то берега усталостной трещины сомкнуться раньше полного снятия нагрузки. Поэтому, согласно В. Элберу, усталостная трещина закрывается при положительном значении приложенного извне напряжения благодаря наличию на ее берегах определенного объема пластически деформированного материала, увеличенного по сравнению с исходным недеформируемым, и воздействия на этот объем неразрушенной части сечения.

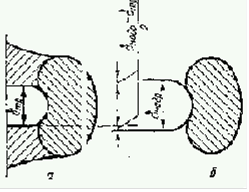
Рис. 2. Конфигурация пластичной зоны в реальной (а) и идеальной (б) усталостных трещинах.

Описанный механизм закрытия, именуемый закрытие трещин обусловленное пластичностью ( ЗТП ), характерен для вязких материалов, нагружаемых в условиях плоского напряженного состояния. Однако с концепцией ЗТП не согласуется многократно подтвержденный экспериментами факт усиления закрытия усталостной трещины по мере снижения размаха коэффициента интенсивности напряжения и перехода к росту усталостной трещины в условиях плоского деформированного состояния. Противоречия между модельными представлениями о процессе закрытия трещин и результатами испытаний позднее были устранены благодаря открытию двух дополнительных механизмов закрытия трещины, характерных для припорогового роста усталостной трещины. Один из них учитывает роль окисления берегов трещины и классифицируется как закрытие трещины обусловленное оксидообразованием ( ЗТО ). Наличие в областях изломов, соответствующих припороговой скорости роста усталостной трещины, хорошо различимых визуально продуктов коррозии. Кроме того, было зафиксировано замедление припорогового роста усталостной трещины в коррозиционой среде по сравнению с воздухом. На основании проведенных на воздухе и в дистиллированной воде исследований роста усталостной трещины в стали, пришли к выводу о том, что образующиеся вблизи вершины трещины продукты окисления могут оказывать расклинивающее влияние аналогично остаточной деформации и тем самым снижать эффективный размах коэффициента интенсивности напряжения в вершине трещины, а также скорость ее роста.

На основании простой модели жесткого клина постоянной толщины а, находящегося внутри трещины длиной l на расстоянии 2с позади ее вершины (рис. 3), сделана попытка аналитической оценки роли коррозионных отложений в усилении закрытия трещины. На основании упругой модели с использованием сингулярных интегральных уравнений или функции напряжений Вестергаарда получено выражение для коэффициента интенсивности напряжения в вершине трещины с клином, учитывающее только механическое расклинивание трещины и игнорирующее пластичность материала и шероховатость поверхностей излома:

Kr |=0=, ()

где Е’=Е - для плоского напряженного состояния; Е’= - для условий

плоской деформации; Е - модуль упругости материала; - коэффициент Пуассона.

Поскольку при K=Kr трещина будет закрытой, можно принять параметр Kr равным значениюкоэффициенту интенсивности напряжения в момент закрытия трещины, соответственно:Kmax - Kr

Все приведенные соображения имеют смысл при условии, что минимальное раскрытие трещины меньше, чем толщина оксидов, т.е. Kmin < Kr. На основании уравнения () построены (рис. 4) графические зависимости коэффициента интенсивности напряжения Kr от толщины клина (а=10нм-10мм) и от его удаления от вершины (с= 10нм-100мм).

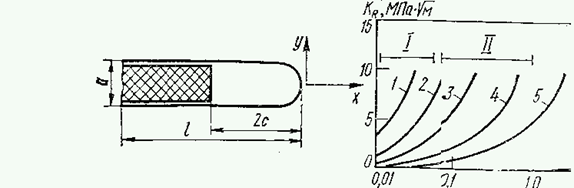
Рис. 3. Расчетная модель жесткого клина для оценки закрытия трещины.

Рис. 4. Зависимости коэффициента интенсивности напряжения Kr в момент контакта берегов трещины от толщины клина а и его удаления от вершины трещины 2с:

1 - с=10нм; 2 - с=0.1мкм; 3 - с=1мкм; 4 - с=10мкм; 5 - с=100мкм; I - толщина естественного окисления;

II - толщина фреттинг-окисления.

Иной вид закрытия, который аналогично рассматриваемому выше ЗТО наиболее характерен для припороговой усталости при пульсирующем и близких к нем циклах напряжений, - закрытие трещин, обусловленное шероховатостью поверхностей разрушения ( ЗТШ ). Считают, что когда высота неровностей рельефа излома соизмерима с величиной раскрытия вершины трещины, а в напряженное состояние материала зоны предразрушения вносит существенный вклад сдвиговая компонента, уровень закрытия может существенно увеличиться путем раслинивания трещины в отдельных контактирующих точках вдоль ее траектории.

Существенно усиление закрытие трещины, связанного с шероховатостью вблизи пороговых размахов коэффициента интенсивности напряжения, объясняют следующим образом. Для припорогового роста усталостной трещины, как правило, реализуются условия

ry < d , ()

где ry - радиус пластической зоны у вершины трещины; d - размер зерна или другого структурного элемента контролирующего процесс разрушения.

Согласно представлениям, развитым Б. Томкинсом, для низких размахов коэффициента интенсивности напряжения , когда выполняется условие (), распространение трещины через зерно будет проходить вдоль определенной кристаллографической плоскости. При переходе в другое зерно ввиду произвольной ориентации последнего по отношению к первому ориентация трещины изменяется. Это обеспечивает фасеточный характер излома (рис. 5). Такой сложный кристаллографический характер распространения трещины с ее значительными отклонениями от линии нормального отрыва обусловливает наличие существенной сдвиговой компоненты усилий и деформацию продольным сдвигом. В итоге сдвига сопряженных поверхностей излома и нарушения соответствия между элементами рельефа “впадина-выступ” ЗТШ усиливается. Этот вид закрытия трещины существенно влияет на кинематику роста усталостной трещины и размах порогового коэффициента интенсивности напряжения, поскольку циклическое раскрытие вершины трещины невелико и соизмеримо с шероховатостью поверхностей излома.

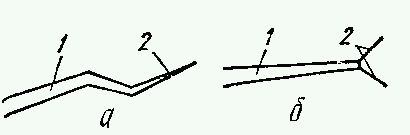
Рис. 5. Схема траектории (1) и распространение полос скольжения (2) в вершине трещины, растущей с припороговой скоростью (а) и скоростью, соответствующей среднеамплитудному участку кинематической диаграмме усталостного разрушения (б).

Первая попытка количественной оценки влияния шероховатости поверхности разрушения на закрытие усталостной трещины сделана на основании сопоставления высоты микронеровностей в изломе и раскрытия вершины трещины. Однако оценка роста усталостной трещины по такой упрощенной модели приводили к значительному занижению результатов, поскольку не учитывается роль сдвиговой деформации в вершине трещины. Указанный недостаток устранен в позднее предложенной геометрической модели ЗТШ (рис. 6), согласно которой величина эффекта закрытия записывается в виде

,

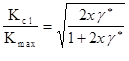где - безразмерный коэффициент шероховатости поверхности разрушения; x= .

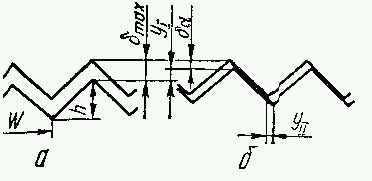
Рис. 6. Схема распространения сопряженных берегов трещины при значениях К=Кmax (a) и К=Кcl (б). Здесь max - раскрытие трещины при Кmax ;cl - раскрытие трещины приКcl

Недостатками рассмотренной модели является ее двухмерность, из-за которой деформационное поведение поверхностных и внутренних (по толщине) слоев образца не может быть идентичным. Поэтому двухмерная модель ЗТШ дает лишь какое-то усредненное вдоль фронта трещины описание процесса закрытия трещины. Еще более существенный недостаток рассматриваемого подхода- полное игнорирование других механизмов закрытия трещины. Впрочем, это относится также и к описанным выше модели жесткого клина, концентрирующие внимание исключительно на ЗТО, а так же ко всем остальным попыткам аналитического описания сложного по физической природе и многообразию реализующегося явления закрытия трещин.

Существуют еще два механизма закрытия усталостных трещин, которые реже реализуются на практике, чем описанные выше: закрытие, обусловленное вязкостью рабочей среды, и закрытие, обусловленное объемными изменениями, сопровождающими фазовые превращения материала зоны разрушения. Наличие в трещине вязкой среды препятствует перемещению ее берегов как в полуцикле нагружения, так и при его разгрузке. Поэтому рост усталостной трещины чувствителен к вязкости инертных жидких сред и частоте нагружения. В коррозионной жидкой среде возможно дополнительное повышение ее вязкости во времени за счет растворения образующихся на берегах трещины продуктов коррозии. В этом случае влияние вязкости неоднозначно, ее повышение усиливает потенциальную возможность жидкости создавать внутреннее давление в трещине, хотя и ограничивает проникающую способность. Ситуация, возникающая при росте усталостной трещины в присутствии вязкой среды, может быть смоделирована с учетом раскрытия трещины, плотности и кинематической вязкости жидкости, а также поверхностного натяжения и угла смачивания. Полученные расчетным путем результаты свидетельствуют, что для широкого диапазона вязкостей максимальное значение напряжений, обусловленных внутренним давлением жидкости, не превышают среднего значения цикла приложенных извне напряжений. Поэтому рассматриваемый механизм закрытия трещины влияет на кинематику роста усталостной трещины в меньшей степени, чем ЗТП, ЗТО или ЗТШ.

В некоторых случаях закрытие трещины может усиливаться за счет увеличения объема материала в зоне предразрушения вследствие локальных фазовых превращений, вызываемых механическими напряжениями. Этот механизм закрытия трещины во многом аналогичен ЗТП, отличаясь, однако, физической природой процесса образования “лишнего” материала и полости распространяющейся трещины.

Таким образом, различаются пять механизмов закрытия трещины усталости (рис. 7). В силу специфической природы реализация двух последних (рис. 7, а, б) возможна лишь в особых условиях: при наличии жидкой среды в вершине трещины или при усталостном разрушении сложнолегированных металлических сплавов, содержащих метастабильные структурные составляющие. В то же время ЗТП, ЗТО и ЗТШ (рис. 7, в-д) более универсальны.

Рис. 7. Схемы механизмов закрытия трещины, обусловленных вязкостью рабочей среда (а), фазовыми превращениями в зоне предразрушения (б), ЗТП (в), ЗТО (г) и ЗТШ (д).

2. Влияние условий эксплуатации на закрытие и кинетику

трещин усталости в конструкционных материалах.

Уровень закрытия трещины определяется рядом факторов, которые условно делятся на две группы - эксплуатационные и структурные. К первой относятся параметры цикла напряжений (размах, асимметрия, частота), окружающая среда (ее химическая активность, влажность, температура), а также характер напряженно- деформированного состояния у вершины трещины в образце или элементе конструкции, который определяется их геометрией и размерами. Основные структурные факторы (вторая группа) обусловлены химическим составом материала и его микроструктурным состоянием.

Зависимость закрытия трещины от уровня размаха коэффициента интенсивности напряжения. Закрытие трещины характерно для припорогового роста усталостной трещины, оно монотонно ослабевает по мере роста размаха коэффициента интенсивности напряжения . Это объясняется увеличением по мере роста коэффициента интенсивности напряжения раскрытия трещин, величина которого в конечном итоге исключает появление закрытия трещины. Максимальный коэффициент интенсивности напряжения Kmax, при котором не происходит закрытие трещины, зависит от ряда факторов, в том числе от структуры сплава и эксплуатационных условий, включая асимметрию цикла.

Связь закрытия трещины с асимметрией цикла. Влияние асимметрии цикла на проявление закрытия трещины исследовано весьма широко. Повышение коэффициента асимметрии в сторону положительных значений вызывает снижение закрытие трещины и увеличение скорости роста усталостной трещины. По мере снижения размаха коэффициента интенсивности напряжения и скорости рост усталостной трещины чувствительность закрытия к асимметрии цикла напряжений усиливается до максимального уровня на пороге усталости. Ослабление роли закрытия трещины по мере роста коэффициента асимметрии объяснят тем, что повышении коэффициента асимметрии происходит сближение значений минимального коэффициента интенсивности напряжения Kmin и коэффициента интенсивности напряжения, характеризующего момент открытия трещины Kор. Поэтому при более высоких коэффициентах асимметрии уменьшается размах коэффициента интенсивности напряжения, соответствующий закрытой трещине = Kop - Kmin и, следовательно, возрастает эффективный размах (рис. 8, а). Такие соображения приводят к зависимостям пороговых характеристик ( рис. 8, б), и хорошо согласуются с результатами опытов.

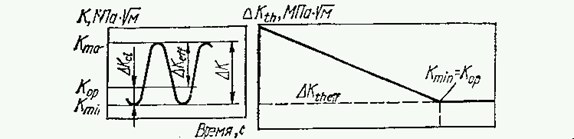
Рис. 8. Параметры цикла нагружения (а) и зависимости пороговых размаха коэффициента интенсивности напряжения (б).

Частота нагружения. На воздухе частотные зависимости пороговой интенсивности напряжений различных материалов неоднозначны. Если в титановом сплаве Ti-6Al-6V-2Sn повышение частоты цикла снижает пороговый размах коэффициента интенсивности напряжения, то в алюминиевом сплаве эффект обратный. При этом линейная зависимость параметраот частоты сохраняется для всех исследуемых форм циклов напряжений. Увеличение частоты нагружения значительно интенсифицирует автокаталитическое окисидообразавание на поверхности разрушения, о чем свидетельствует и различный характер зависимостей скорости роста усталостной трещины при постоянном размахе коэффициента интенсивности напряжения от ее длины, а также вид поверхностей разрушения.

Влияние повышенной температуры испытаний. Данные о влиянии температуры испытаний на кинематику роста усталостной трещины в припороговой области весьма противоречивы. Например, сопротивление припороговому росту усталостной трещины нержавеющей стали повышается с увеличением температуры от 290 до 970К при испытаниях на воздухе, однако остается постоянным в вакууме и гелии. Для корпусных перлитных сталей зависимость порогового размаха коэффициента интенсивности напряжения от температуры испытаний немонотонна - снижение порогового размахакоэффициента интенсивности напряжения при повышении температуры до 420-470К сменяется его ростом при более высоких температурах. Характерной особенностью роста усталостной трещины при повышенных температурах является независимость порогового размаха коэффициента интенсивности напряжения от температуры испытаний в условиях нагружения с высокой асимметрией цикла напряжений.

Для понимания причины, определяющих особенности припороговой кинетики роста усталостной трещины в конструкционных сталях при


29-04-2015, 04:02