3.4. Расчёт промежутков внешней изоляции,

подвергаемых воздействию грозовых импульсов

При полных грозовых импульсах положительной (+) и отрицательной (-) полярности полного импульса 1,5/40 мксек минимальная длина изоляционного промежутка l^*, см определяется по U_{расч.гр}, кВ.

При импульсах положительной (+) полярности {5, стр.124, рис.3-15}

- Для промежутка l₂ минимальная длина составляет:

U_{расч.гр} = (1,05  1,1)^.U_имп/n = (1,05  1,1)^.1600/4 = 420  440 кВ,

l₂^* = 65,0  70,0 см;

- Для промежутка l₃ минимальная длина составляет:

U_{расч.гр} = (1,05  1,1)^.U_имп/n = (1,05  1,1)^.1600/10 = 168  176 кВ,

l₃^* = 19,0  21,0 см;

- Для промежутка l₄ минимальная длина составляет:

U_{расч.гр} = (1,05  1,1)^.U_имп/n = (1,05  1,1)^.1600/8 = 210  220 кВ,

l₄^* = 65,0  70,0 см;

При импульсах отрицательной (-) полярности

- Для промежутка l₂ минимальная длина составляет:

U_{расч.гр} = (1,05  1,1)^.U_имп/n = (1,05  1,1)^.1600/4 = 420  440 кВ,

l₂^* = 55,0  60,0 см;

- Для промежутка l₃ минимальная длина составляет:

U_{расч.гр} = (1,05  1,1)^.U_имп/n = (1,05  1,1)^.1600/10 = 168  176 кВ,

l₃^* = 17,0  19,0 см;

- Для промежутка l₄ минимальная длина составляет:

U_{расч.гр} = (1,05  1,1)^.U_имп/n = (1,05  1,1)^.1600/8 = 210  220 кВ,

l₄^* = 21,0  22,0 см.

Для промежутков l₁ и l₅ значения U_{расч.гр} лежат далеко за пределами графической зависимости U_{расч.гр} = f(l) {5, стр.124, рис.3-15}, но судя по тенденции расчётов, значения l₁^* и l₅^* будут ниже соответствующих значений при проверке изоляционных промежутков l₁ и l₅ на воздействие разрядного напряжения промышленной частоты, а т.к. из расчётных значений l^* в конечном итоге выбирается наибольшее, то точную проверку l₁ и l₅ на грозовое воздействие можно не делать.

3.5. Расчёт промежутков внутренней изоляции

К промежуткам внутренней изоляции относятся l₆ и l₇. Проверка производится по формуле

l = U_р^._нп/(E_м.доп^.k_имп), где

U_р – расчётное значение разрядного напряжения (U_расч’, U_{расч.гр}’, U_{расч.ком}’);

_нп – коэффициент неоднородности поля, в данном случае _нп = 1,4;

E_м.доп -

IV. РАСЧЁТ ТОКОВЕДУЩЕЙ СИСТЕМЫ

В НОМИНАЛЬНОМ РЕЖИМЕ И ПРИ КЗ

4.1. Расчёт токовых характеристик ВК

4.1.1. Номинальный ток

Номинальный ток ВК – наибольший допустимый по условиям нагрева частей ВК ток нагрузки в продолжительном режиме, на который рассчитан ВК

I_ном = 2000 А.

4.1.2. Номинальный ток отключения

Номинальный ток отключения ВК – наибольший ток (действующее значение периодической составляющей) в момент размыкания контактов, на отключение которого рассчитан ВК при нормированных условиях его коммутационной способности

I_ном.о = 31,5 кА.

4.1.3. Апериодическая составляющая

Нормированное процентное содержание апериодической составляющей – наибольшее допустимое по коммутационной способности ВК отношение апериодической составляющей к амплитуде периодической составляющей номинального тока отключения ВК в момент размыкания контактов

_н = 47.

4.1.4. Сквозные токи КЗ

ВК во включенном положении должен выдерживать без повреждений, могущих препятствовать его исправной работе, электродинамическое и термическое воздействие сквозных и ударных токов КЗ

- Предельный сквозной ток КЗ

i _пс = 1,8^.2^.I _ном.о = 1,8^.2^.31,5 = 80,186 кА;

- Эффективное значение предельного сквозного тока КЗ

I _пс = i _пс/3 = 80,186/3 = 46,295 кА;

- Предельный ток термической стойкости

I _пс = I _ном.о = 31,5 кА;

- Время протекания предельного тока термической стойкости

T _пт = 2 c.

4.1.5. Ударные токи КЗ

- Ударный ток КЗ:

i _уд = i _пс = 80,186 кА;

- Эффективное значение ударного тока КЗ:

I _уд = i _уд/3 = 80,186/3 = 46,295 кА.

4.2. Расчёт кратковремённого нагрева токоведущих частей токами КЗ

Условие термической стойкости токоведущих частей: _к < _доп. Используя кривые адиабатического нагрева проводников  = f(A){6, стр.83}, можно найти температуру токоведущих частей в конце КЗ _к и сравнить её с предельно допустимой температурой нагрева _доп.

Значение коэффициента А при температуре _к определяется по формуле:

А_к = А_н + (I_т/F)^2.t_т, где

А_н – значение коэффициента А при температуре проводника перед началом КЗ _н, равной наибольшей допустимой температуре нагрева при длительной работе при номинальном токе;

А_к - значение коэффициента А при температуре проводника _н;

I_т - ток КЗ (термической стойкости), протекающий за время t_т = 2 сек.

Проверке подлежат

• Медный ламельный контакт ДУ

_н = 90С {ГОСТ 8024-84}, _доп = 300 С, А_н = 1,60^.10¹⁶ А^.сек/м² 

 А_к = 1,6^.10¹⁶ + (31500/0,00257)^2.2  1,65^.10¹⁶ А^.сек/м² 

_к = 120 С < _доп.

• Латунная токоведущая труба ДУ

_н = 60С {ГОСТ 8024-84}, _доп = 250 С, А_н = 0,40^.10¹⁶ А^.сек/м² 4

 А_к = 0,40^.10¹⁶ + (31500/0,003890)^2.2  0,50^.10¹⁶ А^.сек/м² 

_к = 145 С < _доп.

Рис 7. Тепловая модель ДУ ВВМ-500

4.3. Исходные данные для расчёта

нажатия в скользящем ламельном контакте

Исходные данные взяты из литературы {4}, {5}, {6}, таблицы 2.

- Номинальный ток выключателя I_ном = 2000 А;

- Максимальная температура контактов из меди и

медных сплавов _доп = 120 C;

- Превышение температуры контакта над температурой

удалённых точек  = 5 К;

- Количество ламелей m = 15;

- Количество точек касания для линейного контакта n = 2;

- Удельное сопротивление меди при 0 C ₀= 1,62^.10^-8 Ом^.м;

- Температурный коэффициент электрического

сопротивления меди при 0 C  = 0,00433 K^-1;

- Теплопроводность меди при 0 C ₀ = 388 Вт/(м^.К);

- Микротвёрдость меди при 0 C H = 730 МПа;

- Температура плавления меди ₀ = 1083 С;

- Температурный коэффициент электрического

сопротивления меди при 0 C  = 0,00433 K^-1;

- Коэффициент шероховатости поверхности _м = 1;

- Коэффициент неравномерности по точкам касания k_н = 1,1  1,3.

Предварительные расчёты:

 = ₀^.(1+_cu^._доп) = 1,62^.10^-8.(1 + 0,00433^.105) = 2,357^.10^-8 Ом^.м;

 = ₀^.(1 - _т^._доп) = 388^.(1 - 1,8^.10^-4.120) = 379,619 Вт/(м^.К);

_н = 273 + _доп = 273 + 120 = 393 К; _пл = 273 + _пл = 273 + 1083 = 1356 К;

H=H^.[1-(_н/_пл)^2/3]/[1-(273/_пл)^2/3]=730^.[1-(393/1356)^2/3]/[1-(273/1356)^2/3]; H = 622,5 МПа.

Расчёт контактного нажатия по сферической формуле:

F_к.сфр = [n^.(I_ном/(n^.m)^.k_н)^2.k_л^.^._м^.H_б]/[16^.^2.(аrccos(T_к/T_м))²];

F_к.сфр = [2^.(2000/(2^.15)^.1,2)^2.2,357  10^-8.3,14159^.3,7^.10⁸]/

/[16^.379,619^2.(аrccos(388/393))²];

F_к.сфр = 7,826 H.

Расчёт контактного нажатия по эллиптической формуле:

F_к.элп = [n^.(I_ном/(n^.m)^.k_н)^2.^.^._см]/[32^.^.(T_к - T_м)];

F_к.элп = [2^.(2000/(2^.15)^.1,2)^2.2,357^.10^-8.3,14159^.3,7^.10⁸]

/[32^.379,619^.(388 - 393)];

F_к.элп = 7,972 H.

4.4. Расчёт параметров скользящего

ламельного контакта ДУ программой {4}

- Исходные данные:

Исходные данные для расчёта взяты из {3}, {4}, {5}.

 Материал контактной пары латунь/медь;

 Номинальный ток 2000 А;

 Номинальный ток отключения 31500 А;

 Допустимая температура в номинальном режиме 120+273=393 К;

 Допустимая температура при КЗ 300+273=573 К;

 Температура плавления 1083+273=1356 К;

 Твердость по Бринелю при 0С 5^.10⁸ Н/м²;

 Теплопроводность 388 Вт/(м^.К);

 Длина ламели 0,051 м;

 Внутренний диаметр ламели 0,082 м;

 Внешний диаметр ламели 0,116 м;

 Сечение ламели 0,001785 м²;

 Число ламелей 15;

 Число точек касания 2.

- Результаты расчёта:

 В номинальном режиме сила контактной пружины 7,953 Н;

 В режиме короткого замыкания максимальная

температура точки касания 1247 К;

 Электродинамическая сила притяжения,

действующая на одну ламель 13,083 Н;

 Электродинамическая сила отталкивания,

действующая на одну ламель 6,830 Н;

 Фактическое нажатие 10,230 Н;

 Переходное сопротивление контакта 7,559^.10^-6 Ом;

 Тепловые потери в контакте 30,236 Вт.

4.5. Расчёт распределения температуры методом тепловых схем

Расчёт распределения температуры по длине стержневой системы, состоящей из нескольких участков (стержней), каждый из которых имеет постоянное сечение, основан на использовании метода тепловых схем. В практику тепловых расчётов вводится понятие «тепловой четырёхполюсник». Рассматривается стержневая система, состоящая из n участков. В этой системе выделяется j-й участок конечной длины, имеющий равномерно распределённый объёмный источник энергии и взаимодействующий с участками i (i = j - 1) и k (k = j + 1). Пусть в установившемся режиме теплообмена данный участок j воспринимает от участка i какое-то количество тепла (Q₁), передаёт участку k, количество тепла (Q₂), а с его боковой поверхности в окружающую среду уходит тепловой поток Q₂. Избыточные температуры на концах участка равны _ij _jk.

Рассмотренный случай взаимодействия j-го участка с соседними участками и с окружающей средой может быть представлен в виде симметричной Т-образной тепловой схемы – теплового четырёхполюсника, параметры которого (R_j’, R_j’’, _yj) таковы, что при заданных значениях _ij и _jk тепловые потоки Q₁, Q₂ и Q₃ сохраняют свои значения. Замена каждого участка стержневой системы подобной тепловой схемой и их соответствующее соединение даёт тепловую схему всей стержневой системы, при этом условия сопряжения на стыках соседних участков выполняются автоматически.

Полученную тепловую схему стержневой системы рассчитывают и находят избыточные температуры на концах каждого участка.

Далее устанавливается взаимосвязь между температурами на концах j-го участка (_ij и _jk) с распределением температуры по его длине, а также взаимосвязь между геометрическими и тепловыми параметрами j-го участка с элементами тепловой схемы. Для этого находится распределение температуры по длине j-го участка, причём известны и не зависят от температуры длина стержня L, избыточные температуры на его концах _ij и _jk, коэффициенты теплопроводности  и теплоотдачи k_экв, периметр S, сечение F и удельная мощность равномерно распределённого объёмного источника энергии W.

Этот случай описывается дифференциальным уравнением

d²/dx² – b^2. = - W/, b² = k_экв^.S/^.F,

решение его при граничных условиях _j(0) = _ij и _j(L) = _jk имеет вид:

_j(x) = (1/sh(b^.L))^.[(_ij - _yj)^.ch(L – x)^.b + (_jk - _yj)^.sh(b^.x)] + _yj

Из дифференциального уравнения находятся тепловые потоки Q₁ и Q₂

Q₁ = - ^.F^.(d/dx)_x=0 = (^.F^.b)/(sh(b^.L))^.[(_ij - _yj)^.ch(b^.L) - (_jk - _yj)];

Q₂ = - ^.F^.(d/dx)_x=L = (^.F^.b)/(sh(b^.L))^.[(_ij - _yj) - ch(b^.L)^.(_jk - _yj)].

Установившаяся температура, которую имел бы участок при отсутствии взаимодействия с другими участками

_yj = a²/b², а² = j^2./ + k_экв^.S^.₀/^.F;

_yj = (j^2.^.F + k_экв^.S^.₀)/(k_экв^.S).

Для тепловой схемы с использованием законов Кирхгофа

Q₁ – Q₂ – Q₃ = 0;

- _ij + Q₁^.R_j’ + Q₃^.R_j’’ + _yj = 0;

- _ij + Q₃^.R_j’’ + Q₂^.R_j’ + _ik = 0.

Решая систему уравнений относительно R_j’ и R_j’’, можно получить выражения для тепловых сопротивлений участков конечной длины

R_j’ = (ch(b^.L) – 1)/(^.F^.b^.sh(b^.L)); R_j’’ = 1/(^.F^.b^.sh(b^.L)).

Расчёт тепловых сопротивлений R_j’ и R_j’’, установившихся температур _yj участков системы сведём в таблицу 6.

Влияние контакта учитывается дополнительным подводом тепла

P_к = I_ном^2.R_к,

где R_к – переходное сопротивление контакта.

P_к = 2000^2.7,559^.10^-6 = 30,236 Вт;

Тепловая схема замещения токоведущей системы представлена в приложении. Для расчёта распределения температуры по длине токопровода методом тепловых схем используется программный пакет, разработанный на кафедре ТВН.

Таблица 6. Исходные данные для программного теплового расчёта

L - длина участка с однородной изоляцией;

S - периметр токоведущего стержня на участке однородности;

F - сечение токопровода на участке однородности;

 - коэффициент теплопроводности материала токопровода на участке;

j – плотность тока;

 - коэффициент теплопроводности материала токопровода на участке.

V. РАСЧЁТ ГАЗОДИНАМИЧЕСКИХ

ПРОЦЕССОВ В ДУ

ВВ представляет собой сложный пневматический аппарат автоматического действия, в котором все основные операции, связанные с его работой: гашение дуги, перемещение размыкающихся контактов и ряд других - осуществляются посредством сжатого воздуха. Из этого следует, что с тем или иным циклом работы такого выключателя связана совокупность газодинамических процессов, протекающих в отдельных элементах или одновременно, или в определённой последовательности.

Основными газодинамическими процессами в ВВ являются:

• Истечение сжатого воздуха из резервуаров, камер;

• Наполнение сжатым воздухом воздухопроводов, камер гашения дуги;

• Движение воздуха в трубах, отверстиях и насадках.

Ходом этих процессов непосредственно определяются наиболее важные эксплуатационные характеристики ВК (время отключения, время включения, дугогасящая способность, сброс давления в резервуаре и др.).

При рассмотрении газодинамических процессов в большом числе случаев задачу можно упростить, сделав следующие предположения:

• Истечение газа происходит адиабатически;

• Процесс истечения имеет установившийся характер;

• Потери на трение в большинстве случаев отсутствуют.

5.1. Расчёт динамики пневматического механизма ДУ ВВ

Во включенном состоянии ВВ, давление в колонке ДУ равно атмосферному, т.е. p₀ = p_а = 0,1 МПа. При подаче команды управления на отключение ВВ в течение менее 0,06 сек {3} контакты ДУ должны разойтись под воздействием давления сжатого воздуха, наполняющего в это время колонку камер ДУ. В момент, когда давление сжатого воздуха сравняется с давлением сопротивления со стороны поршневого механизма подвижного контакта ДУ, подвижный контакт придёт в движение.

Сила сопротивления сжатому воздуху Q_c

Q_c = Q_п + P_пч + Q_тр = 1765,197 + 112,776 + 50 = 1927,937 Н, где

Q_п - сила номинального контактного нажатия, Q_п = 180^.9,807 = 1765,197 Н;

P_пч - вес подвижных частей (буфера, поршневого кольца, пружины поршневого механизма и подвижного контакта), P_пч = 112,776 Н; {3}

Q_тр - сила трения в скользящем контакте, принимаем Q_тр = 50 Н.

Давление, при котором поршневое кольцо камеры ДУ начнёт перемещаться

p_тр = p₀ + Q_c/S = 0,1^.10⁶ + 1927,937/(5,027^.10^-3) = 0,483 МПа, где

S - активная площадь поршневого кольца камеры,

S = (/4)^.(d_н² – d_в²) = (3,142/4)^.(0,116² – 0,084²) = 5,027^.10^-3 м², где

d_н и d_в – соответственно, наружный и внутренний диаметры поршня {3}.

Давление сжатого воздуха в ДУ в первом приближении можно принять

p_t = p_тр + b^.t, где

b - постоянная нарастания давления наполнения ДУ, b = 600 сек^-1;

t – время протекания процесса.

Ход подвижных контактов

h(t)= S/(6^.10^-5.m_пч)^.b^.t³ = 5,027^.10^-3/(6^.10^-5.11,5)^.600^.t³ = 4,371^.10^3.t³, где

m_пч – масса подвижных частей (буфера, поршневого кольца, пружины поршневого механизма и подвижного контакта), m_пч  11,5 кг {3}.

Максимальное значение, на которое расходятся контакты ДУ при отключении ВВ h_макс = 0,040 м {3}. Время, за которое контакты разойдутся на эту величину можно определить из последней зависимости

t_дв = ³(6^.10^-5.11,5^.0,040)/(5,027^.10^-3.600) = 2,092^.10^-2 сек (20,920 мсек).

Скорость движения подвижного контакта описывается выражением

V(t)=S/(2^.10^-5.m_пч)^.b^.t²=5,027^.10^-3/(2^.10^-5.11,5)^.600^.t²,V(t)=1,311^.10^4.t², м/с

Графические зависимости V(t) и h(t) представлены на рис.8.

5.2. Выбор необходимого объёма резервуара

Расчёт ведётся по формуле:

V_мин = (0,57^.S^.с₀^.t)/ln(P_н/P_к)^1/k, где

S – площадь сечения выхлопных отверстий. На один полуполюс ВВ приходится четыре цилиндрических сопла диаметром d₁ = 0,055 м и двадцать конических отверстий диаметром d₂ = 0,015 м. Отсюда:

S = (/4)^.(₁^.4^.d₁² + ₂^.20^.d₂²), где

_1,2 - коэффициенты сужения струи отверстий: ₁ = 0,5, ₂ = 0,7;

S = (3,142/4)^.(0,5^.4^.0,055² + 0,7^.20^.0,015²) = 8,414^.10^-3 м²;

с₀ - скорость звука в воздухе при начальных условиях, с₀ = 356 м/сек;

t – время, в течение которого контакты разомкнуты и происходит свободное истечение воздуха из ДУ, t = t_бп = 0,3 сек; {3}

P_н – начальное давление в резервуаре P_н = 2,1 МПа; {3}

– давление в резервуаре после отключения, P_к = 1,9 МПа; {3}

k - показатель адиабаты, k = 1,4.

V_мин = (0,57^.8,414^.10^-3.356^.0,3)/ln(2,1/1,9)^1/1,4 = 2,651 м³.

По конструктивным соображениям объём резервуара полуполюса V = 3,6 м³.

5.3. Расчёт процесса наполнения камер ДУ сжатым воздухом

5.3.1. Исходные данные для расчёта

Исходные данные для расчёта взяты из {3} и непосредственно с конструкторских чертежей:

- Внутренний диаметр камеры ДУ d_кв = 0,208 м;

- Внутренний диаметр опорной колонки d_ив = 0,160 м;

- Высота колонки камер ДУ полуполюса h_к = 3,6 м;

- Высота опорной колонки h_и = 4,1 м;

- Диаметр отверстия главного дутьевого клапана d_дк = 0,170 м;

- Начальное давление воздуха в резервуаре p₀ = 2,0 МПа;

- Объём резервуара половины полюса 3,6 м³;

- Средний диаметр контактно-поршневого механизма d_м = 0,130 м.

Эффективное сечение отверстия главного дутьевого клапана

S₁ = (/4)^.^.d_дк ² = (3,142/4)^.0,45^.0,170² = 1,024^.10^-2 м², где

 - коэффициент сужения струи дутьевого клапана, принимаем  = 0,45.

Суммарное эффективное сечение отверстий контактных сопел

S₂ = 8,414^.10^-3 м², см. выше.

5.3.2. Расчёт наполнения ДУ при закрытых соплах в надкритическом режиме

Расчётная схема дана на рис.10. Объём, заполняемый сжатым воздухом

V₂ = (/4)^.(d_ив ^2.h_и + [d_кв² - d_м²]^.h_к),

V₂ = (/4)^.[0,160^2.4,1 + (0,208^.2 - 0,130²)^.3,6] = 0,157 м³.

Расчёт ведётся согласно уравнению {4, стр.288-289, ф.(10-7),(10-10)}

p_t = p_н^.(1 - ₁^.(₀/_н^k)^.t)^k, где

p_н = 0,1 МПа; T_н = 273 + 40 = 313 K; R = 293,7; c₀ = 355,6 м/сек.

_н = p_н/(R^.T_н) = 0,1^.10⁶/(293,7^.313) = 1,088 кг/м³;

₀ = p₀/(R^.T₀) = 2,1^.10⁶/(293,7^.313) = 22,844 кг/м³.

₁ = (0,57^.S₁^.c₀)/V₂ = (0,57^.1,024^.10^-2.355,6)/0,157 = 13,220 сек^-1.

При этом расчётная формула принимает вид

p_t = (10^-1)^.(1 + 268,363^.t)^1,4, МПа

По этой формуле рассчитана и построена начальная часть кривой рис.9. Надкритический режим заканчивается при p_t = 0,523^.p₀ = 1,098 МПа. Этому соответствует время t₁ = 16,907^.10^-3 сек.

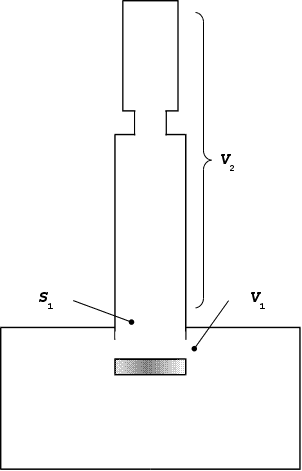
Рис.10. К расчёту первой стадии Рис.11. К расчёту второй стадии

наполнения камеры выключателя наполнения камеры выключателя

5.3.3. Расчёт наполнения при закрытых соплах в подкритическом режиме

Расчётная схема дана на рис.10. Давление рассчитывается по уравнению

 = _t



t_п = ₂^. (d_t/[_t^.(_t)], где (_t) = [2/(1 - k)^.(1 - ^{(k – 1)/k})],



 = 0,53

1/₂ = k^.S₁^.c₀/V₂ = 1,4^.1,024^.10^-2.355,6/0,157 = 32,470 сек^-1.

Расчёт ведётся графическим интегрированием {4, стр.290, рис.10-5}. Участок кривой также построен на рис.9. Длительность режима t₂ мала.

5.3.4. Расчёт второй стадии наполнения

По истечении времени t₂ происходит открытие контактных сопел ДУ и начинается вторая стадия наполнения. Расчётная схема дана на рис.11. В ходе этой стадии существенную роль играет имеющееся сужение воздушного тракта в месте перехода из дутьевой трубы в камеру. Учитывая это, следует считать за объём V₂ объём только внутренней полости камеры V₂’, за сечение S₁ – сечение входного отверстия из трубы в камеру S₁’.

В нашем случае

V₂’ = (/4)^.3,6^.(0,208² - 0,130²) = 0,075 м³;

S₁’ = ^.(/4)^.d_ив² = 0,45^.(3,142/4)^.0,16² = 9,048^.10^-3 м²;

S₂/S₁’ = 9,048^.10^-3/1,021^.10^-2 = 0,886  0,9.

Расчёт ведётся на основании уравнения {4, стр.292, ф.(10-23)}

 = _t



t_п = V₂’/(k^.S₁’^.c₀)^. (d_t/[_t^.() – 0,57^.(S₂/S₁’)^.^{(k – 1)/k}]



 = _н

Численное значение входящего множителя

V₂’/(k^.S₁’^.c₀) = 0,075/(1,4^.9,048^.10^-3.355,6) = 1,665^.10^-2 сек^-1.

Воспользовавшись графической зависимостью {4, стр.301, рис.10-12}

() = ^.() – 0,57^.(S₂/S₁’)^.^{(k – 1)/k},

по которой построена подынтегральная функция уравнения, представленного выше 1/() = f() {4, стр.301, рис.10-13}, при начальном значении _н = 1 - p_тр/p₀ = (2,1 - 0,483)/2,1 = 0,770 найдена зависимость _t = f₁(t)  p_t = _t^.p₀ = _t^.2,1^.10⁶ = f₂(t).

На рис.9 построен рассчитанный таким образом участок кривой, соответствующий второй стадии наполнения.

Этой стадии соответствует отрезок времени t₃. Процесс заканчивается в момент времени t₄ = t₁ + t₂ + t₃, когда происходит закрытие дутьевого клапана. В данном случае t₄ < 0,06 сек, что соответствует заявленному значению (см. таблицу 2) собственного времени отключения.

5.4. Расчёт истечения воздуха через сопло

при наличии в нём электрической дуги

При решении данной задачи принимаются следующие упрощения:

• Параметры неподвижного воздуха в камере не меняются;

• Тепловая энергия, выделяемая рассматриваемым участком ствола дуги, непрерывно поступает в газовый поток и равномерно распределяется по всему потоку;

• Рассматривается истечение газа без трения.

Для газового потока справедлив закон сохранения энергии, уравнение состояния, уравнение постоянства массового расхода. Из этих соотношений можно получить формулу для расчёта скорости газового потока

с₁ = 8600^.P₀^.S₂/N₀, {4, стр.155, ф.(5-80)}, где

P₀ – давление в камере к моменту зажигания дуги 1,6 МПа;

S₂ - суммарное эффективное сечение отверстий сопел S₂ = 8,414^.10^-3 м²;

N₀ – мощность дуги, равная количеству тепла, подводимого к единице массы газа в единицу времени

N₀ = u_д^.i_д, где

u_д – напряжение на рассматриваемой части ствола дуги, u_д  1000 В;

i_д – ток дуги, в качестве расчётного берётся амплитуда номинального тока отключения

i_д = 2^.I_ном.о = 2^.31,5 = 44,548 кА.

Скорость истечения на внешнем срезе сопла будет равна скорости звука c₀ = 20,1^.T₀ = 20,1^.(273 + 40) = 20,1^.313 = 355,6 м/сек {4, стр.288}.

с₁ = 8600^.1,6^.10^6.8,414^.10^-3/(1000^.44,548^.10³) = 25,989 м/сек.

При отсутствии дуги и расхождении контактов в сопле устанавливается критическая скорость истечения воздуха, равная 355,6 м/сек. При наличии дуги происходит быстрый нагрев воздуха в сопле и подъём давления. В результате скорость истечения воздуха падает; причём чем больше ток, тем сильнее торможение воздушного потока. При определённом значении тока происходит термодинамическая закупорка сопла, когда скорость воздуха падает до нуля. При закупорке сопла дуга не гаснет, т.к. отсутствует необходимый отвод теплоты от неё.

Экспериментально установлено, что для успешного гашения дуги необходимо, чтобы скорость воздуха не опускалась ниже 7-10 м/сек при амплитудном значении тока, что и имеет место в данном случае.

ЗАКЛЮЧЕНИЕ

Подводя итог своего курсового проекта, в ходе которого был произведён обзор ВВ, рассмотрены основные серии существующих в настоящий момент ВВ, описана конструкция и работа ВВМ-500, произведена проверка изоляции для этого ВК, выполнены токовые расчёты и описаны некоторые вопросы газодинамики ВВМ-500, хочу ещё раз выделить, на мой взгляд, основные причины отказов ВВ, которые и в настоящее время являются «проблемными»:

• Утечка сжатого воздуха через концевые и центральные дутьевые сопла ДУ из-за повреждений резиновых уплотнений;

• Самопроизвольное отключение полюсов ВК из-за дефектов клапанов отключения;

• Самопроизвольные включения;

• Разрушения пружин концевых сопел ДУ;

• Самопроизвольные понижения давления сжатого воздуха в системе с последующим самопроизвольным восстановлением.

Несмотря на значительный прогресс, достигнутый за последние годы в развитии элегазовых и совершенствовании маломасляных и вакуумных ВК, область применения ВВ пока ещё достаточно обширна. Следующие обстоятельства будут, по-видимому, способствовать даже расширению этой области в ближайшие годы:

• В ближайшие годы вряд ли можно ожидать, что токи отключения элегазовых и маломасляных ВК будут превышать 80-100 кА, особенно при напряжениях свыше 35 кВ, в то время как уже сейчас широко применяются генераторные ВВ с током отключения до 250 кА и требуются выключатели на напряжение свыше 750 кВ с током отключения до 100 кА;

• Из-за необходимости сжатия элегаза в процессе отключения и вследствие относительно низкой скорости истечения экономически нецелесообразно создавать эти ВК с временем отключения, меньшим, чем два периода, тогда как время отключения ВВ уже теперь технически доступными средствами может быть доведено до одного периода;

• Проблемы подогрева элегаза и поддержания высокой герметичности уплотнений при минусовых температурах определяют преимущества ВВ в районах с холодным климатом;

• Отключение токов КЗ вблизи мощных источников энергии с высоким содержанием апериодической составляющей также может быть пока осуществлено только ВВ.

Кроме того, даже без учёта этих обстоятельств при напряжениях свыше 420 кВ ВВ пока экономически более выгодны, чем ВК других типов.

ЛИТЕРАТУРА

1. Афанасьев В. В. Конструкции выключающих аппаратов. Л.: Энергия, Ленинградское отделение, 1969. – 640 с;

2. Афанасьев В. В., Вишневский Ю. И. Воздушные выключатели. Л.: Энергия, Ленинградское отделение, 1981. – 384 с;

3. Инструкция воздушных выключателей с воздухонаполненным отделителем серии ВВ-330, ВВ-500 и ВВМ-500 - Е.: Уралэлектротяжмаш, 1985;

4. Кукеков Г. А. Выключатели переменного тока высокого напряжения. Л.: Энергия, Ленинградское отделение, 1972. – 336 с;

5. Справочник по электрическим аппаратам высокого напряжения / Под редакцией В. В. Афанасьева. - Л.: Энергия, 1987. - 544 с;

6. Чунихин А. А., Жаворонков М. А. Аппараты высокого напряжения. М.: Энергоатомиздат, 1985. - 432 с;

7. Электрические аппараты высокого напряжения / Под редакцией Г. Н. Александрова. - Л.: Энергоатомиздат, 1989. - 344 с.

ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ

1. Математический пакет MathCAD 7.0. Copyright^ by MathSoft ^, 1997;

2. Операционная система DOS 7.0. Copyright^ by Microsoft ^, 1995;

3. Операционная система Windows’95. Copyright^ by Microsoft ^ 1995;

4. Программа расчёта контактных узлов CONT. Copyright^ by TVN, 1996;

5. Табличный процессор Excel 7.0. Copyright^ by Microsoft ^ 1997;

6. Текстовый редактор Word 7.0. Copyright^ by Microsoft ^ 1997.

ПРИЛОЖЕНИЕ

Sheet 1: Надкритический Режим