Федеральное агентство связи
ГОУ ВПО «Сибирский государственный университет
Телекоммуникаций и информатики»
Уральский технический институт связи и информатики (филиал)
Реферат на тему:
«Связь софистики и кибернетики»
Выполнила:
Студентка гр. ЭЕ-61
Скандаленко И.В.
Руководитель:
доцент кафедры ОГиСЭД, к.с.н.
Калугина Д.А.
Екатеринбург 2007
Содержание:
Введение 3
1. Софистика и софизмы 4
1.1 История софизма
1.2 Виды софизмов
1.3 Примеры софизмов
2. Булева алгебра 9
2.1 Джорж Буль
2.2 Булева алгебра
2.3 Некоторые свойства
2.4 Основные тождества
2.5 Примеры
2.6 Представления булевых алгебр
2.7 Аксиоматизация
3. Информатика и кибернетика 13
3.1 История кибернетики
3.2 Сфера кибернетики
Заключение 15
Источники 16
Введение
Мной взяты материалы сети Интернет.
Данная тема реферата выбрана не случайно, на мой взгляд, она позволит по-новому взглянуть на современную науку, связав её начала с более старшими научными и философскими течениями. Почему софистика и кибернетика, спросите Вы? Что ж отвечу, кибернетика представляется мне как перспективная молодая наука, с помощью которой можно будет ответить на многие вопросы человечества, и решить многие его проблемы, софистика же считается чуть ли не ложным философским течением, такой небольшой дурью древности, на мой взгляд, софистика - это философское течение, которое пыталось ответить на многие вопросы, используя при этом конечно нарушения законов логики, но, скорее всего всем известны какие-либо случаи из жизни, которые не поддаются логическому обоснованию. Также, на мой взгляд, существует некая связь между учениями древности и современными науками.
Объектом исследования является связь между кибернетикой и софистикой.
Предметом исследования является такое философское учение как софистика, высказывания - софизмы, философы – софисты.
Цель реферата : определение связей между современными научными течениями (кибернетика, информатика) с булевой алгеброй и затем с софистикой.
Главные задачи:
1. Изучить эти понятия.
2. Доказать, что софисты использовали в своих высказываниях логические связки.
3. Выявить, как Дж. Буль применял понятия логики в алгебре.
4. Определить связь между софистикой и булевой алгеброй.
5. Доказать связь булевой алгебры с современными научными течениями.
Кроме того, в реферате рассказывается о философах – софистах, даны наиболее интересные примеры софизмов, приводятся примеры булевой алгебры.
1 Софистика и софизмы
Понятие «Софистика» происходит от греч. «σοφιστική» — умение хитро вести прения. Философское течение в Древней Греции, созданное софистами.
Рассуждение, основанное на преднамеренном нарушении законов логики, на употреблении ложных доводов.
1. У чение представителей сложившейся в Афинах во второй половине 5 в. до н. э. школы софистов — философов-просветителей, тяготевших к релятивизму, первых профессиональных учителей по общему образованию.
Термин «софистика» происходит от греческого слова «софист» (sophistes — мудрец ), которым тогда называли платных учителей ораторского искусства.
Софи́сты (от др.-греч. σοφιστής - «умелец, изобретатель, мудрец, знаток»), термин, которым в древнегреческой литературе обозначали:
Умных, изобретательных, искусных, знающих людей, иногда людей специальной профессии;
В узком смысле — учителей мудрости и красноречия, философов 2-й половины V — 1-й половины IV вв. до н. э., которые впервые в Греции стали преподавать своё искусство за деньги.
Из сочинений софистов практически ничего не сохранилось. Изучение непрямых сведений усложняется тем, что софисты не стремились создать определенную цельную систему знаний. В своей дидактической деятельности они не придавали большого значения систематическому овладению учащимися знаниями. Их целью было научить учеников использовать приобретенные знания в дискуссиях и полемике. Поэтому значительный акцент производился на риторику.
В начале софисты учили правильным приемам доказательства и опровержения, открыли ряд правил логического мышления, но вскоре отошли от логических принципов его организации и все внимание сосредоточили на разработке логических уловок, основанных на внешнем сходстве явлений, на том, что событие извлекается из общей связи событий, на многозначности слов, на подмене понятий и т. д.
В античной софистике отсутствуют цельные течения. Учитывая историческую последовательность, можно говорить о «старших» и «младших» софистах. Старшие софисты (Протагор, Горгий, Гиппий, Продик, Антифонт) исследовали проблемы политики, этики, государства, права, языкознания. Все прежние принципы они подвергли сомнению, все истины объявили относительными. Релятивизм, перенесенный в теорию познания, привел софистов к отрицанию объективной истины.
В гносеологической концепции «старших» софистов абсолютизируются субъективный характер и относительность знания.
У «младших» софистов (Фразимах, Критий, Алкидам, Ликофрон, Нолемон, Гипподам) софистика вырождается в «жонглирование» словами, в фальшивые приемы «доказательства» истины и лжи одновременно.
2. Греч. soplnsma — измышление, хитрость — преднамеренное применение в споре и в доказательствах ложных аргументов, основанных на сознательном нарушении логических правил ; словесные ухищрения, вводящие в заблуждение.
Наиболее значительными софистами были Протагор, Горгий, Гиппий, Продик, Антифонт, Критий. Софисты не представляли собой единой группы ни по социально-политической ориентации (например, Протагор тяготел к рабовладельческой демократии, а Критий был врагом демократии), ни по отношению к предшествующей древнегреческой философии (Протагор опирался на идеи Гераклита, Горгий и Антифонт — на идеи элейской школы и т. п.), ни по их собственным философским идеям. Можно выделить некоторые общие черты философии софистов — перемещение философских интересов из сферы натурфилософии в область этики, политики, теории познания. Софисты призывали изучать самого человека и его субъективные особенности, часто доходя при этом до релятивизма и субъективизма. Идеи софистов вошли в древнегреческую философию как её необходимый составной элемент, их влияние заметно не только у Сократа, Платона и Аристотеля, у представителей мегарской школы и киников, но и во всей философии эллинизма, включая неоплатонизм.
Вырождение софистики началось уже в IV в. до н. э. (Евтидем и др.). Софисты постепенно превращались в фокусников, берущихся с помощью софизмов и др. способов (подробно описанных Аристотелем в «Софистических опровержениях») защищать или опровергать любые мнения.
Под именем «второй софистики» известно литературное течение II в. н. э., стремившееся реставрировать идеи и стиль греческой классики V—IV вв. до н. э. Оно отличалось учёностью, прекрасным знанием предшествующей греческой литературы; традиции Софистов в собственном смысле слова оно продолжило до некоторой степени только в лице Лукиана.
Таким образом, нас более интересуют старшие софисты, как философы связывающие философские понятия с теорий познания, использующие в философских понятиях логические связки, что мы рассмотрим в следующей графе.
1.1 История софизма
Софизм (от греч.σόφισμα, «мастерство, умение, хитрая выдумка, уловка») — ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм, в отличие от паралогизма, основан на преднамеренном, сознательном нарушении правил логики.
Аристотель называл софизмом «мнимые доказательства», в которых обоснованность заключения кажущаяся и обязана чисто субъективному впечатлению, вызванному недостаточностью логического или семантического анализа. Убедительность на первый взгляд многих софизмов, их «логичность» обычно связана с хорошо замаскированной ошибкой — семиотической: за счёт метафоричности речи, омонимии или полисемии слов, амфиболий и пр., нарушающих однозначность мысли и приводящих к смешению значений терминов, или же логической: подмена основной мысли (тезиса) доказательства, принятие ложных посылок за истинные, несоблюдение допустимых способов рассуждения (правил логического вывода), использование «неразрешённых» или даже «запрещённых» правил или действий, например деления на нуль в математических софизмах (Последнюю ошибку можно считать и семиотической, так как она связана с соглашением о «правильно построенных формулах».)
Вот один из древних софизмов («рогатый»), приписываемый Эвбулиду: «Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя рога» . Здесь маскируется двусмысленность большей посылки. Если она мыслится универсальной: «Всё, что ты не терял…», то вывод логически безупречен, но неинтересен, поскольку очевидно, что большая посылка ложна; если же она мыслится частной, то заключение не следует логически. Последнее, однако, стало известно лишь после того, как Аристотель создал логику.
А вот современный софизм, обосновывающий, что с возрастом «годы жизни» не только кажутся, но и на самом деле короче: «Каждый год вашей жизни — это её 1/n часть, где n — число прожитых вами лет. Но n + 1>n. Следовательно, 1/(n + 1)< 1/n».
Исторически с понятием «софизм» неизменно связывают идею о намеренной фальсификации, руководствуясь признанием Протагора, что задача софиста — представить наихудший аргумент как наилучший путём хитроумных уловок в речи, в рассуждении, заботясь не об истине, а об успехе в споре или о практической выгоде. (Известно, что сам Протагор оказался жертвой «софизма Эватла».) С этой же идеей обычно связывают и «критерий основания», сформулированный Протагором: мнение человека есть мера истины. Уже Платон заметил на то, что основание не должно заключаться в субъективной воле человека, иначе придётся признать законность противоречий (что, между прочим, и утверждали софисты), а поэтому любые суждения считать обоснованными. Эта мысль Платона была развита в аристотелевском «принципе непротиворечия» (см. Логический закон) и, уже в современной логике, — в истолкованиях и требовании доказательств «абсолютной» непротиворечивости. Перенесённая из области чистой логики в область «фактических истин», она породила особый «стиль мышления», игнорирующий диалектику «интервальных ситуаций», то есть таких ситуаций, в которых критерий Протагора, понятый, однако, более широко, как относительность истины к условиям и средствам её познания, оказывается весьма существенным. Именно поэтому многие рассуждения, приводящие к парадоксам и в остальном безупречные, квалифицируются как софизмы, хотя по существу они только демонстрируют интервальный характер связанных с ними гносеологических ситуаций. Так, софизм «куча» («Одно зерно — не куча. Если n зёрен не куча, то n + 1 зерно — тоже не куча. Следовательно, любое число зёрен — не куча») — это лишь один из «парадоксов транзитивности», возникающих в ситуации «неразличимости». Последняя служит типичным примером интервальной ситуации, в которой свойство транзитивности равенства при переходе от одного «интервала неразличимости» к другому, вообще говоря, не сохраняется, и поэтому принцип математической индукции в таких ситуациях неприменим. Стремление усматривать в этом свойственное опыту «нетерпимое противоречие», которое математическая мысль «преодолевает» в абстрактном понятии числового континуума (А. Пуанкаре), не обосновывается, однако, общим доказательством устранимости подобного рода ситуаций в сфере математического мышления и опыта. Достаточно сказать, что описание и практика применения столь важных в этой сфере «законов тождества» (равенства) так же, вообще говоря, как и в эмпирических науках, зависит от того, какой смысл вкладывают в выражение «один и тот же объект», какими средствами или критериями отождествления при этом пользуются. Другими словами, идёт ли речь о математических объектах или, к примеру, об объектах квантовой механики, ответы на вопрос о тождестве неустранимым образом связаны с интервальными ситуациями. При этом далеко не всегда тому или иному решению этого вопроса «внутри» интервала неразличимости можно противопоставить решение «над этим интервалом», то есть заменить абстракцию неразличимости абстракцией отождествления. А только в этом последнем случае и можно говорить о «преодолении» противоречия.
По-видимому, первыми, кто понял важность семиотического анализа софизмов, были сами софисты. Учение о речи, о правильном употреблении имён Продик считал важнейшим. Анализ и примеры софизмов часто встречаются в диалогах Платона. Аристотель написал специальную книгу «О софистических опровержениях», а математик Евклид — «Псевдарий» — своеобразный каталог софизмов в геометрических доказательствах.
Небольшое отступление: из данного текста видно, что софизмы являются определёнными логическими связками, а софисты используют в них не само понимание каких-либо предметов а логические понятия.
1.2 Виды софизмов:
а) софизм «учетверение термина» — силлогическое умозаключение, в котором нарушено правило простого категорического силлогизма: в каждом силлогизме должно быть только три термина. Умышленно ошибочное рассуждение строится с использованием нетождественных, но внешне сходных понятий: например, «Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего» ,
б) софизм недозволенного процесса — силлогистическое умозаключение, в котором нарушено правило простого категорического силлогизма: термин, не распределенный (не взятый во всем объеме) в одной из посылок, не может быть распределен (взят во всем объеме) в заключении: «все птицы имеют крылья — некоторые яйцекладущие имеют крылья» ;
в) софизм собирательного среднего термина — силлогистическое умозаключение, в котором нарушено правило простого категорического силлогизма: средний термин должен быть распределен (взят во всем объеме) по крайней мере в одной из посылок: «некоторые люди умеют играть на скрипке — все дипломаты-люди — все дипломаты умеют играть на скрипке» .
1.3 Примеры софизмов
1. Полупустое и полуполное:
Полупустое есть то же, что и полуполное. Если равны половины, значит равны и целые. Следовательно, пустое есть то же, что и полное.
2. Чётное и нечётное:
5 есть 2+3 («два и три»). Два — число чётное, три — нечётное, выходит, что пять — число и чётное и нечётное.
3. Не знаешь то, что знаешь:
«Знаешь ли ты, о чём я хочу тебя спросить?» — «Нет». — «Знаешь ли ты, что добродетель есть добро?» — «Знаю». — «Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь».
4. Лекарства:
«Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше».
5. Вор:
«Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего»
6. Отец — собака:
«Эта собака имеет детей, значит, она — отец. Но это твоя собака. Значит, она твой отец. Ты её бьёшь, значит, ты бьёшь своего отца и ты — брат щенят».
7. Рогатый:
«Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя рога».
2 Булева алгебра
2.1 Джордж Буль
Решающий вклад в алгебраизацию логики сделал английский ученный Джордж Буль (1815-1864). В 1847 году вышла его работа с характерным названием – “математический анализ логики, являющийся опытом исчисления дедуктивного рассуждения”. Применяя алгебру (в дальнейшем она стала называться булевой алгеброй), можно было закодировать высказывание, истинность и ложность которых требовалось доказать, а потом оперировать ими, как в математики оперируют с числами. Буль ввел три основные операции: И, ИЛИ, НЕ, хотя алгебра допускает и другие операции - логические действия . Эти действия бинарны по своей сути, т. е. они оперируют с двумя состояниями: ”истина” - “ложь”. Данное обстоятельство позволило в дальнейшем использовать булеву алгебру для описания переключательных схем.Необходимо отметить, что окончательное оформление и завершение булева алгебра получила в работах последователей Дж. Буля: У C. Джевонса и Дж. Венна (Англия), Э. Шредера (Германия), П. С. Порецкого (Россия).
Итак, булева алгебра использует логические связки, но и софистика также использует логические связки, их связь очевидна, попробуем определить связь булевой алгебры с современными науками.
2.2 Булева алгебра
Булевой алгеброй называется непустое множество A с двумя бинарными операциями
(аналог конъюнкции), 
(аналог дизъюнкции), унарной операцией
(аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:
 |
 |
ассоциативность |
 |
 |
коммутативность |
 |
 |
законы поглощения |
 |
 |
дистрибутивность |
 |
 |
дополнительность |
Первые три аксиомы означают, что (A, , ) является решёткой. Таким образом, булева алгебра может быть определена как дистрибутивная решётка, в которой выполнены две последние аксиомы. Структура, в которой выполняются все аксиомы, кроме предпоследней, называется псевдобулевой алгеброй.
Заметим, что булева алгебра использует бинарную систему как и информатика, что ж связь одного с другим очевидна, идем далее.
2.3 Некоторые свойства
Из аксиом видно, что наименьшим элементом является 0, наибольшим является 1, а дополнение ¬a любого элемента a однозначно определено. Для всех a и b из A верны также следующие равенства:
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
дополнение 0 есть 1 и наоборот |
 |
 |
законы де Моргана |
 |
инволютивность отрицания |
2.4 Основные тождества
В данном разделе повторяются свойства и аксиомы, описанные выше с добавлением еще нескольких.
Сводная таблица свойств и аксиом, описанных выше:
|
|
1 коммутативность |
|
|
2 ассоциативность |
| 3.1 конъюнкция относительно дизъюнкции |
3.2 дизъюнкция относительно конъюнкции |
3 дистрибутивность |
|
|
4 дополнительность (свойства отрицаний) |
|
|
5 законы де Моргана |
|
|
6 законы поглощения |
 |
 |
7 Блейка-Порецкого |
|
|
8 Идемпотентность |
|
9 инволютивность отрицания | |
|
|
10 свойства констант |
|
|
|
| дополнение 0 есть 1 |
дополнение 1 есть 0 |
|
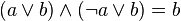 11-09-2015, 00:06 Разделы сайта |