Сложные и сложносокращенные силлогизмы
В процессе рассуждения простые силлогизмы выступают в логической связи друг с другом, образуя цепь силлогизмов, в которой заключение предшествующего силлогизма становится посылкой последующего. Предшествующий силлогизм называется просиллогизмом, последующий — эписиллогизмом
Соединение простых силлогизмов, в котором заключение предшествующего силлогизма (просиллогизма) становится посылкой последующего (эписиллогизма) называется сложным силлогизмом, или полисиллогизмом.
Различают прогрессивный и регрессивный полисиллогизмы. В прогрессивном полисиллогизме заключение просиллогизма становится большей посылкой эписиллогизма. Например:
В регрессивном полисиллогизме заключение просиллогизма становится меньшей посылкой эписиллогизма. Например:
Оба приведенных примера представляют собой соединение двух простых категорических силлогизмов, построенных по модусу ААА 1-й фигуры. Однако полисиллогизм может быть соединением большего числа простых силлогизмов, простроенных по разным модусам разных фигур. Цепь силлогизмов может включить в себя как прогрессивную, так и регрессивную связь.
Сложными могут быть чисто условные силлогизмы, которые имеют схему:
В символической записи:
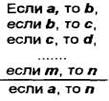
Из схемы видно, что, как и в простом чисто условном умозаключении, заключение представляет собой импликативную связь основания первой посылки со следствием последней.
В процессе рассуждения полисиллогизм принимает обычно сокращенную форму; некоторые из его посылок опускаются. Полисиллогизм, в котором пропущены некоторые посылки, называется соритом. Различают два вида соритов:
1. Прогрессивный полисиллогизм с пропущенными большими посылками эписиллогизмов. Например:
К сложносокращенным силлогизмам относится также эпихейрема. Эпихейремой называется сложносокращенный силлогизм, обе посылки которого являются энтимемами.
Например:
Развернем посылки эпихейремы в полные силлогизмы. Для этого восстановим в полный силлогизм сначала 1-ю энтимему:
Как видим, первую посылку эпихейремы составляют заключение и меньшая посылка силлогизма. Теперь восстановим 2-ю энтимему.
Вторую посылку эпихейремы также составляют заключение и меньшая посылка силлогизма.
Заключение эпихейремы получено из заключений 1-го и 2-го силлогизмов:
Развертывание эпихейремы в полисиллогизм позволяет проверить правильность рассуждения, избегать логических ошибок, которые могут остаться незамеченными в эпихейреме.
Понятие о логике высказываний
Современная символическая логика для анализа дедуктивных рассуждений строит особые логические системы; одна из них называется логикой высказываний или пропозициональной логикой, другая — логикой предикатов. Рассмотрим кратко принципы построения логики высказываний.
Логика высказываний — это логическая система, которая анализирует процессы рассуждения, основанные на характере связей между простыми суждениями, но без учета их внутренней структуры.
Язык логики высказываний включает: алфавит, определение правильно построенных выражений, интерпретацию.
Алфавит логики высказываний состоит из следующих символов.
Символы для высказываний: р, q, r,... (пропозициональные переменные).
Символы для логических связок:
(3) Технические знаки (,) — скобки.
Допустимые в логике высказываний выражения, называемые правильно построенными формулами или сокращенно ППФ, вводятся следующим определением:
1. Всякая пропозициональная переменная — р, q, r, ... является ППФ.
2. Если А и В — ППФ (А и В — символы метаязыка, выражающие любые формулы), то выражения — А
В, A
В, А→В, А
В, ˉ|А также являются ППФ.
Все другие выражения, помимо предусмотренных п. 1 и 2, не являются ППФ языка логики высказываний.
Логика высказываний может строиться табличным методом или как исчисление, т. е. как система, позволяющая получать из одних формул другие.
Табличное построение предполагает семантические определения пропозициональных связок в виде матриц, показывающих зависимость истинного значения сложных формул от значений их составляющих простых формул. Если А и В простые формулы, то истинное значение построенных с помощью логических связок сложных формул может быть представлено матричным способом — в виде таблицы.
Среди правильно построенных формул в зависимости от их истинностного значения различают тождественно истинные, тождественно ложные и выполнимые формулы.
Тождественно истинными называют формулы, принимающие значения истины при любых — истинных или ложных — значениях составляющих их пропозициональных переменных. Такие формулы представляют собой законы логики.
Тождественно ложными называют формулы, принимающие значение лжи при любых — истинных или ложных — значениях пропозициональных переменных.
Выполнимыми называют формулы, которые могут принимать значения истины или лжи в зависимости от наборов значений составляющих их пропозициональных переменных.
Табличное построение предполагает определение логических отношений между формулами. Существенное значение для анализа рассуждений имеет отношение логического следования (символ├), которое определяется следующим образом. Из Ai,..., An как посылок логически следует В как заключение, если при истинности каждого Ai, ..., Ап истинным является и В. В языке-объекте отношение следования адекватно выражается импликацией. Значит, если A1,..., Аn ,├ В, то формула, представляющая собой импликацию вида (A1 ^ А2 ^ ... ^ Аn) → В, должна быть тождественно истинной.
Табличное построение логики высказываний позволяет определять логические отношения между высказывания и проверять правильность умозаключений, используя приведенный выше критерий. В качестве примера предлагаем провести табличным способом проверку правильности рассуждения формы (p→q) ├ (ˉ|q→ˉ|p). Заменив знак логического следования между посылкой и заключением на импликацию и построив таблицу для полученной формулы, видим, что она является тождественно истинной. Значит, рассуждение является правильным.
Если в рассуждении содержится более трех переменных, то строить полную таблицу для проверки его правильности затруднительно и тогда используют сокращенный метод проверки, рассуждая от противного. Поскольку при правильном рассуждении формула вида (A1 ^ ... ^ Аn) → В должна быть тождественно истинной, посмотрим, не может ли она при каком-то наборе значений переменных оказаться ложной. Предположим, что может. Если из этого предположения получим какое-нибудь противоречие, то предположение неверно (и проверяемое рассуждение правильно), а если из этого предположения не получим противоречия, то увидим набор значений переменных, при котором формула ложна, т. е. тот набор, который опровергает проверяемое рассуждение.
Логика высказываний как исчисление — это прежде всего так называемая система натурального вывода (СНВ). Аппаратом в ней служат правила вывода, каждое из которых является какой-нибудь элементарной формой умозаключения. Переходя по этим правилам от посылок или некоторых допущений к новым формулам, постепенно доходят до заключения. Вывод из посылок осуществлен, если удалось элиминировать все сделанные допущения. Таким образом, под выводом формулы В (заключения) из формул A1 – An (посылок) имеется в виду последовательность формул, каждая из которых является либо посылкой, либо допущением, либо получается по правилам вывода из предыдущих и последняя формула этой последовательности есть формула В, а все допущения при этом элиминированы.
Правила СНВ позволяют оперировать со всеми связками, имеющимися в алфавите языка. Они делятся на правила введения (в) и правила исключения (и) связок.
Кроме этих прямых правил получения новых строк вывода, в СНВ приняты непрямые правила, определяющие стратегию построения вывода. Например, если нужно вывести из посылок формулу вида импликации (Х1→(X2 →... (Xn-1→Xn))), то после выписывания посылок выписываются в качестве допущений все антецеденты заключения, начиная с антецедента главного знака импликации, т. е. Х1,X2, X3...,Xn-1. Если при этом удастся вывести Xn, то по непрямому правилу
собираем последовательно формулы: (Xn-1→Xn)
(при этом исключается допущение Xn-1), (Xn-2→(Xn-1→Xn)(Xn-2 исключается из числа допущений) и т. д., пока ни получим требуемое заключение
X1→(Xn-2→…(Xn-1→Xn).
Это правило построения прямого вывода.
Приведем пример вывода с применением этого правила:
((рq)→r)├ (р→ (q├ r))
Другое непрямое правило используется для построения косвенного вывода, при котором допущением является отрицание В или отрицание последнего консеквента х„. Это правило имеет вид
и говорит о том, что если из каких-то формул (r) и допущения (А) получено противоречие (В ˉ|В), то из этих формул следует ˉ|А. Таким образом, если строится косвенный вывод формулы вида (X1→(X2→... (Xn-1→X n)...), то после посылок выписываются формулы:
Затем по правилам вывода получаем следствия из всех имеющихся посылок и допущений до тех пор, пока ни получим две противоречащие друг другу формулы (В и ˉ|В), что свидетельствует о несовместимости допущения косвенного доказательства с другими допущениями и посылками. Отсюда делается вывод о его ложности. Тогда в вывод вписывается строка ˉ|ˉ|Xnи тем самым допущение косвенного доказательства исключается. Например, осуществим косвенный вывод:
Косвенный вывод считается законченным, если в ходе вывода получена какая-то формула и ее отрицание, т. е. противоречие. Таким образом, если строится косвенный вывод формулы вида X1→(X2→...Xn), то построчно выписывают все антецеденты от X1 до Xn-1 в качестве допущений; в последней строчке выписывают отрицание последнего консеквента — ˉ|Xn как допущение косвенного вывода. По правилам вывода получаем различные следствия из всех имеющихся посылок и допущений. Получение двух противоречащих следствий говорит о ложности допущения косвенного вывода. На этом основании ДКД отрицается, т. е. получаем двойное отрицание. Снятие двойного отрицания дает формулу Xn.
Основными логическими свойствами системы натурального вывода являются ее непротиворечивость и полнота.
Непротиворечивость означает, что из истинных посылок могут получаться только истинные следствия и если формула выводима из пустого множества посылок, то она тождественно истинна. Это исключает возможность вывести из пустого множества посылок какую-либо формулу (А) и ее отрицание (ˉ|А). Полнота системы означает, что дедуктивных ее средств достаточно, чтобы вывести из пустого множества посылок любую тождественно истинную формулу.
Логика предикатов является более общей логической системой и включает логику высказываний как свою часть. Она располагает более эффективными логическими средствами для анализа рассуждений в естественном языке.
Задачі
1. Чи правильно визначені відношення між поняттями:
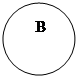А - фінансист;
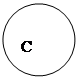В - державний службовець;
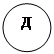С – спортсмен;
Д – студент?
Відповідь:
Поняття А, В, С і Д є порівнянні поняття, тому що спільне в них визначення особи, яка займається трудовою діяльністю, є родовою ознакою.
Із них сумісними поняттями є А і В (загальна видова ознака – наявність обов`язкової вищої освіти), С і Д (загальна видова ознака – надання права одночасно вчитись та професійно займатись спортом).
Поняття А і В несумісні з поняттям С, тому що для фінансиста заняття професійним спортом означає не заняття фінансами (прикладів суміщення в практиці не має), для державного службовця іншою професійною діяльністю (крім навчання і науково-педагогічної діяльності) заборонено законом.
Поняття А і В несумісні з поняттям Д, тому що поставлене питання розглядається в контексті однієї по кількості вищої освіти, тобто наявність вищої освіти виключає можливість навчання.
Таким чином, кола А і В не повинні пересікатись з колами С і Д.
Розглянемо сумісні поняття А і В.
В наведеному завдання між цими загальними поняттями існує відношення перехрещення, тому що їх видові ознаки не заперечують одна одну (наприклад, співробітник фінансового управління міністерства є одночасно і фінансистом, і державним службовцем).
Поняття А і В пересікаються правильно.
Розглянемо сумісні поняття С і Д.
Відношень тотожності тут не маємо, що очевидно, відношень підпорядкованості теж не маємо, тому що поняття студент розглядається по відношенню до понять А, В і С, а не окремого поняття С (наприклад, студент інституту фізичної культури).
Між цими загальними поняттями існує відношення перехрещення з тих же причин, що і між поняттями А і В.
Розглянемо несумісні поняття.
Між несумісними поняттями А і С, а також В і С існують відношення супідрядності, тому що вино входять, як було сказано вище, до одного роду – професія.
Між несумісними поняттями А і Д, а також В і Д існують відношення протилежності, тому що бути одночасно фінансистом (державним службовцем) з освітою і отримувати цю освіти неможливо.
Всі поняття (А,В,С,Д) є сумісними поняттями, враховуючи, що визначення цих понять показують відношення людини до трудової діяльності (родової ознаки).
По обсягу понять (розмір кіл Ейлера) визначено правильно.
Поняття „фінансист” більш об’ємне, ніж інші, існує в усіх галузях господарства.
Поняття „студент” повністю входить до обсягу поняття „державний службовець”, тому що по закону „Про державну службу” вища освіта обов’язкова.
2. Дайте реальне та номінальне визначення поняттям: Конституція, валюта, вулиця.
Відповідь:
Номінальні визначення понять.
Конституція – Основний закон держави.
Валюта – світові гроші.
Вулиця – місце прогулянок, або елемент плану забудівлі населеного пункту.
Реальні визначення понять.
Конституція – закон держави, який встановлює і регулює основні принципи життєдіяльності суспільства.
Валюта – грошова одиниця, що використовується як міжнародна розрахункова одиниця і є засобом обігу і платежу.
Вулиця – дорога, розташована між будівлями населеного пункту і призначена для проїзду транспорту і проходу пішоходів.
Валюта - світові гроші,
Обґрунтування: даному визначенні поняття „валюта” не розкривається його зміст, а з’ясовується ім’я цього поняття, тобто валюта – це гроші.
Вулиця – дорога
Реальні визначення понять
Конституція – нормативно-правовий документ, який встановлює і регулює державні правовідносини.
Валюта – засіб обігу і платежу в міжнародних і міждержавних розрахунках.
3. Визначте вид судження, терміни і їх розподіленість за допомогою “логічного квадрату”, утворіть інші судження, звернувши увагу на їх істинність:
Деякі приміщення потребують ремонту в цьому році.
Відповідь:
Логічний квадрат:
Усі приміщення потребують ремонту у цьому році |
А |
Е |
Жодне приміщення не потребує ремонту у цьому році |
| Деякі приміщення потребують ремонту у цьому році | І | О |
Деякі приміщення не потребують ремонту у цьому році |
Це істинне просте атрибутивне означене категоричне частково ствердне судження.
Істинне – тому що не має підстав вважати, що судження не відповідає тому, що є насправді.
Просте – тому що має один суб`єкт приміщення і один предикат потребують ремонту у цьому році.
Атрибутивне – тому що про предмет приміщення стверджується належність йому визначеної властивості потребують ремонту у цьому році.
Означене – тому що слово деякі має зміст тільки деякі, а не всі приміщення.
Категоричне – тому що форма ствердження в судження безумовна.
Частковоствердне– тому що за кількістю воно часткове деякі, а за якістю ствердне потребують.
Термін S (суб`єкт) приміщення нерозподілене, термін Р (предикат) потребують ремонту у цьому році розподілене, тому що обсяг предикату повністю включається в обсяг суб`єкту (приміщення бувають: які не потребують ремонту, які потребують ремонту і які відремонтовані).
Приймаємо судження І – істина, тоді по відношенню заперечення судження О – хиба. Якщо судження О – хиба, то по відношенню підпорядкування судження Е – хиба. Якщо судження Е – хиба, то по відношенню противності судження А може бути як істина, так і хиба. Але знаючи, що судження О – хиба, то по відношенню заперечення судження А – істина. Таким чином, А – істина, І – істина, Е – хиба, О – хиба.
По аналогії здійснюються міркування, якщо І – хиба.
Термін Р (предикат) „потребують ремонту у цьому році” – нерозподілене, тому що розподіленість предиката частковоствержувального судження встановити формально-логічними засобами неможливо і тому його вважають невизначеним і зараховують до нерозподілених ( М.Г. Тофтул. Логіка: пос.для студентів ВНЗ. – К.: ВЦ „Академія”, 2002. -368сю, стор.84).
Розглянемо ознаки істинності наведеного судження.
По умові задачі нам дано судження І. Яке воно істинне чи хибне?
Припустимо судження І – хиба → Е – істина → О – істина → А – хиба.
Але із хибності А неможливо зробити висновок про хибність І .
Отже, що І – хиба не доказано.
Припустимо судження І – істина → Е – хиба
Далі наступає невизначеність по всім напрямкам логічного квадрату і однозначного достовірного висновку про істинність або хибність даного судження неможливо.
4. Наведіть приклади судження, яке відповідає наведеній формулі. Складіть для нього таблицю істинності:
(В Ú С) → А
Відповідь:
Якщо заповнити з помилками реквізити адресата або несвоєчасно подати платіжне доручення в банк, то кошти банком не будуть перераховані адресату.
Заповнити з помилками реквізити адресата (В) – істина.
Несвоєчасно подати платіжне доручення в банк (С) – істина.
Отже, (В Ú С) – істина.
Кошти банком не будуть перераховані адресату (А) – істина.
Отже, (В Ú С) → А – істина.
| В | С | (В Ú С) | А | (В Ú С) → А |
| і | і | і | ||
| і | і | і |
5. Проаналізуйте з погляду дотримання формально-логічних законів наведені міркування:
Свідок А.: Фірма Н. не мала солідних ділових партнерів. Внаслідок цього вона не отримувала великих прибутків.
Свідок Б. Фірма С. має великий досвід роботи і солідний авторитет. Два роки тому вона підписала договір про співробітництво з фірмою Н., що принесло їм солідні прибутки.
Відповідь:
Міркування свідка А.
Закон тотожності виконується, тому що поняття солідний діловий партнер та отримання великих прибутків тотожні.
Закон суперечності не діє, тому що обидва судження не протилежні.
Закон виключеного третього
10-09-2015, 21:19