Понятие

- не богач». Уже из приведенных примеров ясно, чем различаются контрарность и контрадикторность. Еще отчетливее это раз­личие демонстрируется при помощи графических схем. Сумма объемов контрарных понятий (рис.4) не исчерпывает некоего универсального класса, поскольку имеется, по край­ней мере, одно состояние или свойство, занимающее сред­нюю позицию между ними (применительно к приведенным примерам: «не-молодость и не старость, а средний возраст», «не горячий, но и не холодный, а теплый или прохладный», и т. п.).

Рис.4.Контрарность понятий

Для контрадикторных понятий это среднее состояние или свойство исключено, сумма их объемов полностью ис­черпывает универсальный класс (рис.5). В самом деле, на­пример, понятие «не старость» относится ко всем периодам жизни, кроме старости (не только к молодости, но и к среднему возрасту). Поэтому оппозиция «старость - не старость» (в отличие от оппозиции «старость - молодость») исчерпывает все возрастные состояния. Любое из этих

состо­яний может быть отнесено к старости либо к не-старости.

Рис.5. Контрадикторность понятий

Q ( не-P )

Из сказанного ясно, что если дано какое-то понятие P , то образование контрадикторного по отношению к нему поня­тия осуществляется достаточно просто - посредством логи­ческого отрицания (не-P ). Образование же контрарного по­нятия затруднено некоей не всегда очевидной шкалой оце­нок, в соответствии с которой можно было бы выделить группы объектов, занимающих в данной предметной области полярные позиции. Во многих случаях построение такой шкалы без каких-либо добавочных условий невозможно. В этом можно убедиться, пытаясь образовать контрарную оп­позицию для таких, например, понятий, как торшер, книга, техническое редактирование и т. п.

В языке противоположным понятиям соответствуют ан­тонимы - слова с противоположными значениями. Явление антонимии исключительно многообразно, оно далеко не­однозначно отражает виды логической противоположности. Например, на первый взгляд кажется, что только контрадикторность (но ни в коем случае не контрарность) связана в языке с применением отрицательной частицы «не» (рис.5). Но логическое и грамматическое отрицание - не одно и то же. При ближайшем рассмотрении обнаруживают­ся пары контрадикторных понятий, словесная форма кото­рых не включает явного отрицания, скажем: «холостой - женатый». В то же время так называемое лексикализованное (слитое со словом) отрицание чаще всего выражает не контрадикторность, а контрарность, как это имеет место, например, в оппозиции «красивый - некрасивый».

Сложность логических и языковых механизмов, регули­рующих отношения антонимии, с одной стороны, затруд­няет контроль над смысловыми свойствами текста. С другой стороны, эта сложность - показатель богатства языка, ис­точник совершенствования речи в плане

выразительности. Из литературных (стилистических в широком смысле слова) приемов, использующих антонимию, назовем антитезу, ос­нованную на художественном «столкновении» противопо­ложных (чаще всего контрарных) понятий, Эффект анти­тезы хорошо иллюстрируется следующими стихами М. И. Цветаевой: «Не люби, богатый, - бедную,/Не люби, уче­ный, - глупую,/Не люби, румяный, - бледную, /Не люби, хоро­ший, - вредную!».

Подчинение (подчинённость).

Рис.6.Подчинение понятий

Если объем понятия Q целиком входит в объем понятия Р и составляет его часть, то Р называется понятием, подчи­няющим Q ,аQ - понятием, подчи­нённым Р (рис.6). Отношение подчинения (подчинённости) связывает такие, например, понятия: «редакти­рование» и «техническое редактирование», «издание» и «газета», «стихо­творение» и «стихотворение П. А. Вяземского "Ухаб"». Область пересе­чения таких понятий совпадает с объемом подчинённого понятия.

Если оба понятия общие, то подчиняющее называют ро­довым (или просто родом), а подчинённое -видовым (про­сто видом). Из приведённых в предыдущем абзаце примеров первые два иллюстрируют родовидовое отношение: техни­ческое редактирование - вид редактирования, газета - вид издания. В третьем примере подчиненное понятие - еди­ничное, поэтому родовидового отношения здесь нет.

Следует подчеркнуть, что логическая квалификация ка­кого-либо понятия как подчиняющего или подчинённого (для общих понятий - родового или видового) не является жесткой и теряет свое значение за пределами определенной пары множеств. Это, видно хотя бы из следующего отноше­ния: «издание» - «газета» - «спортивная газета». Понятие, занимающее в этой цепочке среднюю позицию, подчинено предыдущему (и является для него видовым), но подчиняет последующее (и значит, становится в данном звене родо­вым). Вообще, отношения подчинённости (подчинения) могут охватывать неопределённо большое число понятий, например: «Спаниель» - «охотничья собака» - «соба­ка» - «животное» и т. д.

Отношения между неопределенно большим количеством понятий.

Рис.7. Вариант отношения 4-х понятий

Если необходимо знать, какие отношения связывают не только два, но три, четыре, вообще, неопределенно большое число понятий, то по известному уже способу эта задача первоначально решается для каждой из имеющихся пар по­нятий, а затем полученные результаты сводятся в одну схему. Понятия Q , R , S (рис.7) связаны отношением внеположенности и в то же время подчинены Р. Такие понятия называ­ются соподчинёнными . Например, понятия «живопись», «графика», «ваяние» соподчинены понятию «вид изобрази­тельного искусства».

Нужно отметить, что с увеличением количества рассмат­риваемых понятий возрастают трудности в построении гра­фических схем, выражающих отношения между ними. Это и понятно: увеличивается число возможных областей пересечения классов, а значит, и тех «ячеек», которые должны на схеме соответствовать разным подмножествам.

Рис.8. Вариант отношения 4-х понятий

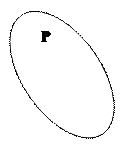
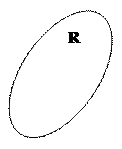Уже для четырех понятий, находящихся в отноше­нии перекрещивания, приходится прибегать к эллипсам, так как на круговых схемах некоторые из областей пересечения оказались бы утеряны. Например, отношение понятий «сту­дент», «спортсмен», «филателист», «москвич» изобразится схемой (рис.8). Можно насчитать 16 подмножеств, соот­ветствующих этому отношению: 1)студенты-спортсмены, за­нимающиеся филателией, и живущие в Москве; 2) студенты-спортсмены, занимающиеся филателией, но не живущие в Москве; 3) студенты-филателисты, живущие в Москве, но не занимающиеся спортом, …, 16) люди, не являющиеся ни студентами, ни спортсменами, ни филателистами, ни москви­чами.

Общая характеристика операций с понятиями.

Логические операции с понятиями - это такие действия, посредством которых из одного, двух или большего числа понятий образуется новое понятие. Иными словами, это действия, позволяющие определённым образом преобразо­вывать некоторые заданные множества.

Рис.10. Преобразование понятий

Рис.9. Преобразование понятий

Например, множе­ство студентов P и множество спортсменов Q могут быть мысленно преобразованы в класс, состоящий только из студентов, которые являются спортсменами. На рисунке 9 штриховкой показано множество, образованное посредст­вом данной операции. Эти же два множества можно под­вергнуть иной операции, получив класс спортсменов, ни один из которых не является студентом (рис. 10). Понятия, предшествующие операции, будем называть исходными, вновь полученное понятие назовем результатом соответст­вующей операции. В нашем примере исходными понятиями будут понятия «студент» и «спортсмен», результат же опе­рации в первом случае, вероятно, лучше всего выразить словосочетанием «студент - спортсмен», во втором - кон­струкцией «спортсмен, не являющийся студентом». Пораз­мыслив, можно прийти к выводу, что существуют и другие способы преобразования тех же исходных понятий, приво­дящие к различным результатам.

В различных эпизодах интеллектуально-речевой практи­ки (в различных текстах) встречаются понятия, словесная форма выражения которых позволяет рассматривать их как сложные, возникшие в результате преобразования других понятий. В таких случаях может возникнуть вопрос об исход­ных (иногда очевидных, иногда лишь предполагаемых) поня­тиях и характере произведенной с ними операции. Раскры­вая логические механизмы образования таких понятий, мы получаем возможность составить достаточно ясное представление об их содержании и объеме или, если необходимо, уточнить это представление. Рассмотренное выше понятие, выраженное словосочетанием «студент - спортсмен», недву­смысленно фиксирует область пересечения исходных клас­сов. Таковы же, например, понятия «солдат - герой России» или «журналист - международник». Первое выражает об­ласть пересечения класса солдат и множества героев России, второе - область пересечения понятий «журналист» и «спе­циалист по международным вопросам». Однако идеальная по ясности картина встречается далеко не всегда. Не столь просто охарактеризовать со стороны содержания и объема такие понятия, как, скажем, «научно-практическая конфе­ренция», «научно-техническая информация», «логико-психологический анализ», хотя они вроде бы построены по той же словообразовательной модели. Соединение некоторых исходных понятий в более сложную конструкцию не всегда осуществляется с должной степенью определённости, а иногда ведет к образованию достаточно серьёзных ошибок. Изучение логических операций с поня­тиями позволяет обнаружить внутренние, иногда скрытые механизмы подобных ошибок, способствует выработке дей­ственных навыков контроля над смысловыми свойствами текста. Объектами логических операций могут быть одно, два или неопределённо большое число понятий. Примерами ло­гических операций с одним понятием служат рассмотренные ранее операции обобщения и ограничения. Нужно отметить, однако, что есть ситуации, допускающие различные вариан­ты анализа. В понятии «симфония Д. Д. Шостаковича» оди­наково правомерно усматривать результат любой из следую­щих операций: 1) ограничение понятия «симфония», 2) ог­раничение понятия «музыкальное произведение Д. Д. Шос­таковича», 3) объединение указанных в пунктах 1 и 2 понятий способом, который позволяет зафиксировать в новом поня­тии область их пересечения.

Отрицание понятия.

Из операций с одним исходным понятием по степени значимости наибольшего внимания заслуживает операция, именуемая отрицанием . В результате отрицания произвольного понятия P образуется новое понятие не-P . Объем этого нового понятия включает в себя лишь те объек­ты х, о каждом из которых можно высказать истинное суж­дение х есть не-Р. Скажем, в результате отрицания понятия «журналист» получаем множество «не-журналистов», путем отрицания понятия «учебник» переходим к понятию «не-­учебник» и т. п. Чтобы отличить собственно логическое отрицание от не­которых грамматических форм, частица «не» отделяется от исходного понятия дефисом. Этим подчерки­вается, что в результате логического отрицания образуется понятие, связанное с исходным отношением контрадикторности, а не контрарности.

Рис.11. Отрицание понятия

н е-P

Смысл отрицания произвольного понятия Р хорошо передается графической схемой (рис.11), где прямоугольни­ком обозначен универсальный класс, а результат операции пока­зан штриховкой. Эта же схема де­лает наглядной закономерную за­висимость, выражаемую форму­лой не не-P =P . Формула показы­вает объемное равенство некото­рого понятия с результатом его двойного отрицания (так назы­ваемый закон двойного отрица­ния для классов). И действительно, исходному пункту;

поэтому двойное отрицание иног­да называется мнимым (дважды отрицая данное понятие, мы, по существу, его не отрицаем).

Сложение и умножение понятий.

Из операций с двумя исходными понятиями (или боль­шим их числом) следует выделить логическое сложение и логическое умножение. Результат сложения понятий Р и Q будем называть их логической суммой и обозначать P +Q , а результат умножения тех же понятий назовем их логическим произведением и обозначим Р•Q. Вобъём понятия Р+ Q входят те объекты, каждый из которых принадлежит хотя бы одному из исходных классов. Иными словами, х принадлежит классу Р+ Q , если истинно суждение х есть Р или Q (где союз «или» употребляется в неисключающем его значении). В объём понятия P •Q входят те объекты, каждый из которых принадлежит обоим исходным классам. Иначе говоря, х при­надлежит классу Р• Q если истинно суждение х есть P и Q , где союз «и» фиксирует одновременное вхождение х в дан­ные классы.

Различие между этими операциями иллюстрируют гра­фические схемы. На рисунках 12 - 15 показана логическая сумма, а на рисунках 16 - 19 - логическое произведение понятий Р и Q с учетом четырех известных нам видов отношений. Лишь для равнообъемных понятий итоги сложения и умножения со­впадают, в трех других случаях классы Р+ Q и Р• Q принци­пиально различны.

Это и понятно, поскольку операция сло­жения, в сущности, объединяет исходные множества, тогда как операция умножения образует класс, соответствующий области их пересечения. Уместно подчеркнуть, что результат умножения родового и видового понятий объёмно равен видовому, а результат сложения тех же понятий - родовому (см. рис.17 и 13). Если исходные понятия внеположенные, то их сложение образует класс, полностью включающий оба множества (см. рис.15); логическое произведение тех же понятий ведет к образованию нулевого класса (см. рис.19).

	Рис.17. Умножение подчинённых понятий
				Рис.16. Умножение равнообъёмных понятий

С теоретической точки зрения сопоставление классов P +Q и Р• Q представляет интерес для изучения двух суще­ственно разнящихся способов соединения некоторых произ­вольных множеств в новое (сложное) множество. Практи­ческий аспект проблемы имеет непосредственное отноше­ние к выбору союзов и других средств организации текста, при помощи которых несколько исходных смысловых еди­ниц объединяются друг с другом, образуя новое понятие. Пользуясь символическим языком, то есть, применяя ло­гические постоянные « + » и « • », мы легко улавливаем и точно фиксируем различие между сложением и умножением понятий. В естественном речевом общении (в нефор­мализованных текстах) объединение понятий не всегда дает достаточно ясную картину. Объясняется это следующими обстоятельствами. Во-первых, рассмотренные операции не исчерпывают всех возможных способов связи исходных по­нятий. Во-вторых, и это

главное, любые операции, включая сложение и умножение, могут выражаться различными средствами естественной речевой коммуникации. В логике договариваются читать выражение P + Q как Р или Q , а выражение Р• Q - как Р и Q , рассматривая союзы «или», «и» в качестве наиболее удачных словесных эквивалентов соответствующих операций. Однако в действительности не­редко используются и другие средства выражения этих опе­раций, в чем мы имели возможность убедиться на примере словосочетаний типа «студент-спортсмен», «журналист-международник» и т. п., где логическое умножение пред­ставлено дефисом. Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях созда­вать достаточно неопределенное представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил поль­зования городским транспортом: «Безбилетный проезд и бес­платный провоз багажа наказываются штрафом»? Предста­вим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них вой­дут пассажиры, не взявшие билета, в другое - не оплатив­шие провоз багажа. Если союз «и» рассматривать, как пока­затель логического умножения, то придется признать, что штраф должен быть наложен только на тех пассажиров, ко­торые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмот­ренной данным правилом, настолько ясен, что всякие раз­ночтения этой формулировки, вероятно, были бы признаны казуистикой, но все же использование союза «или» здесь следует признать предпочтительным. Аналогичный харак­тер носит следующая фраза: «Атеросклероз чаще всего по­ражает жителей больших городов и людей умственного труда». Исходные понятия «житель большого города» и «че­ловек умственного труда» находятся в отношении перекре­щивания. Вследствие недостаточной определенности их объединения в сложное понятие (оно выделено курсивом) воз­можны два варианта прочтения (истолкования, понимания) фразы: 1) атеросклероз чаще всего поражает жителей больших городов, занимающихся умственным трудом (логическое ум­ножение: см. рис.18); 2) атеросклероз чаще всего поражает вообще жителей больших городов или вообще людей умственного труда (ло­гическое сложение; см. рис.14). Поскольку второй вариант представляется более удач­ным для выражения данной мысли, и здесь также, вероятно, следовало бы отдать предпочтение союзу «или».

Умение находить правильные внешние формы для выра­жения логической суммы и логического произведения неко­торых исходных понятий определенным образом связано с продуктивностью смысловой и стилистической обработки текста. Обычно это умение проявляется в

виде автоматизи­рованных навыков, позволяющих найти и применить опти­мальную текстовую структуру в каждом конкретном случае. Но иногда интуиция нас подводит. Тогда полезно воспроиз­вести механизмы соответствующих операций (и даже прове­рить их графическими схемами). Об этом свидетельствует анализ некоторых типичных ошибок. Рассмотрим следую­щий фрагмент текста: «Милиционер, сержант милиции Б. оправился от ран и приступил к


10-09-2015, 22:29