Понятие

службе». Выделенная курси­вом часть фразы образована из двух исходных понятий, при­чем одно из них («сержант милиции »)является видовым по отношению ко второму («милиционер »). Напрашивается вывод о словесной избыточности выражения и целесообраз­ности его упрощения за счет одного из исходных понятий. Но, какой элемент конструкции может быть устранен без ущерба для информативности текста? Обратим внимание на тот факт, что Б. одновременно включается в класс сержантов милиции и в класс милиционеров. Таким образом, здесь перед нами, безусловно, логическое умножение. Но, как уста­новлено ранее, логическое произведение видового и родово­го понятий объемно равно видовому (см. рис.17). Следова­тельно, родовое понятие является избыточным и может быть устранено из текста, который должен выглядеть так: «Сер­жант милиции Б. оправился от ран и приступил к службе». И в самом деле, если Б. является сержантом милиции, то нет никакой нужды называть его еще и милиционером. Читате­лю предлагается подумать, почему иной вариант правки текста (устранение понятия «сержант милиции» при сохра­нении понятия «милиционер») связан с информационными потерями.

Неопределённые (размытые) понятия.

В интеллектуально-речевой практике функционирует множество понятий, обладающих достаточно ясным содер­жанием и резким объемом. Содержание понятия может счи­таться ясным, если известен входящий в него набор сущест­венных признаков. Объем понятия считается резким, если применительно к любому объекту однозначно решается во­прос, относится он к данному множеству или нет. Понятия с ясным содержанием и резким объемом принято называть определенными, а соответствующие множества - четкими или резкими. Но далеко не для каждого понятия его логичес­кие характеристики - содержание и объем - могут быть указаны с достаточной степенью точности. Понятия, не об­ладающие ясным содержанием и резким объемом, носят на­звание неопределенных или размытых (соответствующие множества часто именуются нерезкими или расплывчаты­ми). Различие между определенными и неопределенными понятиями легче всего показать путем соотнесения этих по­нятий с результатами их отрицания в пределах некоего уни­версального класса.

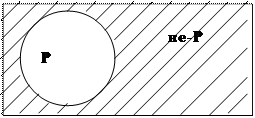
Рассмотрим с этой точки зрения понятие «гроссмейстер». На рисунке 20 универсальный класс представля­ет множество шахматистов и делится на два подмножества, соответствующих понятиям «гроссмейстер» (Р )и «не-гроссмейстер» (не-Р ). Второе из этих понятий образовано посред­ством отрицания первого. Подмножество гроссмейстеров характеризуется просто: в него входит тот и только тот, кто официально обладает этим шахматным званием.

	Рис.20. P и не- P -понятия с резким объёмом			Рис.21. Q и не- Q -понятия с нерезким объёмом

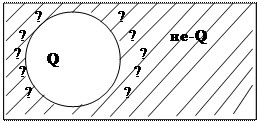
Столь же просто характеризуется подмножество не-гроссмейстеров: оно состоит из тех шахматистов, кому это звание не присвое­но. В универсальном классе эти два подмножества разделены резкой границей. Относительно любого шахматиста вопрос о том, является он гроссмейстером или нет, решается одно­значно и категорично. Понятие «гроссмейстер», безусловно, должно быть признано определенным. Теперь в том же универсальном классе (рис.21) таким же способом образуем контрадикторные понятия «хороший шахматист» (Q )и «тот, кто не является хорошим шахматис­том» (не-Q ).Казалось бы, рассматриваемая ситуация аналогична предыдущей, однако это не так. Вероятно, игра в силу гроссмейстера или мастера (быть может, кандидата в масте­ра, перворазрядника и т. д.) соответствует представлению о хорошем шахматисте, тогда как одно лишь знание правил шахматной игры - явно недостаточное условие для такой характеристики. Но ведь эти крайние точки, два полюса, между которыми имеется большой набор разнохарактерных оценок. Одни из оценок градуируют силу шахматистов в национальном или даже международном масштабе (шахмат­ные звания и разряды). Такие оценки официально закрепле­ны, и соответствующие им понятия имеют ясное содержание и резкий объем. Другие оценки не носят официального ха­рактера, однако, широко применяются в обиходе для харак­теристики любого шахматиста - от чемпиона мира до некое­го Ивана Ивановича, выходящего со своей доской на буль­вар, чтобы сразиться с соседом. Найти в этом наборе оценок резкую границу, отделяющую хороших

шахматистов от тех, кто не заслуживает такого названия, принципиально невоз­можно. Поэтому и объем рассматриваемого понятия недо­статочно резок. В универсальном классе образуется подмно­жество объектов, отнести которые к классам Q или не-Q в одинаковой степени затруднительно (на схеме это подмно­жество представлено зоной, отмеченной вопросительными знаками). «Хороший шахматист» типичный пример размы­того понятия.С размытыми понятиями мы встречаемся очень часто, и в этом нет ничего удивительного. Их существование обуслов­лено рядом постоянно действующих объективных и субъек­тивных обстоятельств. В распространённости размытых понятий можно убе­диться, попытавшись ответить на следующие вопросы. Если человек полнеет, то с какого именно момента он становится полным, с какого толстым и с какого тучным? Можно ли определить понятие «молодой специалист» точным указани­ем на стаж работы в данной области? Как отличить реку от ручья, руководствуясь обычным толкованием этих понятий, то есть исходя из того, что река — это «водный поток значи­тельных размеров», а ручей — «небольшой водный поток»? «Толстый», «тонкий», «молодой специалист», «опытный врач», и т.п. — все это недостаточно определенные понятия. Значительный слой размытых понятий связан с действу­ющими в определенной социальной среде системами цен­ностей и оценок (так называемые аксиологические понятия). Рассмотрим следующую ситуацию. Сообщение о том, что данный фильм цветной, содержит однозначную и объектив­ную информацию; сообщение, что тот же самый фильм пре­красен, не обладает аналогичной степенью определенности. Понятие «цветной фильм» имеет ясное содержание и резкий объем. Оценочное понятие «прекрасный фильм» не облада­ет ясным содержанием, оно является размытым и, в сущнос­ти, передает эмоциональное состояние того, кто считает фильм прекрасным.

ОГЛАВЛЕНИЕ.

ВВЕДЕНИЕ	2
СОДЕРЖАНИЕ ПОНЯТИЯ	3
Конкретные и абстрактные понятия	3
Относительные и абсолютные понятия	4
Положительные и отрицательные понятия	4
Собирательные и разделительные понятия	5
ОБЪЁМ ПОНЯТИЯ	6
Общие понятия	6
Единичные понятия	6
Пустые понятия	6
УНИВЕРСАЛЬНЫЙ КЛАСС	6
ОТНОШЕНИЕ МЕЖДУ ПОНЯТИЯМИ	7
Равнообъёмность понятий	7
Перекрещивание понятий	8
Внеположенность понятий	9
Подчинение понятий	11
ОТНОШЕНИЕ МЕЖДУ НЕОПРЕДЕЛЁННО БОЛЬШИМ КОЛИЧЕСТВОМ ПОНЯТИЙ	12
ОБЩАЯ ХАРАКТЕРИСТИКА ОПЕРАЦИЙ С ПОНЯТИЯМИ	12
Отрицание понятий	14
Сложение и умножение понятий	15
НЕОПРЕДЕЛЁННЫЕ ПОНЯТИЯ	18
ЛИТЕРАТУРА	22

ЛИТЕРАТУРА .

1. «ЛОГИКА И ТЕОРИЯ ОРГУМЕНТАЦИИ» В.Д.Евстратов, Г.К.Конык, издательство Казанского Государственного Технического Университета, 1999 г.

2. «ЛОГИКА» В.И.Курбатов, издательство «Феникс», 1996 г.

3. «ЛОГИКА» В.И.Свинцов, издательство «Скорина», 1998 г.

4. «ЛОГИКА: ЛОГИЧЕСКИЕ ОСНОВЫ ОБЩЕНИЯ» В.Ф.Берков, Я.С.Яскевич, В.И.Бартон и другие, издательство «Наука», 1994 г.

5. «ПРАКТИЧЕСКИЙ КУРС ЛОГИКИ ДЛЯ ГУМАНИТАРИЕВ» В.Н.Брюшинкин, издательство «Новая школа», 1996 г.

10-09-2015, 22:29