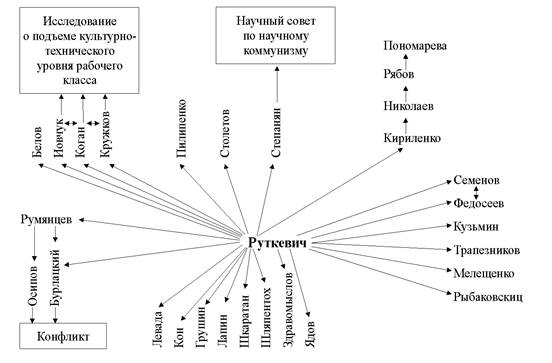
Рис. 5. Эгоцентрическая сеть члена-корреспондента РАН М.Н. Руткевича
В обобщенной сети можно выделить несколько "звезд". Это В.А. Ядов, Б.А. Грушин, Ю.А. Левада, Г.В. Осипов, М.Н. Руткевич. Опять же следует отметить, что речь идет не об их влиянии в профессиональном сообществе и, тем более, не о научных вкладах, а о репрезентации в биографических повествованиях, коллекция которых, разумеется, отражает коллективные представления части профессионального сообщества1. На основе обобщенной сети можно определить и контекст упоминания акторов, иными словами, можно подсчитать, что о ком говорят. В "положительные звезды" попадают В.А. Ядов, Б.А. Грушин, Ю.А. Левада. В "отрицательные" — М.Н. Руткевич, к Г.В. Осипову отношение менее однозначное. Можно детализировать задачу, показав, кто и в каком контексте говорит о "звездах", а также у кого какие "звезды". Контекст упоминаний о М.Н. Руткевиче получается достаточно отрицательным и связывается с так называемым погромом в Институте конкретных социальных исследований, который М.Н. Руткевич возглавил в начале 1970-х годов. Возможны и противоположные объяснения. Например, В.С. Семенов упоминает о М.Н. Руткевиче в положительном контексте. В.А. Ядова чаще всех упоминают В.В. Колбановский (10 раз), А.Г. Здравомыслов (6 раз), Б.А. Грушин (5 раз), Н.Ф. Наумова (5 раз), Г.В. Осипов (4 раза).
Таблица 1
Матрица смежных вершин (выделены сильные связи: 4)
| Колбановский | Ядов | Шубкин | Левада | Осипов | Кон | Заславская | Здравомыслов | Ольшанский | Карпинский | Грушин | Оников | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| Колбановский | 1 | | 10 | 3 | 7 | 17 | 3 | 2 | 4 | 1 | 1 | 5 | |
| Ядов | 2 | | 4 | 6 | 7 | 10 | 3 | 3 | 1 | 1 | 8 | ||
| Шубкин | 3 | 1 | | 1 | |||||||||
| Левада | 4 | | |||||||||||
| Осипов | 5 | 4 | 2 | 2 | | 1 | 1 | ||||||
| Кон | 6 | 2 | | ||||||||||
| Заславская | 7 | 1 | 7 | 1 | | ||||||||
| Здравомыслов | 8 | 6 | 1 | 3 | 1 | 2 | | ||||||
| Ольшанский | 9 | 1 | 1 | 1 | 1 | 6 | 2 | | |||||
| Карпинский | 10 | 3 | 1 | 3 | 8 | 2 | | 4 | |||||
| Грушин | 11 | 5 | 3 | 11 | 5 | | 2 | ||||||
| Оников | 12 | 2 | 2 | 2 | 6 | | |||||||
| Руткевич | 13 | 3 | 3 | 1 | 2 | 3 | 10 | ||||||
| Лапин | 14 | 3 | 8 | 11 | 2 | 1 | 1 | 1 | 5 | 1 | |||
| Рывкина | 15 | 2 | 5 | ||||||||||
| Коган | 16 | 1 | |||||||||||
| Наумова | 17 | 5 | 4 | 12 | 1 | 2 | |||||||
| Галкин | 18 | 1 | 2 | 1 | 4 | 3 | 2 | 3 | 2 | ||||
| Пилипенко | 19 | 1 | 3 | 3 | 6 | 3 | 2 | 2 | 1 | 3 | |||
| Фирсов | 20 | 3 | 1 | 2 | |||||||||
| Араб-Оглы | 21 | 1 | 2 | 1 | 4 | ||||||||
| Гордон | 22 | 1 | 1 | ||||||||||
| Давыдов | 23 | 1 | 1 | ||||||||||
| Бестужев | 24 | 1 | 4 | 1 | |||||||||
| Семенов | 25 | 3 | 3 | 2 | |||||||||
| ВСЕГО | 3 | 56 | 26 | 68 | 85 | 27 | 15 | 18 | 4 | 8 | 50 | 4 | |
Продолжение таблицы 1
| Руткевич | Лапин | Рывкина | Коган | Наумова | Галкин | Пилипенко | Фирсов | Араб-Оглы | Гордон | Давыдов | Бестужев-Лада | Семенов | ВСЕГО |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| 5 | 12 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 87 | ||
| 6 | 2 | 1 | 1 | 53 | |||||||||
| 1 | 3 | ||||||||||||
| 2 | 1 | 3 | |||||||||||
| 2 | 1 | 13 | |||||||||||
| 2 | |||||||||||||
| 4 | 6 | 19 | |||||||||||
| 2 | 1 | 16 | |||||||||||
| 1 | 13 | ||||||||||||
| 7 | 2 | 1 | 1 | 1 | 33 | ||||||||
| 8 | 2 | 6 | 1 | 1 | 44 | ||||||||
| 12 | |||||||||||||
| | 4 | 1 | 1 | 1 | 7 | 34 | |||||||
| 6 | | 3 | 1 | 1 | 44 | ||||||||
| 1 | | 8 | |||||||||||
| 7 | | 8 | |||||||||||
| 1 | 2 | | 1 | 29 | |||||||||
| 2 | 1 | | 1 | 22 | |||||||||
| 2 | 1 | 1 | 1 | 2 | | 1 | 1 | 1 | 34 | ||||
| | 6 | ||||||||||||
| | 4 | 1 | 13 | ||||||||||
| 5 | | 7 | |||||||||||
| 2 | | 5 | |||||||||||
| 1 | 1 | | 8 | ||||||||||
| 6 | | 14 | |||||||||||
| 68 | 28 | 10 | 6 | 8 | 6 | 2 | 9 | 7 | 5 | 3 | 14 | 530 |
Таблица 2
Матрица смежных вершин (выделены взаимные связи)
| Колбановский | Ядов | Шубкин | Левада | Осипов | Кон | Заславская | Здравомыслов | Ольшанский | Карпинский | Грушин | Оников | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| Колбановский | 1 | | 10 | 3 | 7 | 17 | 3 | 2 | 4 | 1 | 1 | 5 | |
| Ядов | 2 | | 4 | 6 | 7 | 10 | 3 | 3 | 1 | 1 | 8 | ||
| Шубкин | 3 | 1 | | 1 | |||||||||
| Левада | 4 | | |||||||||||
| Осипов | 5 | 4 | 2 | 2 | | 1 | 1 | ||||||
| Кон | 6 | 2 | | ||||||||||
| Заславская | 7 | 1 | 7 | 1 | | ||||||||
| Здравомыслов | 8 | 6 | 1 | 3 | 1 | 2 | | ||||||
| Ольшанский | 9 | 1 | 1 | 1 | 1 | 6 | 2 | | |||||
| Карпинский | 10 | 3 | 1 | 3 | 8 | 2 | | 4 | |||||
| Грушин | 11 | 5 | 3 | 11 | 5 | | 2 | ||||||
| Оников | 12 | 2 | 2 | 2 | 6 | | |||||||
| Руткевич | 13 | 3 | 3 | 1 | 2 | 3 | 10 | ||||||
| Лапин | 14 | 3 | 8 | 11 | 2 | 1 | 1 | 1 | 5 | 1 | |||
| Рывкина | 15 | 2 | 5 | ||||||||||
| Коган | 16 | 1 | |||||||||||
| Наумова | 17 | 5 | 4 | 12 | 1 | 2 | |||||||
| Галкин | 18 | 1 | 2 | 1 | 4 | 3 | 2 | 3 | 2 | ||||
| Пилипенко | 19 | 1 | 3 | 3 | 6 | 3 | 2 | 2 | 1 | 3 | |||
| Фирсов | 20 | 3 | 1 | 2 | |||||||||
| Араб-Оглы | 21 | 1 | 2 | 1 | 4 | ||||||||
| Гордон | 22 | 1 | 1 | ||||||||||
| Давыдов | 23 | 1 | 1 | ||||||||||
| Бестужев | 24 | 1 | 4 | 1 | |||||||||
| Семенов | 25 | 3 | 3 | 2 | |||||||||
| ВСЕГО | 3 | 56 | 26 | 68 | 85 | 27 | 15 | 18 | 4 | 8 | 50 | 4 | |
Продолжение таблицы 2
| Руткевич | Лапин | Рывкина | Коган | Наумова | Галкин | Пилипенко | Фирсов | Араб-Оглы | Гордон | Давыдов | Бестужев-Лада | Семенов | ВСЕГО |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| 5 | 12 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 87 | ||
| 6 | 2 | 1 | 1 | 53 | |||||||||
| 1 | 3 | ||||||||||||
| 2 | 1 | 3 | |||||||||||
| 2 | 1 | 13 | |||||||||||
| 2 | |||||||||||||
| 4 | 6 | 19 | |||||||||||
| 2 | 1 | 16 | |||||||||||
| 1 | 13 | ||||||||||||
| 7 | 2 | 1 | 1 | 1 | 33 | ||||||||
| 8 | 2 | 6 | 1 | 1 | 44 | ||||||||
| 12 | |||||||||||||
| | 4 | 1 | 1 | 1 | 7 | 34 | |||||||
| 6 | | 3 | 1 | 1 | 44 | ||||||||
| 1 | | 8 | |||||||||||
| 7 | | 8 | |||||||||||
| 1 | 2 | | 1 | 29 | |||||||||
| 2 | 1 | | 1 | 22 | |||||||||
| 2 | 1 | 1 | 1 | 2 | | 1 | 1 | 1 | 34 | ||||
| | 6 | ||||||||||||
| | 4 | 1 | 13 | ||||||||||
| 5 | | 7 | |||||||||||
| 2 | | 5 | |||||||||||
| 1 | 1 | | 8 | ||||||||||
| 6 | | 14 | |||||||||||
| 68 | 28 | 10 | 6 | 8 | 6 | 2 | 9 | 7 | 5 | 3 | 14 | 530 |
Рис. 6. Схема сильных связей в научном сообществе: максимальное остовное дерево, 23 вершины, 39 связей
В этой же матрице можно решить другую задачу: выделить не самые сильные, а взаимные упоминания (табл. 2). Сеть взаимодействий в этом случае значительно меняется. Во-первых, ее структура принимает двухполюсный вид. Сопоставив веса с контекстами, можно видеть некий аналог черно-белого изображения: "положительный" полюс представлен В.А. Ядовым, "отрицательный" — М.Н. Руткевичем. Такая сеть может показаться более информативной. Другие фигуры распознаются на черно-белом фоне не столь отчетливо. Так, несмотря на то, что Ю.А. Леваду упоминали многие информанты, он упомянул лишь немногих из них, поэтому его "звездность" отображается в сети взаимных упоминаний слабее, чем в сети сильных упоминаний. Г.В. Осипов, В.С. Семенов, Н.Ф. Пилипенко занимают промежуточное место между двумя полюсами. Сеть, построенная по принципу выделения взаимных связей (рис. 7), дает больше возможностей для применения числовых методов анализа. В частности, в данном случае можно не учитывать направление связей (сеть "взаимная") и перемещаться по сети в любом направлении. В ней нет тупиковых "висячих" вершин, в которые можно попасть при прохождении графа. Тем самым становится реализуемой задача применения таких свойств сети, как центральность и эквивалентность позиций акторов. Структурные индикаторы центральности и эквивалентности разработаны для неориентированных графов, и, применяя их, можно отказаться от весовых коэффициентов. Наличие/отсутствие связи кодируется соответственно как 1 или 0.
Центральность — местоположение актора относительно других акторов. Имеются многообразные определения центральности [9]. В одном случае центральной считается вершина, связанная с наибольшим количеством других акторов (степень центральности). В другом случае под центральной имеется в виду вершина, которая находится наиболее близко ко всем остальным вершинам (плотность центральности). В третьем случае, чем большее количество потоков перемещаемых ресурсов контролирует вершина, тем более центральной она является (посредничество центральности). Решаемая нами задача основана на третьем определении центральности.
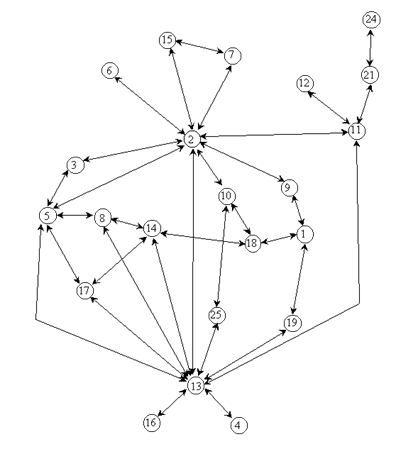
Рис. 7. Схема взаимных связей в научном сообществе (22 вершины, 35 связей)
Мы можем рассчитать центральность актора по формуле Шимбелла-Питтса. Здесь центральность рассматривается как посредничество:
CB (ni)= 
, i j,k (1)
— ненормированный показатель центральности актора ni, где:
gjk – общее число кратчайших путей между вершинами nj и nk ;
gjk(ni) – число кратчайших путей между вершинами nj и nk, которые проходят через вершину ni;
i отлично от j и k.
Идеология процедуры состоит в следующем: в связном графе из любой вершины можно попасть в любую другую вершину одним или несколькими путями. Если путей несколько, то путь, который включает наименьшее количество ребер, называют кратчайшим.
Кратчайших путей тоже может быть несколько. Так, от Осипова к Лапину (имена являются обозначениями вершин) мы можем пройти следующими кратчайшими маршрутами: Осипов — Ядов — Лапин; Осипов — Здравомыслов — Лапин; Осипов — Наумова — Лапин; Осипов — Руткевич — Лапин.
Тогда одно слагаемое в формуле (1) для Ядова будет равно 1/4, так как им "контролируется" одна четвертая всех кратчайших маршрутов.
Рассчитаем центральность для Ядова и сравним с центральностью Грушина:
CB (n2)=103 — ненормированная центральность Ядова.
CB (n11)=56 — ненормированная центральность Грушина.
Мы видим, что центральность Ядова в два раза выше, чем центральность Грушина, хотя, казалось бы, и Ядов, и Грушин полностью "контролируют" кратчайшие пути трех вершин, Ядов — пути Кона, Рывкиной и Заславской, а Грушин — пути Оникова, Араб-Оглы и Бестужева-Лады. Что такое "полностью контролируют кратчайшие пути"? Это значит, что все связи (допустим, Кона) со всеми остальными вершинами графа будут проходить только через Ядова, поэтому соответствующее слагаемое в формуле (1) будет равно 1/1.
Чтобы сравнивать центральности разных акторов более корректно, оценку следует стандартизовать. Так, максимальное количество связей между всеми вершинами графа равно 
. Соответственно, нормированная центральность будет рассчитываться по формуле:
C’B (ni) = 
(2)
В нашем случае g=22 и нормировка равна 210. Значения нормированного показателя C’B (ni) лежат в пределах от 0 до 1. Чем больше C’B (ni), тем более центральной является эта позиция.
Рассчитаем нормированные показатели центральности для Ядова и Грушина:
C’B (n2)=103,5833/210=0,4933 — нормированная центральность Ядова;
C’B (n11)=56/210=0,2666 – нормированная центральность Грушина.
Эквивалентность показывает, насколько похожи акторы по своим сетевым свойствам (их местоположению в сети, связям с другими акторами, сетевым ролям). Эквивалентность — это сетевое сходство двух акторов. Эквивалентность рассчитывается по формуле эвклидова расстояния. Пусть xik — количество связей между i-м и k-м акторами. Мы определяем дистанцию структурной эквивалентности для акторов i и j как эвклидово расстояние связей между этими акторами. Для акторов i и j это расстояние между i-й и j-й строкой и i-м и j-м столбцом социоматрицы.
Каждый актор описывается двумя компонентами социоматрицы — уникальными строкой и столбцом. Актор i описывается i-й строкой и i-м столбцом. Актор j описывается j-й строкой и j-м столбцом. Таким образом, эвклидово расстояние между акторами i и j — это кумулятивная разница (непохожесть) между каждой парой ячеек в строках i и j и каждой парой ячеек в столбцах i и j:
dij=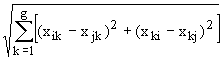 
, для i k, j k (3)
Если акторы i и j структурно эквивалентны, тогда их соответствующие строки и столбцы в социоматрице будут идентичны, и эвклидово расстояние будет равно нулю. Чем они меньше схожи структурно, тем больше будет эвклидово расстояние. Вообще, для любого графа эвклидово расстояние изменяется в пределах 0 dij<
, где g — размер матрицы (количество вершин в графе). В нашем графе взаимно ориентированных связей верхняя граница эквивалентности будет равна 6,32 (
=
=6,3245).
Тем не менее, сеть взаимных выборов желательно рассматривать совместно с сетью самых сильных связей.
Расширение общей сети акторов
Мы можем достроить сеть самых сильных связей, включив в нее акторов, которые не принимали участия в опросе, не были проинтервьюированы, но которых достаточно часто упоминали "актуальные" акторы-информанты.
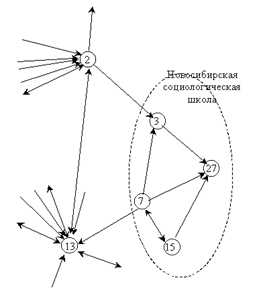
Рис. 8. Пример дополнения сети новыми вершинами
Логичным представляется взять за основу сеть самых сильных связей, потому что при отсутствии взаимности мы можем добавить самые сильные связи, направленные на других акторов. Все новые акторы будут находиться в плоскости акторов, и на них также будут направлены связи от артефактов. Процедурная последовательность такова: мы достраиваем социоматрицу, добавляя в нее новые столбцы — для тех акторов, которых называют чаще всего.
Таблица 3
Матрица смежных вершин: акторы "второго порядка"
| Амбарцумов | Аганбегян | Андреева | Бурлацкий | Замошкин | Зворыкин | Зиновьев | Ильенков | Иовчук | Капелюш | Карякин | Квасов | ||
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | ||
| Колбановский | 1 | 1 | 2 | 4 | 1 | 2 | 4 | 3 | 1 | ||||
| Ядов | 2 | 3 | 4 | 1 | |||||||||
| Шубкин | 3 | 4 | 1 | ||||||||||
| Левада | 4 | 1 | |||||||||||
| Осипов | 5 | 1 | 2 | 1 | 3 | ||||||||
| Кон | 6 | 1 | |||||||||||
| Заславская | 7 | 13 | 3 | ||||||||||
| Здравомыслов | 8 | 2 | 1 | ||||||||||
| Ольшанский | 9 | 1 | 2 | ||||||||||
| Карпинский | 10 | 1 | 8 | 1 | 2 | 2 | |||||||
| Грушин | 11 | 1 | 1 | 1 | 6 | 1 | 3 | 1 | 1 | ||||
| Оников | 12 | 1 | |||||||||||
| Руткевич | 13 | 6 | 3 | ||||||||||
| Лапин | 14 | 2 | 1 | 1 | |||||||||
| Рывкина | 15 | 3 | |||||||||||
| Коган | 16 | 1 | 34 | ||||||||||
| Наумова | 17 | 1 | 1 | 2 | 1 | 2 | |||||||
| Галкин | 18 | 8 | 2 | ||||||||||
| Пилипенко | 19 | 2 | 1 | 2 | 2 | 1 | |||||||
| Фирсов | 20 | ||||||||||||
| Араб-Оглы | 21 | 1 | 1 | 2 | 1 | ||||||||
| Гордон | 22 | ||||||||||||
| Давыдов | 23 | 2 | 14 | 2 | 2 | ||||||||
| Бестужев-Лада | 24 | 2 | 1 | 1 | |||||||||
| Семенов | 25 | 1 | 2 | 4 | |||||||||
| ВСЕГО | 6 | 21 | 10 | 43 | 10 | 7 | 13 | 20 | 47 | 5 | 5 | 17 | |
Продолжение таблицы 3
| Келле | Константинов | Мамардашвили | Нейгольдберг | Пруденский | Румянцев | Смирнов | Трапезников | Федосеев | Файнбург | Францев | Фролов | Харчев | Шляпентох | Щедровицкий |
| 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 |
| 1 | 2 | 8 | 4 | 1 | 9 | 1 | ||||||||
| 2 | 4 | 1 | 1 | |||||||||||
| 11 | 1 | 6 | ||||||||||||
| 2 | 3 | 1 | 1 | 2 | 4 | |||||||||
| 2 | 11 | 12 | 2 | 5 | ||||||||||
| 1 | 1 | 1 | 3 | |||||||||||
| 1 | 1 | 1 | 1 | |||||||||||
| 1 | 1 | |||||||||||||
| 26 | 3 | 1 | ||||||||||||
| 3 | 1 | 4 | 4 | 11 | 2 | 1 | 5 | 2 | 3 | |||||
| 1 | 3 | |||||||||||||
| 1 | 1 | 18 | 2 | |||||||||||
| 2 | 2 | 7 | 2 | 4 | 3 | 2 | 1 | |||||||
| 4 | 1 | |||||||||||||
| 4 | 1 | 7 | ||||||||||||
| 4 | 4 | |||||||||||||
| 1 | 23 | 9 | ||||||||||||
| 2 | 1 | 2 | 1 | |||||||||||
| 1 | 4 | 2 | 8 | 3 | 1 | 1 | ||||||||
| 1 | 1 | |||||||||||||
| 2 | 3 | |||||||||||||
| 1 | 10 | 1 | 1 | 1 | ||||||||||
| 1 | 1 | 1 | 7 | 8 | 1 | |||||||||
| 8 | 12 | 14 | 5 | 20 | 123 | 8 | 12 | 55 | 12 | 18 | 7 | 8 | 18 | 9 |
Так, Румянцева упомянули в сумме 123 раза, Федосеева – 55 раз, Иовчука — 47 раз, Бурлацкого — 43 раза. Частота упоминания остальных акторов — около 20 раз. В табл. 3 новые акторы перечислены в алфавитном порядке. Например, Аганбегяна (номер вершины 27) упоминали 4 человека: Шубкин — 4 раза; Осипов — 1 раз, Заславская — 13 раз; Рывкина — 3 раза. Всего — 21 упоминание. Из новых акторов Аганбегян находится на 5-м месте по частоте упоминаний (связь "Осипов — Аганбегян" можно не учитывать ввиду ее малого веса). Дополнив же сеть самых сильных связей новой вершиной, мы получаем новую клику (подструктуру с повышенной сетевой плотностью) — ее фрагмент отображен на рис. 8. Условно ее можно обозначить артефактом "Новосибирская социологическая школа". Зная социальную историю российской социологии, можно сказать, что этот вывод тривиальный. В данном случае его можно расценивать как достаточно правдоподобный. Интересно, однако, установить и "неявные" группировки.
Заключение
Методика сетевого анализа основана на аппарате теории графов и может быть использована для изучения текстовых массивов, элементы которых связаны структурными соотношениями. Иначе говоря, это должны быть в некотором отношении связные тексты. В качестве "вершин", в принципе, могут быть определены любые концептуальные переменные [10]. Графические представления синтаксических и стилистических связей также можно отнести к сетям [11]. Особым видом ориентированных сетей являются генеалогические деревья, открывающие новую перспективу для анализа динамики социальной структуры [12]. Биографический материал особенно удобен для сетевого анализа тем, что в нем обнаруживаются своего рода сообщества персоналий, связанных контекстуальными переменными или артефактами. "Артефакты" — не самый удачный термин для обозначения контекстов, в которых репрезентируются сетевые связи, однако они порождаются связями и в этом смысле искусственны. В результате сетевого анализа текста возникает возможность его прочтения как палимпсеста, в том числе реконструкции "глубинных" структур, которые закрыты прагматическими и коммуникативными заданиями автора. Особой проблемой является обеспечение репрезентативности и надежности сетевых данных. Ошибки кодирования в текстах не являются систематическими и могут быть минимизированы повторными обращениями к массивам. Границы текста тоже не обязательно заданы началом и концом рассказа, и файлы могут быть объединены в одно коллективное повествование. Информанты не являются единицами исследования и не репрезентируют генсовокупность. Иное дело — соответствие рассказов реальности. Биографические нарративы принадлежат скорее жанру очерка, чем протокола. Для изучения коммуникаций в научном сообществе лучше всего использовать, например, дневники, записи телефонных разговоров, файлы электронной почты, но эти материалы доступны не всегда и не всем интересующимся. Приходится пользоваться теми документами, которые есть, и оценивать их качество на основе известных источниковедческих критериев.
В данной статье показаны фрагменты сетевого анализа профессионального сообщества социологов. Дальнейшая работа над методикой связана с расширением репертуара переменных. Уже сейчас достаточно отчетливо регистрируются "звезды", имеющие в сети высокий уровень центральности, положительный и отрицательный полюсы сети; а события, темы, институты, "школы" и другие артефакты не выходят за пределы историографических обзоров данного периода, хотя их совокупный объем несравнимо меньше объема обзоров [13]. В то же время в сетях необходимо формировать новые информативные переменные. В частности, не удалось зафиксировать "дисциплинарную консистентность" эгоцентрической и общей сетей. Речь идет об удельном весе несоциологов в профессиональной социологической "солидарности", то есть о степени дисциплинарной диффузности сетей. Проблема осложняется тем, что на данном материале невозможно более или менее уверенно отличить социолога от несоциолога. Социологом считается тот, кто называет себя социологом. В этом отношении общая сеть профессионального сообщества может показаться в высшей степени "чистой", хотя в числе артефактов редко встречаются указания на чисто научные проблемы, зато речь постоянно идет о проблемах власти, публичной политики, в том числе совершенствовании человека и общества. Не исключено, что расширение круга биографических документов и включение в информационный массив, скажем, менее влиятельных социологов позволит изменить картину распределения акторов и артефактов. По всей вероятности, историографический миф о российской социологии второй половины XX века будет соответствовать черно-белому изображению.
1 Вопрос о ценностных предпочтениях в сообществе социологов обсуждается в предисловии Г.С. Батыгина к рассматриваемой коллекции воспоминаний [3].
Список литературы
Knoke D. Associations and interest groups // Annual Review of Sociology. 1986. Vol. 12. P. 1-21.
Lin N. Social networks and status attainment // Annual Review of Sociology. 1999. Vol. 25. P. 467-487.
Российская социология шестидесятых годов в воспоминаниях и документах / Отв. ред. и автор предисл. Г.С. Батыгин; Ред.-сост. С.Ф. Ярмолюк. СПб.: Изд-во РХГИ, 1999.
Wasserman S., Faust K. Social network analysis. Cambridge: Cambridge University Press, 1994.
David M., Zeitlin D. What are they doing? Dillemas in analysing bibliographical searching: cultural and technical network in academic life // Sociological Research Online. 1998. No. 1, 4. <htpp://www.scoresomline/1/4/2.html>
Portes A. Social capital: Its origins and application in modern sociology. Princeton: Princeton University Press, 1998.
Бородкин Л.И. Многомерный статистический анализ в исторических исследованиях. М.: Изд-во Московского университета, 1986.
Голофаст В.Б. Многообразие биографических повествований // Социологический журнал. 1995. N 1
Freeman L.C. Centrality in social networks: conceptual clarifications // Social Networks. 1979. Vol. 1. P. 215-236.
Баранов А.В. Введение в прикладную лингвистику: Учебное пособие. М.: Эдиториал УРСС, 2001. С. 248.
Севбо И.П. Графическое представление стилистических структур и стилистическая диагностика. Киев: Наукова думка, 1981.
Божков О.Б. Родословные (генеалогические) деревья как объект социологического анализа // Социологический журнал. 1998. N 3/4.
Социология в России / Под ред. В.А. Ядова. М.: Изд-во Института социологии РАН, 1998.
11-09-2015, 00:39