Міністерство освіти і науки України
Національний транспортний університет
Кафедра проектування доріг
Методичні вказівки
Практичні рекомендації з дисципліни “інженерні вишукування”
Київ НТУ 2009
Інженерні вишукування – комплексна дисципліна, яка вивчає такі види інженерних вишукувань як економічні, екологічні, архітектурно – містобудівні, геодезичні, геологічні, гідрометричні, меліоративні, транспортні, розглядає соціальні, демографічні, історико–архітектурні вишукування тощо. Основною концепцією є визначення вишукувань як збору та систематизації інформації про стан середовища для майбутнього будівництва. Мета вивчення дисципліни полягає в отриманні знань про склад та методи проведення відповідних вишукувань, уміння аналізувати одержані результати, вирішувати практичні задачі.
На практичні заняття по курсу “Інженерні вишукування” виносяться задачі, пов’язані з економічними (тип І), транспортними (тип ІІ) та інженерно-геодезичними (тип ІІІ) вишукуваннями.
I. Тип 1
Задачі типу 1 розв`язуються на основі матеріалів економічних вишукувань. Завдання полягає у тому, щоб побудувати найкоротшу (оптимальну) пов’язуючи мережу, визначити додаткові вузлові точки та додаткові ланки
Вихідні дані :
1) розташування кореспондуючих точок ( рис. 1 )
2) матриця транспортних зв`язків ( табл. 1 )
4 О
О 2
6 О 3 О
5 О О 1
Рис. 1 План розташування кореспондуючих точок
Таблиця 1. Матриця транспортних зв`язків
| Кореспондуючі точки | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | Х | 19,0 - |
17,0 90 |
32,0 75,2 |
27,0 18,3 |
34,2 - |
| 2 | Х | 18,0 120,1 |
22,8 19,1 |
34,8 - |
33,2 35,0 |
|
| 3 | Х | 16,8 79,8 |
16,6 27,5 |
18,0 43,9 |
||
| 4 | Х | 26,4 - |
15,6 30,2 |
|||
| 5 | Х | 15,2 37,4 |
||||
| 6 | Х |
В чисельнику приведені відстані між кореспондуючими точками в км, в знаменнику – вантажонапруженість між цими точками , тис.т / рік .
Побудову найкоротшої по в’язучої мережі починають із кореспондуючої точки, яка має найінтенсивніші транспортні зв`язки: åQмах. Для цього визначають сумарний обсяг вантажних перевезень для кожної кореспондуючої точки і визначають ту, для якої він виявляється максимальним. Схема для визначення сумарних вантажних перевезень для кожного з кореспондуючих пунктів приведена в табл. 2.
Скажімо, для точки 3:
åQз = 90 + 120,1 + 79,8 + 27,5 + 43,9 = 361,3 (тис.т)
Для нашого прикладу
åQз = åQмах
В табл. 3 зведені результати попередніх підрахунків.
Таблиця 2. Схема визначення сумарних вантажних перевезень
| Кореспондуючі точки | 1 | 2 | 3 | 4 | 5 | 6 | åQ (тис.т) |
| 1 |
|
183,5 | |||||
| 2 |
|
174,2 | |||||
| 3 |
|
361,3 | |||||
| 4 |
|
||||||
| 5 |
|
83,2 | |||||
| 6 |
|
146,5 |
Таблиця 3. Сумарний обсяг вантажних перевезень
| Кореспондуючі точки | 1 | 2 | 3 | 4 | 5 | 6 | åQ (тис.т) |
| 1 | Х | 183,5 | |||||
| 2 | Х | 174,2 | |||||
| 3 | Х | 361,3 | |||||
| 4 | Х | ||||||
| 5 | Х | 83,2 | |||||
| 6 | Х | 146,5 |
åQмах. = åQ 3 = 361,3 тис.т.
До найкоротшої (оптимальної) пов’язуючої мережі відбирають ланки згідно із алгоритмом, де критерієм є мінімум питомих дорожньо-транспортних витрат, грн/т:
L = l [(aД / Q ) + bT], (1)
де l – довжина ланки, км;
а, b – коефіцієнти, які залежать від щорічного приросту вантажонапруженості та терміну перспективного проектування;
Д – дорожні витрати, пов`язані з будівництвом чи реконструкцією дороги, тис. грн / км;
Q – перспективна вантажонапруженість на ланці, тис. т.
Т – транспортна складова собівартості перевезень, грн / т.км.
Для спрощення розрахунків при відборі ланок до найкоротшої пов’язуючої мережі користуються показником мінімальної приведеної довжини. км / тис. т:
L = l / Q або L = l min / åQ, (2)
де l min – мінімальна довжина ланки, км;
åQ – сумарна вантажонапруженість на ланці, тис.т/ рік.
Відбір ланок до найкоротшої пов’язуючої мережі складаєтся з (n–1) циклів, кожен з яких полягає у визначенні приведених довжин, їх порівнянні та виборі найкоротшої ланки. Кожному циклу розрахунків надається шифр відповідно до номеру початкової кореспондуючої точки.
Якщо у вихідній мережі є дороги з твердим покриттям, їх автоматично включають до найкоротшої пов’язуючої мережі.
Перший цикл розрахунків починають з кореспондуючої точки, яка має найінтенсивніші транспортні зв`язки, тобто, з точки 3 ( табл.3 ). В таблиці 4 приведені обчислення для 3-ї точки - цикл 3 ( Ц-3 ). Значення відстаней між точкою 3 та іншими точками записані в рядку l, кількість вантажів, які перевозять – в рядку Q. За даними рядків l і Q визначають приведені довжини відстаней між точкою 3 та іншими кореспондуючими точками, які записують в рядок L. Аналіз рядка L показує, що мінімальна приведена довжина дорівнює 0,150 і відноситься до точки 2. Вона і приєднується, як найближча, до точки 3, утворюючи фрагмент найкоротшої пов`язуючої мережі (3-2). В наступних обчисленнях точки 3 і 2 вже не розглядаються.
Таблиця 4. Цикл обчислень Ц-3
| Ц-3 | 1 | 2 | 3 | 4 | 5 | 6 |
| l | 17,0 | 18,0 | X | 16,8 | 16,6 | 18,0 |
| Q | 90 | 120,1 | X | 79,8 | 27,5 | 43,9 |
| lmin | 17,0 | 18,0 | X | 16,8 | 16,6 | 18,0 |
| åQ | 90 | 120,1 | X | 79,8 | 27,5 | 43,9 |
| L | 0,189 | 0,150 | X | 0,210 | 0,603 | 0,410 |
| (3) | (3) | (3) | (3) | (3) |
В наступному циклі (табл. 5) визначається точка, яка є найближчою до визначеного фрагменту (3-2). Для цього необхідно визначити приведені довжини від інших кореспондуючих точок для фрагменту (3–2) - цикл 2 (Ц–2).
Рядки l та Q циклу Ц-2 заповнюються аналогічно табл.4. Рядок l min заповнюють, порівнюючи довжини від усіх кореспондуючих точок, ще не включених до мережі, до точок 3 і 2, які вже складають фрагмент мережі: записується менше значення. Наприклад: відстань від точки 2 до точки 1 складає 19,0 м , а від точки 3 до точки 1 – 17,0 м ( табл. 3). Тож в рядок l min циклу Ц–2 записуємо менше значення 17,0 м, яке відповідає відстані до точки 3, що фіксуємо в нижньому рядку - ставимо індекс (3). Індекс (3) вказує на те, що найкоротша відстань від точки 1 до фрагменту 3-2 визначається ланкою 3-1. Аналіз вантажних перевезень показує, що між точками 1 і 3 потрібно перемістити 90 тис. т, а між точками 1 і 2 вантажі не переміщуються (табл. 3). Отже, сума вантажів, які треба перемістити між точкою 1 і ланкою 3-2, складає 90 тис. т. Між точками 4 і 3 переміщується 79,8 тис. т.,між точками 4 і 2 - 19,1тис.т. Отже, сума вантажів, які підлягають переміщенню між ланкою 3-2 і точкою 4, складає 98,9 тис. т. Визначені значення записуються в рядок åQ.
На основі визначених найкоротших відстаней та сумарних обсягів перевезень визначаються приведені довжини, які записуються в рядок L.
Таблиця 5. Цикл обчислень Ц – 2.
| Ц - 2 | 1 | 2 | 3 | 4 | 5 | 6 |
| l | 19,0 | X | X | 22,8 | 34,8 | 33,2 |
| Q | - | X | X | 19,1 | - | 35,0 |
| l min | 17,0 | X | X | 16,8 | 16,6 | 18,0 |
| åQ | 90 | X | X | 98,8 | 27,5 | 78,9 |
| L | 0,189 | X | X | 0,170 | 0,603 | 0,228 |
| (3) | X | X | (3) | (3) | (3) |
В такій же послідовності розглядаються інші кореспондуючі точки
Обчислення, наведені в табл. 5, показують, що найменшою приведеною довжиною є L = 0,170, яка відноситься до точки 4. Отже, точка 4 приєднується до найкоротшої по в’язучої мережі, поєднуючись з точкою 3 (що зафіксовано в останньому рядку табл. 5) і в подальших обчисленнях не розглядається. Утворився наступний фрагмент мережі (2-3-4).
В таблицях 6, 7 та 8 наведені розрахунки для наступних циклів обчислень, які виконуються аналогічно до попередніх .
Таблиця 6. Цикл обчислень Ц – 4.
| Ц - 4 | 1 | 2 | 3 | 4 | 5 | 6 |
| l | 32,0 | X | X | X | 26,4 | 15,6 |
| Q | 75,2 | X | X | X | - | 30,2 |
| l min | 17,0 | X | X | X | 16,6 | 15,6 |
| åQ | 165,2 | X | X | X | 27,5 | 109,1 |
| L | 0,103 | X | X | X | 0,603 | 0,143 |
| (3) | X | X | X | (3) | (4) |
Таблиця 7. Цикл обчислень Ц –1
| Ц - 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| l | X | X | X | X | 27,0 | 34,2 |
| Q | X | X | X | X | 18,3 | - |
| l min | X | X | X | X | 16,6 | 15,6 |
| åQ | X | X | X | X | 45,8 | 109,1 |
| L | X | X | X | X | 0,363 | 0,143 |
| (3) | (4) |
Таблиця 8. Цикл обчислень Ц – 6.
| Ц - 6 | 1 | 2 | 3 | 4 | 5 | 6 |
| l | X | X | X | X | 15,2 | X |
| Q | X | X | X | X | 37,4 | X |
| l min | X | X | X | X | 15,2 | X |
| åQ | X | X | X | X | 83,2 | X |
| L | X | X | X | X | 0,182 | X |
| (6) |
В результаті проведених розрахунків отримані ланки найкоротшої пов’язуючої мережі (табл.9 ), яка показана на рис. 2.
Таблиця 9. Ланки найкоротшої (оптимальної) по в’язучої мережі
| № п/п | Шифр ланки |
| 1 | 3 – 2 |
| 2 | 3 – 4 |
| 3 | 3 – 1 |
| 4 | 4 – 6 |
| 5 | 6 – 5 |

 4 О
4 О
 О 2
О 2

![]() 6 О 3 О
6 О 3 О
5 О О 1
Рис. 2. Найкоротша ( оптимальна) пов’язуюча мережа
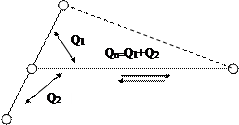
Після побудови найкоротшої (оптимальної) пов’язуючої мережі з`являється основа, яка дозволяє вирішувати питання про розміщення додаткових вузлових точок. Ланки найкоротшої пов’язуючої мережі зв`язують між собою кореспондуючі точки, в яких сходяться або перетинаються різні маршрути. Ці ж точки є вузлами поєднання окремих ланок мережі. Але на практиці виявляється доцільним влаштовувати примикання доріг і в інших точках, які звуться додатковими вузловими точками. Ознакою необхідності такої додаткової вузлової точки є наявність гострого кута, утвореного ланками мережі. Для того, щоб визначити додаткові вузлові точки, визначають кут примикання за формулою:
сos α = [(Q1 – Q2 ) Tосн ] / [Q n F ( Q n ) T під ] (3)
F( Q n ) = 1 + (a Д) / (Q n b T під ), (4)
де Q1 ,Q2 , - кількість вантажів, які підлягають переміщенню відповідно праворуч і ліворуч від примикання по головній ланці, тис. т.
Qn – кількість вантажів, які підлягають переміщенню по під`їзній ланці, тобто сума Q1 і Q2 , тис.т.
Тосн , Тпід – транспортна складова собівартості перевезень, відповідно по головній ланці та ланці, прийнятій під`їзною, грн./ Т км;
а та b – коефіцієнти, які враховують ефективність капіталовкладень, враховані в табл.10.
Для полегшення виконання обчислень за наведеними формулами складається таблиця 10.
Таблиця 10. Таблиця визначення аД та bТ
Категорія дороги |
Інтенсивність руху, N авт / добу |
Вантажонапруженість,Q , тис.т. | Дорожні витрати, приведені до звітного року, Д, у.о. / км | Транспортна складова собівартості перевезень, Т , у.о ./ т.км |
аД | вТ |
| 1 | > 10000 | 9893 | 1493 | 0,02 | 522,5 | 0,0406 |
| 2 | 10000 - 3000 | 9893 -2968 | 786 | 0,04 | 275 | 0,0812 |
| 3 | 3000-1000 | 2968 - 989 | 538 | 0,06 | 188,3 | 0,1218 |
| 4 | 1000-150 | 989 - 150 | 237 | 0,08 | 82,9 | 0,1624 |
| 5 | < 150 | 150 | 102 | 0,10 | 35,7 | 0,203 |
Вантажонапруженість підраховується за формулою:
Q = Nв Д Кп Кв Вср f, (5)
де Nв - кількість вантажних автомобілів транспортного потоку, авт / добу,
Д –кількість робочих днів на рік , Д = 320;
Кп – коефіцієнт використання пробігу автомобілями;
Кв - коефіцієнт використання вантажопідйомності автомобіля;
Вср – середня вантажопідйомність автомобілів,
Вср = (В1 Р1 + В2 Р2 + … Вn Pn ) / ( P1 + P2 +…+ Pn ), (6)
B 1 -…Bn – вантажопідйомність кожної марки автомобіля, т ;
P1 … Pn –відсоток автомобілів певної марки в потоці ; %;
f - коефіцієнт необлікованих перевезень , f = 1,1 – 1,2 .
Значення D та Т, наведені в табл. 10, прийняті відповідно до нормативних та статистичних даних (надалі при розрахунках використовуються дані табл.10).
Вантажонапруженість, відповідно до категорій доріг, визначають в наступній послідовності. Скажімо, для дороги I-ої категорії при інтенсивності N = 10000 авт/добу і 65 % вантажних автомобілів у транспортному потоці (згідно з завданням ), інтенсивність вантажного потоку :
![]()
Середня вантажопідйомність автомобілів відповідно до формули ( 6 ) :
Bср = ( 7 33 + 4 25 + 3,5 7 ) / ( 33 + 25 +7 ) = ( 231 +100 + 24,5 ) / 65 = 5,47 т
Вантажонапруженість розраховується за формулою ( 5 ) :
QI = 6500 × 320 × 0,85 × 0,93 × 5,47 × 1,1 = 9893392 т
Для II категорії :
![]()
QII = 1950 × 320 × 0,85 × 0,93 × 5,47 × 1,1 =2968018 т
Для III категорії :
![]()
QIII = 650 × 320 × 0,85 × 0,93 × 5,47 × 1,1 =989339 т
Для IV , V категорій :
![]()
Q= 98 × 320 × 0,85 × 0,93 × 5,47 × 1,1 =149162 т
Відповідні значення Q заносяться в табл.10.
Додаткові вузлові точки слід шукати в тих випадках, коли ланки, які сходяться в кореспондуючій точці, утворюють гострий кут. Ця обставина є зовнішньою ознакою, яка умовно полегшує пошук вузлових точок.
На рис.3 показане можливе розташування вузлової точки 7, якщо вантажі переміщуватимуться з точки 3 в точку 6 за маршрутом 3-7, 7-6, а не 3-4, 4-6
 4
4
7 3
6
Рис. 3. Схема до визначення положення вузлової точки
Відповідно до рис.3, праворуч від точки примикання 7 будуть переміщуватися вантажі :
Q1 = Q3-4 + Q2-4 + Q1-4 = 79,8 + 19,1 +15,2 =174,1 тис. т
Ліворуч від точки 7 будуть переміщуватися вантажі :
Q2 = Q3-6 +Q2-6 +Q1-6 +Q3-5 +Q2-5 +Q1-5 =43,9+35,0+0+27,5+0+18,3=124,7 тис. т
Qn = Q1 +Q2 = 174,1 + 124,7 = 298,8 тис. т.
За даними табл.10 Q n відповідає вантажонапруженості для дороги 4-ої категорії, відповідно для 4-ої категорії приймаються за даними табл.10 і значення аD і bT , які потрібні для розрахунків.
Тоді за формулою (4) :
F (Qn
) = 1 + ![]()
Обчислюємо значення кута примикання a ( формула 3 ) :
cos a = [| 174,1 – 124,7 | 0,10 ] / ( 298,8 2,71 0,08 ) = 0,075 ;
a = 85 o 42` .
Значення Тосн та Тпід в формулі ( 3 ) беруться із табл.10 відповідно до різниці | Q1 - Q2 | , якій відповідає Тосн = 0,10 для 5-ої категорії дороги, та зна-чення Qn, якому відповідає Тосн = 0,08 для 4-ої категорії дороги. Кут a відкладається між ланками (3-4) та (4-6) простою побудовою. Своєю вершиною кут a направляється в сторону більшого вантажопотоку. Ланка (4-6) механічно ділиться на дві ланки : (4-7) та (7- 6 ), довжина яких визначається за масштабом і, відповідно, складає 5,0 км та 10,6 км. Отже, замість ланки (3-4) утворилася нова ланка (3-7) завдовжки 15,8 км.
Для визначення необхідності додаткових ланок виконують перевірку :
lф
/ li-j
>
<
![]() [ 1+
[ 1+ ![]() ] , (7)
] , (7)![]()
де lф , li-j - довжина відповідного маршруту за ланками найкоротшої пов’язуючої мережі та довжина додаткової ланки, км;
Q – кількість вантажів, які необхідно перевезти між точками, тис. м;
Кпр – коефіцієнт прискорення перевезень, Кпр = 0,7 – 0,8.
Якщо ліва частина нерівності є більшою за праву – додаткова ланка приймається, якщо ні – в ній немає необхідності. Можливі додаткові ланки для побудованої найкоротшої пов’язуючої мережі вказані на рис. 4.
 4
4
7 2
6
3
5 1
Рис. 4. Схема мережі із можливими додатковими ланками.
Необхідність введення додаткових ланок розглядається для кожного окремого незамкненого контуру найкоротшої пов’язучої мережі. Розглянемо додаткову ланку між точками 3 та 6, відстань між якими 18,0 км, а вантажонапруженість 43,9 тис. т. При відсутності дороги між точками 3 та 6 вантажі між ними слід перевозити по ланках 3-7 і 7-6, довжиною відповідно 15,8 км та 10,6 км , тобто довжина маршруту за ланками найкоротшої пов’язучої мережі : lср =15,8км + 10,6км = 26,4км.
Тоді ліва частина нерівності (7):
lф / l3-6 = 26,4 / 18 =1,46 ;
Права частина нерівності (7):
![]()
Оскільки 1,46 < 2,79 , то додаткової ланки влаштовувати не потрібно.
Розглянемо додаткову ланку між точками 3 та 5 , відстань між якими l 3-5 = 16,6км , а вантажонапруженість 27,5т. За відсутності дороги між точками 3 та 5 вантажі між ними будуть перевозитися за маршрутом 3-7, 7-6, 6-5, довжиною lф = 15,8км + 10,6км + 15,2км = 41,6 км.
Ліва частина нерівності (7) : lф / l3-5 = 41,6 / 16,6 =2,50 ;
права частина нерівності (7) :
![]()
Оскільки 2,50 < 3,37 , то додаткова ланка не потрібна.
Розглянемо додаткову ланку між точками 1 та 5 , відстань між якими l1-5 = 27,0км , а вантажонапруженість 18,3тис.т. За відсутності дороги вантажі слід перевозити за маршрутом 1-3 , 3-7 , 7-6 , 6-5 , довжина якого lф = 17,0км + 15,8км + 10,6км + 15,2км = 58,6 км.
58,6 / 27,0![]()
![]() [ 1+
[ 1+ ![]() ] ;
] ;
2,17 < 4 , отже додаткової ланки влаштовувати не потрібно.
Розглянемо додаткову ланку 2-4 , l2-4 = 22,8км ; вантажонапруженість 19,1 тис. т.
lф = l2-3 + l3-7 + l7-4 = 18,0км + 15,8км + 5,0км = 38,8км
38,8 / 22,8![]()
![]() [ 1+
[ 1+ ![]() ] ;
] ;
1,7 < 3,83, додаткова ланка не потрібна.
Остаточний вигляд дорожньої мережі приведений на рис.5
Додаткова ланка 1-2 не розглядається, оскільки по ній не здійснюються перевезення (табл. 1).
 4
4
7 2
6
3
5 1
Рис.5. Остаточний вигляд раціональної дорожньої мережі.
II. Тип 2.
Задачі типу 2 – це задачі, які виникають при обробці даних та аналізі результатів транспортних вишукувань, а саме – вимірювання миттєвих швидкостей. Результати визначення миттєвих швидкостей записуються у вигляді таблиці 11. Завдання полягає у визначенні швидкостей 15% , 50% та 85% забезпеченості.
Таблиця 11. Розподіл миттєвих швидкостей руху
Види транспортних засобів (ТЗ) |
Швидкості руху , км / г | Всього ТЗ |
|||||||||||||
15 20 |
20 25 |
25 30 |
30 35 |
35 40 |
40 45 |
45 50 |
50 55 |
55 60 |
60 65 |
65 70 |
70 75 |
75 80 |
80 85 |
||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Легкові авт. | 5 | 7 | 9 | 10 | 15 | 20 | 18 | 20 | 16 | 17 | 10 | 7 | 5 | 2 | 161 |
| Вантажні авт | 2 | 8 | 10 | 7 | 8 | 5 | 3 | 3 | 2 | 2 | 1 | - | - | - | 51 |
| Автопоїзди | 2 | 2 | 1 | 2 | 3 | 2 | 1 | - | - | - | - | - | - | - | 13 |
| Автобуси | 1 | 2 | 3 | 4 | 5 | 7 | 8 | 5 | 1 | - | - | - | - | - | 36 |
| Мотоцикли | - | 1 | 1 | 1 | - | - | - | - | - | - | - | - | - | - | 3 |
| Транспортний потік, авт. | 10 | 20 | 24 | 24 | 31 | 34 | 30 | 28 | 19 | 19 | 11 | 7 | 5 | 2 | 264 |
| Частість,% | 4 | 8 | 9 | 9 | 12 | 13 | 11 | 10 | 7 | 7 | 4 | 3 | 2 | 1 | 100 |
Підраховуються кількість автомобілів кожного виду (стовпчик 16), кількість та відсоток автомобілів, які рухаються в
29-04-2015, 01:07
