Механічний рух тіл. Основна задача механіки та її розв’язання
Фізичне тіло і матеріальна точка. Система відліку
Відносність механічного руху
Векторні і скалярні величини. Дії над векторами
Траєкторія руху. Шлях і переміщення
Рівномірний прямолінійний рух. Швидкість руху тіла
Закон додавання швидкостей
Графічне зображення рівномірного прямолінійного руху
Рівноприскорений прямолінійний рух тіла. Прискорення руху тіла
Графічне зображення рівноприскореного руху
Вільне падіння тіл. Прискорення вільного падіння
МЕХАНІЧНИЙ РУХ ТІЛ. ОСНОВНА
ЗАДАЧА МЕХАНІКИ ТА ЇЇ РОЗВ’ЯЗАННЯ
Фізика розглядає різноманітні природні явища, з якими ви вже ознайо милися раніше, в основній школі: механічні, теплові, електричні, оптичні. У профільній школі будемо вивчати їх детальніше, враховуючи вже набуті вами знання з фізики і математики. Розпочнемо з розгляду механічного руху як одного з найважливіших для практики і найпростіших для спри йняття фізичних явищ.
Усі тіла навколо нас у будьякий момент часу мають певне розташуван ня у просторі. Якщо з часом положення тіл змінюються, то кажуть, що тіла рухаються.
Механічний рух — це зміна з часом взаємного положення у просторі ма теріальних тіл або взаємного положення частин даного тіла.
Розділ фізики, в якому пояснюється механічний рух матеріальних тіл, а також взаємодії, які відбуваються при цьому між тілами, називають механікою.
Термін «механіка» вперше ввів Арістотель, що в перекладі з грецької означає машина або пристрій .
Щоб вивчити рух тіла, треба дослідити, як змінюється його положення у просторі з часом, тобто вміти визначати його координати у будьякий мо мент. Так, астрономи, знаючи закони руху небесних тіл, можуть розраху вати з великою точністю, наприклад, появу в певний момент у певній ділянці неба комети.
Основна задача механіки полягає у визначенні положення тіла у будьякий момент часу.
Така задача має єдиний розв’язок тільки за конкретних початкових умов, тобто коли відоме початкове положення (координати) тіла і початко ва швидкість його руху. Розв’язок основної задачі механіки математично подається у вигляді певної функції (залежності) координат тіла від часу.
У цьому розділі ми будемо досліджувати тільки просторові (геомет ричні) характеристики механічного руху тіла, його траєкторію, координа ти та швидкість, не враховуючи масу тіла та причини, які змінюють стан його руху.
Розділ механіки, в якому вивчають рухи матеріальних тіл без урахування мас цих тіл і сил, що на них діють, називають кінематикою.
Отже, щоб розв’язати основну задачу механіки, насамперед треба з’ясу вати, які існують різновиди руху та їх характеристики.
1. Що таке механічний рух?
2. Сформулюйте завдання механіки як розділу фізики.
3. У чому полягає основна задача механіки та розв’язання її в кінематиці?
4. Що вивчає кінематика?
ФІЗИЧНЕ ТІЛО І МАТЕРІАЛЬНА ТОЧКА.
ПОСТУПАЛЬНИЙ РУХ. СИСТЕМА ВІДЛІКУ
Під час дослідження руху якогось тіла постає завдання визначати його положення у просторі у певні моменти часу. Наприклад, ми хочемо описа ти рух каменя, який кинули у річку. Камінь має певні розміри і форму, складається з величезної кількості атомів, під час польоту він безладно об ертається, окремі його точки рухаються порізному. Щоб описати детально рух такого тіла, треба дослідити рух усіх його частинок — це настільки складна задача, що на її розв’язання не вистачить обчислювальних потуж ностей і часу.
Проте у фізиці часто задачу, залежно від її умов, можна розв’язати на ближено й отримати цілком задовільний результат. Для цього замість ре ального тіла розглядають його спрощену ідеальну модель , тобто об’єкт, у якому нехтують несуттєвими для даної задачі властивостями заданого тіла, залишаючи лише його основні, визначальні риси.
Якщо камінь у наведеному прикладі до падіння у воду подолав відстань, значно більшу за його розміри, то вони не будуть суттєво впливати на ха рактер його руху й у граничному випадку тіло можна вважати точкою.
Крім того, на рух тіла не впливають його атомна структура, теплові, електричні, оптичні властивості тощо. Для опису у спрощеній моделі руху тіла, а пізніше і причин цього руху, досить, щоб геометрична точ ка мала масу, що дорівнює масі да ного тіла, і могла рухатись. Таку ідеальну модель реального тіла на зивають матеріальною точкою
.
Матеріальною точкою є тіло, розмірами якого за даних умов руху можна знехтувати.
У наведеному визначенні дуже важливі слова «за даних умов руху», які виражають обмеженість застосування даного поняття. Ма теріальна точка — поняття від носне, а не абсолютне. Одне й те саме тіло в одній задачі можна роз глядати як матеріальну точку (рух космічного корабля на орбіті, рух океанського лайнера, які є малими порівняно з протяжністю шляхів, що вони долають), а в іншій — як тіло скінченних розмірів і певної форми (стикування одного косміч ного корабля з іншим). У більшості випадків далі у нашому курсі вва жатимемо рухомі тіла матеріальни ми точками. Зрозуміло, що задача опису механічного руху тіл дуже спроститься.
У наведених вище прикладах усі точки рухомого тіла рухалися порізному. Але на практиці дуже часто тіла рухаються так, що всі їх точки рухаються однаково. Одна ково рухаються точки кузова авто мобіля на прямій ділянці дороги, різця токарного верстата, вантажу на канаті підіймального крана (мал. 1, а ), кабінок колеса огляду (мал. 1, б ), поршня у циліндрі дви гуна автомобіля, шухляди, що ви тягують зі столу, санчат, що опускаються з гори, голки швейної машини, ручки під час писання
(мал. 1, в ) тощо.
Рух тіла, під час якого всі його точки рухаються однаково, називають посту/ пальним.
Коли тіло рухається поступально, будьякий виділений напрям у тілі, наприклад пряма вздовж планки висувної шухляди, залишається пара
лельним своєму положенню у будьякий момент часу. Іншими словами, тіло при поступальному русі не обертається. Зрозуміло, що під час дослідження поступальних рухів досить описати рух лише однієї точки тіла, що також значно спрощує розв’язання основної задачі механіки.
Місцезнаходження досліджуваного тіла під час руху можна визначити, вказавши його розташування відносно іншого тіла.
Тіло, відносно якого визначають положення інших тіл у різні моменти часу, нази вають тілом відліку.
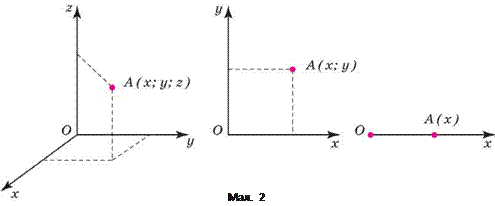
Для визначення положення тіла відносно тіла відліку математично ко ристуються певною системою координат. За початок декартової системи координат беруть довільну точку тіла відліку, з якою жорстко пов’язують осі системи. Користуючись одиничним масштабом, можна визначити коор динати х , у , z будьякої точки простору, відкладаючи масштаб у напрямі координатних осей. Положення кожної точки у просторі визначається трьома координатами, на площині — двома, на прямій — однією (мал. 2).
Якщо точка рухається відносно тіла відліку, то потрібно знати не тільки де, а й коли вона перебуває у відповідному місці. Отже, для одержання повної інформації про рух тіла (точки), треба вміти вимірювати час. Час вимірюють, використовуючи якийнебудь перебіг рівномірного періодично го процесу, наприклад хід годинника.
Тіло відліку, з яким пов’язана система координат, і годинник для вимірювання часу утворюють сисему відліку.
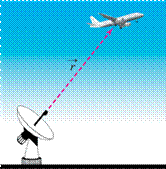Наведемо приклад системи відліку, яка відрізняється від описаної вище. Щоб виявити місцезнаходження літака, радіолокатор поси лає сигнал і через час t
приймає відбитий сиг нал (мал. 3). Відстань до літака обчислюється t
8
за формулою l
c
, де с
3 · 10 м/с — стала
2
швидкість сигналу.
Місцезнаходження літака відносно радіоло катора у цьому разі визначається також трьома координатами: відстанню до літака l і двома ку тами, які визначають за розташуванням антени під час вимірювань, — кутом азимуту напряму Мал. 3 на літак відносно напряму на північ і кутом між горизонталлю та напря мом на літак.
Під час руху положення тіла змінюється відносно системи координат, тобто з часом змінюються і значення координат певної точки тіла. Розгля немо, як у фізиці визначають зміну фізичної величини з часом. Напри клад, координати точки, відлічені вздовж осей координат у момент часу, який прийняли за початковий (t 0 0), дорівнювали відповідно x 0 , y 0 , z 0 . Через певний інтервал часу t – t 0 (або просто t , оскільки t 0 0) вони зміни лися і набули значень x, y, z . Це означає, що за час t координата x змінила ся на (x – x 0 ), координата y — на (y – y 0 ), координата z — на (z – z 0 ). Кожна з різниць x – x 0 , y – y 0 , z – z 0 є також фізичною величиною — зміною коор динат x , y , z за відповідний інтервал (зміну) часу t – t 0 . Щоб визначити зміну будь,якої фізичної величини, треба від її кінцевого значення відня, ти її початкове значення.
Часто застосовують скорочений запис зміни фізичної величини за допо могою знака (грецька літера дельта), який пишуть перед позначенням змінюваної фізичної величини, наприклад: x x – x 0 , y y – y 0 , z z – z 0 , t = t – t 0 .
1. З якою метою в механіці користуються ідеальними моделями?
2. Що розуміють під матеріальною точкою? Чи можна сказати, що це просто дужемаленьке тіло?
3. У яких випадках застосовують поняття матеріальної точки?
4. Назвіть ознаки поступального руху.
5. Коли в механіці під час дослідження руху можна обмежитись описом руху однієїточки?
6. Чим розрізняються між собою тіло відліку і система відліку?
7. Що таке зміна фізичної величини? Як її визначають?
ВІДНОСНІСТЬ МЕХАНІЧНОГО РУХУ
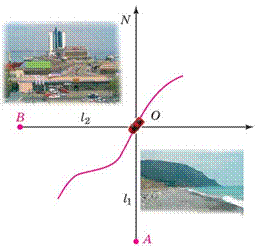
Досліджуючи механічний рух, тіло відліку можна вибирати довільно, але звичайно його вибирають з міркувань зручності, щоб опис руху мав на йпростіший вигляд. Зокрема, можна розглядати кілька різних тіл, з кож ним з яких пов’язана своя система прямокутних координат з довільним орієнтуванням осей. Це дає можливість одночасно розглядати положення одного тіла в різних системах координат. Зрозуміло, що в різних системах координат положення того самого тіла може бути зовсім різним. Напри клад, положення автомобіля на шляху можна визначити, зазначивши, що він перебуває на відстані l 1 на північ від населеного пункту А (мал. 4). Вод ночас можна сказати, що автомобіль перебуває на відстані l 2 на схід від пункту В . Це означає, що положення тіла відносне: воно різне відносно різних тіл відліку і пов’язаних з ними систем координат.
З відносності положення тіла випливає також відносність будь,якого механічного руху. У чому ж вона полягає?
Вибране тіло буде рухатись порізному відносно інших тіл: людина, яка їде в потязі, відносно Землі рухається, а відносно вагону потяга пе ребуває у стані спокою. Літаки, що летять групою, перебувають один відносно одного у стані спо кою, відносно Землі рухаються з великою швидкістю, наприклад км
900 , а відносно такої ж групи год
літаків, що рухаються у зворот ному напрямі, вони рухаються зі км швидкістю 1800 .
год
Будьякий механічний рух і, зокре ма, стан спокою тіла є відносними.
Відповідаючи на запитання, рухається тіло чи перебуває у стані спокою, необхідно вказати, відносно яких тіл розглядається
Мал. 4 рух цього тіла. Безглуздо і немож ливо розглядати якийсь «абсолютний рух» тіла або «рух взагалі» безвідносно до певного тіла відліку.
1. У чому полягає відносність механічного руху?
2. Як визначити, рухається тіло чи перебуває у стані спокою?
3. Поясніть, хто перебуває в русі: пасажир, який їде в автобусі, чи людина, щостоїть на автобусній зупинці?
4. Що насправді рухається: Земля навколо Сонця чи Сонце навколо Землі?
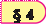ВЕКТОРНІ І СКАЛЯРНІ ВЕЛИЧИНИ. ДІЇ НАД ВЕКТОРАМИ
Фізичні величини, що характеризують фізичну систему і її стани (на приклад взаємодію і механічний рух тіл) відображаються відповідними ма тематичними об’єктами. Наприклад, щоб задати масу, температуру, об’єм тіла, треба визначити тільки їх числові значення у певних одиницях. Щоб задати силу або швидкість, треба обов’язково знати, крім числового значен ня, ще і їхній напрям у просторі, від чого залежить перебіг самого явища.
Фізичні величини, які виражають тільки числом, називають скалярними , або скалярами.
Математичні дії зі скалярними величинами визначаються відомими вам правилами арифметики.
Фізичні величини, які характеризують числовим значенням, напрямом і геомет ричним способом додавання, називають векторними , або векторами.
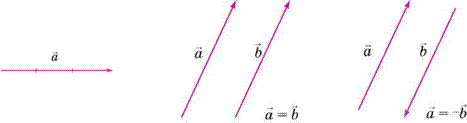
Числове значення вектора називають модулем вектора. Модуль векто ра — величина скалярна и додатна. Векторну фізичну величину зобража ють стрілкою, довжина якої у вибраному масштабі дорівнює модулю вектора, а напрям збігається з напрямом фізичної величини (мал. 5). Якщо модуль вектора дорівнює нулю, то вектор зображається точкою.
Мал. 5 Мал. 6 Мал. 7
Позначають вектори напівжирними літерами, наприклад a , b , c , або світлими літерами зі стрілками над ними: a , b , c .
Модуль вектора позначають або за допомогою математичного знака мо
дуля | a |, | b |, | c |, або просто світлими літерами a , b , c . Надалі будемо корис туватися цим останнім позначенням модуля вектора.
Вектори a і b є рівними, якщо вони мають однакові модулі і напрями (мал. 6). Вектори можна множити на скаляр, якщо помножити вектор a на скаляр k , то отримаємо вектор добутку p такого самого напряму, як у век тора a , з модулем, що дорівнює добутку модуля вектора a на модуль скаля ра k : p ka . Якщо вектор a помножити на (–1), то його модуль залишиться
таким самим, а напрям зміниться на протилежний. Якщо вектори a і b рівні за модулем і мають протилежні напрями, то їх називають протилеж,
ними і пишуть a b (мал. 7).
Математичні вектори можна переносити паралельно самим собі, з фізич ними векторами це можна робити не завжди (наприклад, у задачах на рівно вагу, коли дія важеля залежить від точки прикладання вектора сили).
Вектори можна додавати за правилами геометричного , або векторно
го , додавання . Якщо додати вектори a і b , то отримаємо вектор їхньої
суми c , таку дію записують у вигляді векторної рівності: a b c . Щоб виз начити напрям і довжину (модуль) вектора суми c користуються такими правилами.
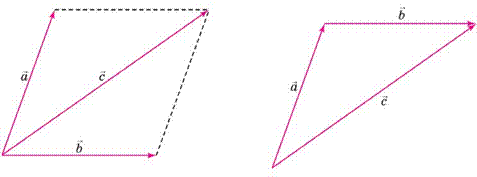
Правило паралелограма . Якщо вектори a і b мають спільний початок, то для їх додавання треба побудувати на цих векторах (як на сторонах) па
ралелограм (мал. 8), діагональ якого буде вектором суми векторів a і b .
Якщо в цьому паралелограмі від кінця вектора a до кінця вектора b провес
ти другу діагональ, то вона дорівнюватиме вектору різниці векторів a – b (перевірте це для вправи).
Мал. 8 Мал. 9
Мал. 10
Якщо вектори a і b не мають спільного початку, то їх можна за допомо гою паралельного перенесення привести до спільного початку.
Правило трикутника . Паралельним перенесенням вектора b сумістити його початок з кінцем вектора a , тоді вектором суми c a b буде вектор,
що з’єднує початок вектора a і кінець вектора b (мал. 9). Правило трикут ника еквівалентне правилу паралелограма, але його зручно застосовувати, коли треба додавати декілька векторів. Також за цим правилом неважко
отримати різницю векторів c a b . Перепишемо цю рівність у вигляді
c a ( b ), бачимо, що віднімання вектора еквівалентне додаванню проти
лежного йому вектора (–b ), що неважко зробити.
Коли вектори напрямлені вздовж однієї прямої або паралельні, їх нази вають колінеарними . Колінеарні вектори можуть бути напрямлені в один бік або в протилежні боки. Ви стикалися з обома випадками у 8 класі, коли визначали рівнодійну сил, прикладених до тіла, які діяли вздовж однієї прямої (мал. 10, а , б ).
Колінеарні вектори додаються так само, як і неколінеарні
, які ми роз глядали вище. Задача у цьому разі значно спрощується,
9-09-2015, 17:29