результат вам доб ре відомий: за модулем результуючий вектор дорівнює або арифметичній сумі (коли вектори напрямлені в один бік), або арифметичній різниці (коли вектори напрямлені протилежно) модулей векторів, що додаються. Результуючий вектор у першому випадку так само напрямлений, як і складові, у другому — у бік більшого за модулем вектора.

Рівняння механіки, як побачимо далі, мають зручну і наочну векторну форму, але під час обчислень ми оперуємо числами (скалярами), тому під час розв’язання задач виникає потреба перейти від векторного до скаляр ного запису. Для цього ознайомимося з поняттям проекції вектора на коор динатну вісь і правилами дій з проекціями векторів.

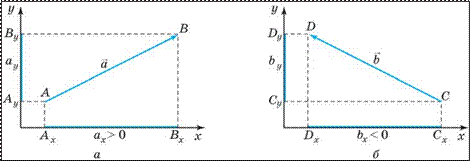
Мал. 11

Вам добре відомо з геометрії поняття проекції точки на пряму (вісь).

Проекцією точки на пряму (вісь) називають основу перпендикуляра, опущено го з цієї точки на пряму.

Зрозуміло, що оскільки відрізок складається з послідовної і безперерв ної сукупності точок, то проекція відрізка на вісь складатиметься з про екцій усіх його точок на цю вісь, це буде відрізок на осі, обмежений про, екціями початку і кінця даного відрізка .

На мал. 11, а, б зображені векториa і b , що порізному орієнтовані віднос но осей координат. Проекції точок і відрізків позначаються їхніми символа ми з нижнім індексом осі, проекція на яку розглядається. Наприклад, A_x , C_x — проекції початків векторів a і b на вісь Ох ; B_y , D_y — проекції кінців век торівa іb на вісь Oy . Визначаючи проекцію вектора на вісь, треба враховува ти, що знак проекції залежатиме від орієнтації цього вектора відносно осі.

Проекцію вектора на вибрану вісь вважають додатною, якщо від проекції по чатку вектора до проекції його кінця треба рухатися у напрямі цієї осі.

Проекцію вектора н а вибрану вісь вважають від’ємною, якщо від проекції по чатку вектора до проекції його кінця треба рухатися у напрямі, протилежному напряму цієї осі.

Відповідно до цих правил, проекція вектора a на вісь Ох буде додатною,

тобто a_x > 0, а проекція вектора b на вісь Oy — від’ємною, тобто b_x < 0.

Обидві проекції цих векторів на вісь будуть додатними, тобто a_x , b_x > 0.

Якщо відомі проекції кількох векторів на певну вісь, то, користуючись наведеними правилами і правилами додавання векторів, неважко визначи ти проекцію суми векторів на цю вісь.

Проекція вектора суми векторів на певну вісь дорівнює сумі проекцій век/ торів/доданків на цю вісь.

Якщо c a a , то c_x a_x + b_x , і c_y a_y + b_y . Перевірте це самостійно.

Ви бачите, що на площині векторному рівнянню відповідають два ска лярних рівняння. Значення проекцій векторів залежать від їх розташуван ня відносно системи координат, тому під час розв’язання задач намагаються вибирати напрями координатних осей таким чином, щоб спростити математичні перетворення й обчислення.

На мал. 12 показано різні випадки орієнтації вектора швидкості тіла v відносно осей координат. У загальному випадку вектор v напрямлений під кутом до осі Ох (мал. 12, в ) і його проекції визначатимуться за формула ми тригонометрії: v_x v cos і v_y v sin . Якщо вектор v напрямлений па ралельно осі Ох , то, як видно з мал. 12, а , модулі вектора і його проекції збігаються. При перпендикулярному розташуванні вектора v відносно осі

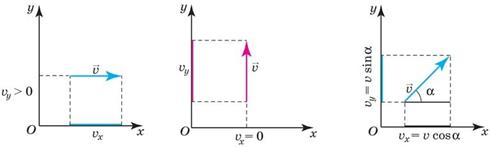
Мал. 12

Ох (мал. 12, б ) проекції його початку і кінця на цю вісь збігаються і модуль проекції дорівнює нулю.

1. Чим відрізняються векторні величини від скалярних?

2. Наведіть приклади векторних і скалярних величин.

3. За якими правилами додаються вектори?

4. Як знаходяться проекції векторів на координатні осі?

Р о з в’ я з у є м о р а з о м

1. В яких з наведених нижче прикладів досліджуване тіло можна вва жати матеріальною точкою: а) обчислюють тиск трактора на ґрунт; б) ви значають висоту підйому ракети; в) розраховують роботу, виконану під час піднімання залізобетонної плити перекриття відомої маси на задану висо ту; г) обчислюють масу сталевої кульки, користуючись мензуркою? В і д п о в і д ь: у випадках «б» і «в».

2. Коли літак летить над хмарами, то пасажирам іноді здається, щолітак падає вниз на хмари, чого насправді немає. Чим це пояснити?

В і д п о в і д ь: насправді хмари внаслідок конвекції піднімаються вгору і здається, ніби літак падає вниз.

Рівень А

1. Які рухи є рівномірними, а які — нерівномірними: а) рух літака назльоті; б) спускання на ескалаторі метрополітену; в) рух потяга при на ближенні до станції?

2. Яким буде рух колеса автомобіля, коли за ним спостерігатиме людина,що сидить у цьому автомобілі біля вікна?

3. Наведіть приклади задач, у яких Місяць:

а) можна вважати матеріальною точкою; б) не можна вважати матеріальною точкою.

4. Чи можна вважати Землю матеріальною точ кою, визначаючи: а) відстань від Землі до Сон ця; б) шлях, пройдений Землею по орбіті навколо Сонця за місяць; в) довжину екватора; г) швидкість руху точки екватора під час добо вого обертання Землі навколо осі; ґ) швидкість руху Землі по орбіті навколо Сонця?

5. Чи може людина, яка перебуває на рухомомуескалаторі, бути в стані спокою у системі відліку, пов’язаній із Землею?

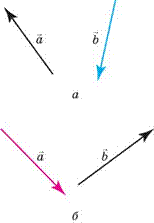
6. Додайте вектори за правилами трикутника і па ралелограма (мал. 13, а , б ).

Мал. 13

7. Велосипедист, що рухається по дорозі, крутить педалі. Який при цьомурух педалей — поступальний чи обертальний?

8. Чи можна вважати матеріальною точкою снаряд під час розрахунку:

а) дальності польоту снаряда; б) форми снаряда, яка забезпечує змен шення опору повітря?

9. Чи можна вважати матеріальною точкою залізничний потяг довжиноюприблизно 1 км під час розрахунку шляху, пройденого за кілька секунд?

10. Чому в літаку під час польоту, дивлячись в ілюмінатор на безхмарненебо, ми не відчуваємо, що літак летить? м

11. Швидкість штормового вітру 30 , а швидкість руху автомобіля дося

с

км

гає 150 . Чи може автомобіль рухатися так, щоб перебувати у спокої

год відносно повітря?

км м

12. Швидкість руху велосипедиста 36 , а швидкість вітру 4 . Яку год с

швидкість має вітер у системі відліку, пов’язаній з велосипедистом, коли: а) вітер зустрічний; б) вітер попутний?

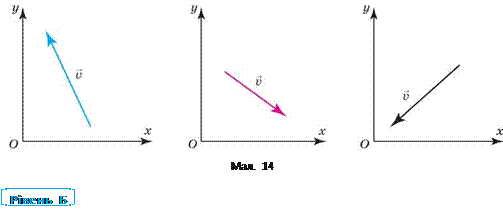
13. Знайдіть проекції векторів на координатні осі (мал. 14).

ТРАЄКТОРІЯ РУХУ. ШЛЯХ І ПЕРЕМІЩЕННЯ

Матеріальна точка під час механічного руху з часом послідовно змінює своє положення у просторі, кожному з яких відповідають значення коор динат у заданій системі відліку. Неперервна сукупність точок, що визнача ються цими координатами, утворює у просторі уявну лініютраєкторію, вздовж якої рухалося тіло.

Траєкторією руху точки називається уявна лінія, яку описує тіло під час руху.

Траєкторія — це слід, який залишає тіло під час свого руху, найчастіше — невидимий, інколи — видимий (слід від велосипедних коліс на сухому асфальті після подолання калюжі), інколи — заздалегідь заданий (залізничні або трамвайні рейки). За формою траєкторії механічні рухи бу вають прямолінійними (траєкторія — пряма лінія) і криволінійними , коли тіло рухається вздовж довільної кривої (мал. 15). За траєкторією легко

Мал. 15

визначити шлях , пройдений тілом під час руху, — досить виміряти довжи ну траєкторії.

Шлях — це довжина траєкторії, яку описало рухоме тіло (матеріальна точка) за певний інтервал часу.

Шлях є скалярною фізичною величиною, оскільки не має визначеного напряму і характеризується лише значенням. Шлях позначають латин ською літерою l . Одиницею шляху в СІ є один метр (1 м) .

На практиці знання шляху, який пройшло рухоме тіло, дає змогу ви значити, наприклад, час і кількість пального, що потрібні для його подо лання, але цього не досить для визначення положення тіла наприкінці руху. Отже, це можна зробити, якщо знати напрями, у яких перебувало тіло на початку і наприкінці руху, а також відстані до нього від тіла відліку в ці моменти. Знаємо, що число і напрям характеризують вектор, отже, ми прийшли до доцільності векторного опису механічного руху. Пе реваги такого опису полягають в його математичній наочності, крім того, такий спосіб задання положення тіла не залежить від орієнтації системи координат у просторі.

На мал. 16 точка А з координатами x , y відповідає положенню рухомої матеріальної точки на площині, а напрямлений відрізок r , що з’єднує по чаток координат і точку А , визначає відстань матеріальної точки від тіла відліку і напрям на неї.

Вектор, проведений з початку системи відліку в дану точку, називають радіус/вектором цієї точки.

Такий векторний спосіб задання місцеположення точки у просторі відповідає наведеному раніше прикладу про визначення положення літака радіолокатором (мал. 3).

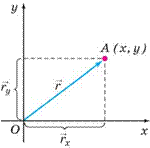Якщо з кінця радіусвектора опустити перпен дикуляри на осі координат, то можна визначити проекції радіусвектора r на ці осі: r_x — проекція радіусвектора r на вісь Ох , r_y — проекція радіусвектора r на вісь Оy . На мал. 16 добре вид но, що знайдені проекції збігаються з координата ми точки А :

r_x x , r_y y .

Якщо точка А рухається певною траєкторією, то довжина і напрям вектора r будуть відповідно

Мал. 16

змінюватися. На мал. 17 r ₀ — це радіусвектор матеріальної точки в початковий момент руху, а r — радіусвектор цієї точки у кінце вий момент руху, він показує, де перебуватиме тіло через час руху t .

Тоді, щоб визначити зміну в по ложенні тіла за час руху, треба, як ви вже знаєте, знайти різницю між векторами r і r ₀ за правилом три кутника. Це буде вектор s , що з’єднує кінці цих векторів, він на прямлений до кінця вектора r :

r r ₀ r s .

Вектор s , проведений з початкового

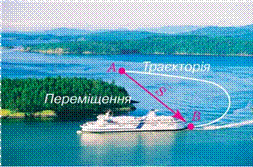Мал. 17 положення матеріальної точки до її кінцевого положення, називають пе/ реміщенням цієї точки за певний час.

Переміщення — дуже важлива фізична величина, що показує, на яку відстань і в якому напрямі змістилося тіло за даний час . Зна ючи, як переміщення змінюється з часом, можна розв’язати основну задачу для будьякого механічного руху. Як випливає з мал. 17, якщо відомі радіусвектор початкового положення тіла r ₀ і переміщення

^{Мал. 18} тіла s за час t , то радіусвектор r

кінцевого положення тіла можна визначити векторним додаванням цих векторів:

r r ₀ s .

Отриманий вираз називають рівнянням будьякого механічного руху у векторній формі, тут поточний радіусвектор і переміщення — функції часу: r r t ( ) і s s t ( ). Цей загальний векторний розв’язок основної задачі механіки дуже наочний, але їм не можна скористатися для безпосередньо го обчислення координат тіла у будьякий момент часу. Для цього його тре ба переписати у проекціях на осі координат , оскільки проекція вектора — це скаляр. Вираз у проекціях на координатну вісь буде мати такий самий вигляд, як і векторний вираз, але замість векторів треба записати відповідні проекції на осі координат. На мал. 17 маємо дві осі координат, тож наша векторна рівність розпадається на дві скалярні рівності (два рівняння руху) — для осей Ox і Oy :

x x 0 + s x ,

y y 0 + s y ,

Тут x ₀ , y ₀ , x , y , — проекції радіусвекторів r і r ₀ , які дорівнюють відповідним координатам їх кінців, s _x і s _y — проекції переміщення відповідно на осі Ox і Oy . Якщо початкові координати x ₀ , y ₀ перенести у ліву частину цих рівностей, то одержимо вирази для проекцій преміщення:

s x x x 0 x , s y y y 0 y .

Проекції переміщення s на осі коорди/ нат Ox і Oy дорівнюють змінам коорди/ нат тіла x і y .

Одержані скалярні вирази вже дають змогу, знаючи початкові координати точки і залежність проекцій переміщен ня від часу, обчислювати координати точки для будьякого моменту. Надалі якраз і будемо вивчати залежності про _{Мал. 19} екцій переміщення від часу для різних видів механічного руху, тобто знаходити рівняння руху для конкретних видів руху.

На мал. 18 показано криволінійну траєкто рію, яку тіло описало, руха ючись із точки А в точку В , і відповідне переміщення. Видно, що довжина (модуль) переміщення у загальному випадку менша за пройдений тілом шлях за певний інтервал часу. Тільки якщо, тіло рухається вздовж прямої і весь час в один бік, то пройдений ним шлях дорівнює модулю переміщення.

Під час руху шлях, пройдений тілом, з часом може тільки зростати, а переміщення, залежно від виду руху, з часом може зростати, зменшувати ся і, навіть, ставати нулем. Це буває, коли тіло, рухаючись, повертається у точку, з якої починало рух. Прикладом може бути рух тіла по колу (мал. 19). Як ми бачимо, під час руху тіла із точки А в точку В за годинни ковою стрілкою модуль його переміщення напочатку збільшується, поки не набуде максимального значення (діаметра кола), а потім зменшується і набуває значення нуля у точці початку руху.

1. Що таке траєкторія руху?

2. Чи залежить траєкторія руху тіла від системи відліку?

3. Що таке пройдений шлях?

4. Що називають радіусвектором точки?

5. Що називають переміщенням тіла?

6. Як за переміщенням визначити положення тіла під час руху?

7. Чим відрізняється переміщення від пройденого шляху?

8. Чому дорівнює переміщення годинникової стрілки за добу? за 2 год?

9. Коли пройдений шлях і переміщення будуть однаковими? Наведіть приклади.

10. Які переваги векторного опису механічного руху?

§ 6 РІВНОМІРНИЙ ПРЯМОЛІНІЙНИЙ РУХ. ШВИДКІСТЬ РУХУ ТІЛА

Найпрстішим є рівномірний рух тіла вздовж прямої в одному напрямі. З курсу фізики 8 класу ви знаєте, що прямолінійним рівномірним рухом на, зивають такий рух уздовж прямої, під час якого тіло за будь,які однакові інтервали часу проходить однакові шляхи . Дамо інше визначення такого руху і з’ясуємо певні відмінності.

Прямолінійним рівномірним рухом називають рух уздовж прямої, під час якого тіло за будь/які рівні інтервали часу здійснює однакові переміщення.

Обидва визначення прямолінійного рівномірного руху значною мірою еквівалентні щодо його ознак, але у другому визначенні фігурує векторна величина переміщення , на відміну від скалярного шляху , тобто у ньому враховано напрям руху тіла і тому нове визначення більш змістовне, оскільки дає змогу повніше і детальніше описати рух.

Дуже важливими у визначеннях прямолінійного рівномірного руху є те, що рівність шляхів, або переміщень розглядається за будь які рівні інтервали часу. Якби цієї умови не було, то можна було б підібрати для прикладу такі рухи, для яких ознака рівності шляхів виконувалася б для вибраних рівних інтервалів часу, а протягом цих окремих інтервалів умова рівності шляхівпереміщень не виконувалася б. У цьому разі рух безумов но не був би рівномірним, хоча ознака рівномірності формально і викону валася б. Умова визначення вимагає, щоб рівності переміщень виконува лись, наприклад, і для інтервалів 0,01 с, і для інтервалів 1 с, і для всіх довільних, що лежать поза межами цих значень.

Вимога рівності переміщень тіла за будьякі рівні інтервали часу є дуже жорсткою, тому на практиці рівномірні рухи бувають рідко. Проте на при кладі цього найпростішого виду руху можна дослідити більшість характе ристик механічного руху і використати їх для вивчення складніших рухів. Значною мірою прямолінійним і рівномірним рухом можна вважати рух металевої кульки у воді, дощових крапель, парашутиста під куполом парашута, транспортних засобів на окремих ділянках шляху.

Порівнюючи рух різних тіл, користуються такими характеристиками, як повільно , швидко , які є якісними і відносними. Щоб порівняти різні рухи кількісно, треба порівняти, наприклад, переміщення різних тіл за одиницю часу. Якщо за t одиниць часу здійснено переміщення s то


9-09-2015, 17:29