Федеральное агентство по образованию
Самарский Государственный Технический Университет
Нефтетехнологический факультет
Кафедра «Разработка и эксплуатация нефтяных и газовых месторождений»
КУРСОВАЯ РАБОТА
по дисциплине «Подземная гидромеханика углеводородов»
РАСЧЕТ ПОКАЗАТЕЛЕЙ РАЗРАБОТКИ ОДНОРОДНОГО ПЛАСТА
НА ОСНОВЕ МОДЕЛИ ДВУХФАЗНОЙ ФИЛЬТРАЦИИ
ДЛЯ ЖЕСТКОГО ВОДОНАПОРНОГО РЕЖИМА
(ПЛОСКОРАДИАЛЬНОЕ ДВИЖЕНИЕ)
Вариант № 70
Выполнил: студент , курс, группа
Проверил: преподаватель
Оценка: ________ «____»________ 200... г.
Самара 2006
Содержание
Задание……………………………………………………………………
1 Теоретическая часть.........................................................................
2 Расчетная часть……………………………….................................
Список использованных источников…………………………………...
Задание
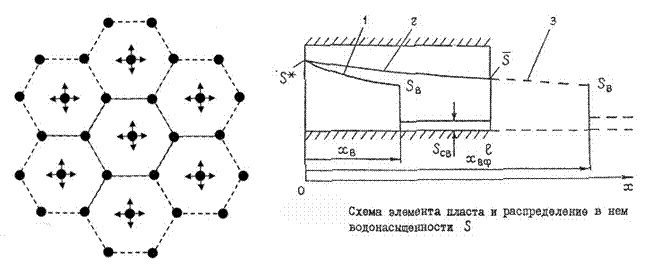
Нефтяное месторождение площадью F запланировано разрабатывать с использованием заводнения при однорядной схеме размещения скважин. Элемент однорядной схемы, содержащий одну нагнетательную скважину ("1/2 добывающей и 1/2 нагнетательной"), имеет ширину b и длину L.
Месторождение вводится в разработку за Т лет, причем за каждый год вводится в действие по N элементов. Разрабатываемый пласт месторождения имеет следующие параметры: общая нефтенасыщенная толщина h0 , абсолютная проницаемость К, пористость m, насыщенность связанной водой Scв , вязкость нефти в пластовых условиях µн , вязкость воды µв .
Пласт сравнительно однородный. Установлено, что вытеснение из него нефти водой происходит непоршневым способом. При этом относительные проницаемости для нефти Kн (S) и воды Kв (S), зависящие от водонасыщенности S, представлены в виде аналитических соотношений:
| ⎛ sx − s ⎞ Kн ( )s = ⎜ ⎝ sx − sсв⎠ |
при |
Sсв ≤ S ≤ Sx |
2
Kв ( )s = при Sсв ≤ S ≤ S1
 |
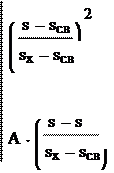
⎠ св ⎞ при S1 ≤ S ≤ Sx
При этом Scв и S* известны. Значение S1 определяется из условия равенства относительных проницаемостей для нефти и воды при S = S1 .
В пласт с линии нагнетания х = 0 закачивается вода с расходом q. Приемистость одной нагнетательной скважины составляет соответственно 2q. Коэффициент охвата пласта заводнением η2 . Добывающие скважины выбывают из эксплуатации при обводненности продукции, равной В.
Требуется:
1) определить изменение во времени добычи нефти, воды, обводненности продукции и текущей нефтеотдачи для элемента системы разработки и для месторождения в целом;
2) определить перепад давления в элементе системы разработки при хв = 0, хв = L/2 и хв = L;
если радиус нагнетательной скважины rнс = 0.1 м; а приведенный радиус добывающей скважины rс = 0.01 м;
площадь месторождения нефтенасыщенная толщина пласта коэффициент пористости абсолютная проницаемость насыщенность связанной водой предельная водонасыщенность динамическая вязкость нефти динамическая вязкость воды расход закачиваемой воды коэффициент охвата заводнением время ввода в разработку
число элементов площади, вводимых в эксплуатацию в течение полугода предельная обводненность
7 2 ;
F = 1.15 × 10 м h0 = 20 м; m = 0.21 ед; K = 0.27 мкм2 ; sсв = 0.15 ед; sх = 0.79 ед;
− 3
µн = 8 × 10 Пас;
− 3
µв = 1 × 10 Пас;
q = 200 м3 /сут; η2 = 0.79 ед;
T = 2.5 лет;
N = 20 ед;
B = 96.5 %;
Относительные проницаемости заданы в виде аналитических зависимостей.
2. Расчетная часть
Приступая к решению, определим прежде всего численное значение коэффициента А, входящего в приведенные зависимости Кн (S) и Кв (S). Для этого воспользуемся условием, что Кв (1) = 1. Имеем:
1 1
A === .86772 A = 0.868
⎛ 1 − sсв ⎞⎛ 1 − .15 ⎞
⎜ ⎝ sх − sсв⎠ ⎜ ⎝.79 − .15⎠
Примечание: Определение неизвестных, решение систем уравнений и прочие трудоемкие вычислительные задачи целесообразно решать, используя в качестве электронного калькулятора - ЭВМ. В данном случае используем математический пакет Mathcad и его оператор нахождения корней уравнений «Given и Find».
Теперь найдем S1 . Имеем:
Given
2 
⎛s1 − sсв⎞ ⎛s1 − sсв⎞
⎜ =
A ⋅ ⎜ ; => s1
= Find s( )1
; => s1
= 0.732
⎝ sх − sсв⎠ ⎝ sх − sсв⎠
Строим зависимость относительных фазовых проницаемостей от водонасыщенности, задаваясь значениями S в пределах от Scв до 1. При этом пользуются следующими уточненными выражениями относительных фазовых проницаемостей: s = sсв ,sсв + 0.01 ..sх
2
⎛ sх
− s ⎞ Kн
( )s = ⎜
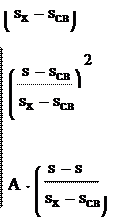
Kв
( )s =if sсв
≤ s ≤ s1
⎠
св ⎞ if s1 ≤ s ≤ sх Относительные проницаемости
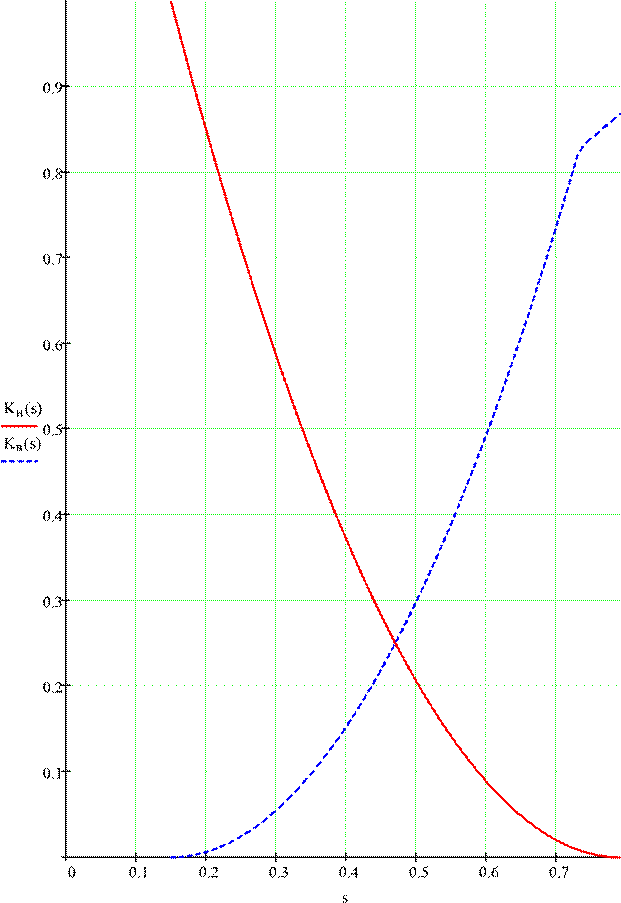
Рисунок 7
Таким образом, при sсв ≤ s ≤ s1 где s1 = 0.732 функция Бэкли-Леверетта
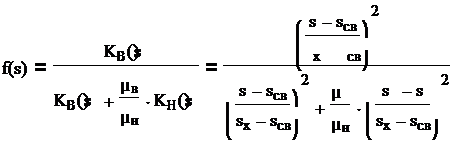s − s
⎛ в ⎛ х ⎞
или f(s) 
µ
2 в 2
(s − sсв
) + 
⋅ (sх
− s)
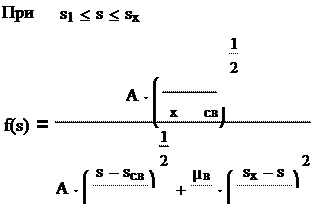µн
s − sсв
⎞ s − s
⎝ sх − sсв⎠ µн ⎝ sх − sсв⎠
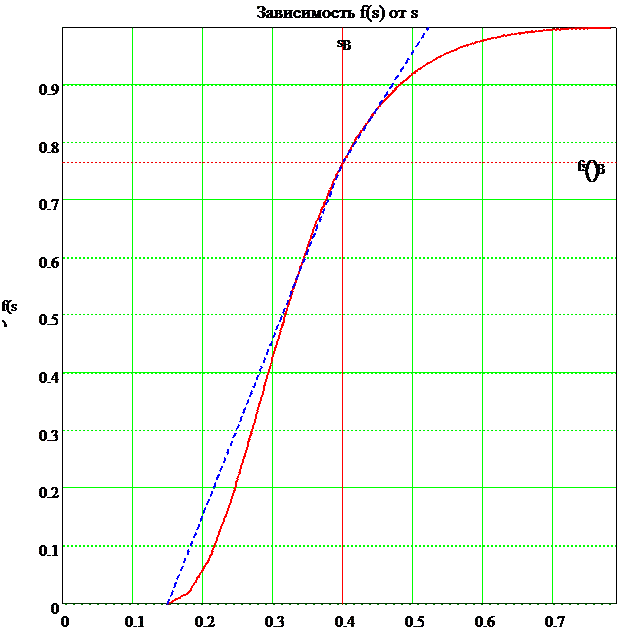
При построении кривой применим ЭВМ. Зададим условия и пределы построений:
s = sсв ,sсв + 0.03 ..sх
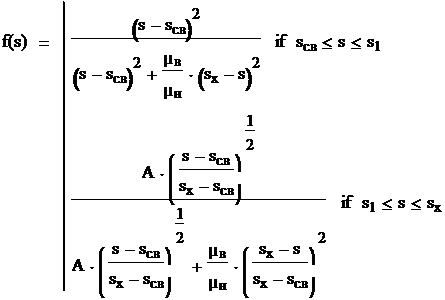
Касательную построим вручную, что упрощает расчет, но проигрываем в точности.
sB = 0.4 f s ( )B = 0.767
s(x)
Рисунок 8
Из кривых (рисунок 8) ОФП видно, что (S*) = 1 .
| 0 |
0.15 |
| 0.019 |
0.18 |
| 0.079 |
0.21 |
| 0.176 |
0.24 |
| 0.299 |
0.27 |
| 0.428 |
0.3 |
| 0.551 |
0.33 |
| 0.656 |
0.36 |
| 0.742 |
0.39 |
| 0.81 |
0.42 |
| 0.862 |
0.45 |
| 0.901 |
0.48 |
| 0.93 |
0.51 |
| 0.951 |
0.54 |
| 0.967 |
0.57 |
| 0.978 |
0.6 |
| 0.986 |
0.63 |
| 0.992 |
0.66 |
| 0.996 |
0.69 |
| 0.998 |
0.72 |
| 0.999 |
0.75 |
| 1 |
0.78 |
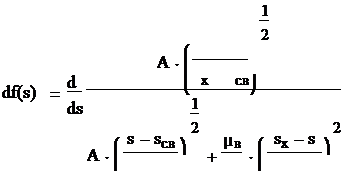f(s) = s = Теперь необходимо построить кривую f '(s). Функцию f '(s) получим путем обычного дифференцирования функции f(s).
Таким образом, при sсв ≤ s ≤ s1
(s − sсв)2
df(s) =
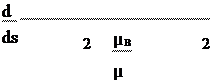(s − sсв
) + ⋅ (sх
− s)
При s1 ≤ s ≤ sх н
s − sсв ⎞ s − s
⎝ sх − sсв⎠ µн ⎝ sх − sсв⎠
Делаем проверку удовлетворяется ли условие на входе в пласт, то есть при х = 0, где s = sх .
Примечание: Здесь мы можем опустить процесс отыскания производной, но при этом получаем все необходимые данные по последоваельности расчета.
(s − sсв)2
При s = sсв df(s) =df(s) = 0
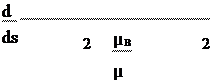(s − sсв
) + ⋅ (sх
− s)
н
s = sсв ,sсв + 0.01 ..sх
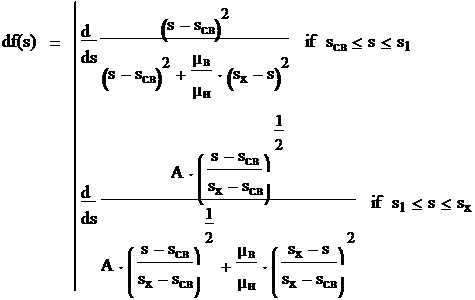
При s. = sB df(s) = 2.348
|
Теперь легко определить время безводной разработки элемента пласта.
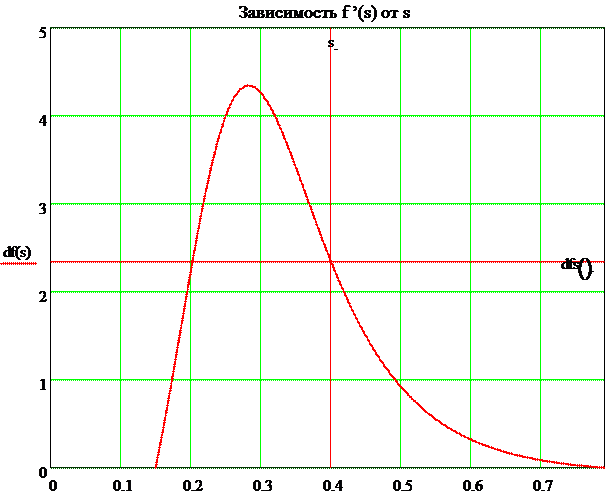
s
Рисунок 9
Здесь h0 ⋅ η2 - охваченная заводненном толщина пласта.
h = h0 ⋅ η2 = 20. ⋅ .79 = 15.80 м;
Площадь кругового элемента Fэ определяют, зная общую площадь месторождения, а также сроки и темпы его ввода в эксплуатацию. Для заданных условий:
F 11500000.
Fэ
= = = 115000.00 м2
; 2 ⋅ N ⋅ T 2 20.⋅ ⋅ 2.5
Радиус кругового элемента, эквивалентного семиточечному элементу площади;
rk
= 
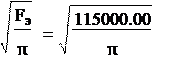= 191.326 м;
2 2
rk ⋅ h ⋅ m ⋅ π 191.326 ⋅ 15.80 ⋅ .21 ⋅ π
Имеем: txсут
суток;
txсут 812.575
tx
= = = 2.2262 года;
365 365
| Накопленное количество добытой нефти за период безводной разработки |
|
| пласта: Qнх = q t⋅ xсут = 200. 812.575⋅ = 162515.000 м3 ; Безводная нефтеогдача: |
|
| η2 .79 η0 = = = .39585 |
η0 = 0.396 |
df(sB) ⋅ (1 − sсв
) 2.3479 ⋅ (1 − .15)
| 0 |
0.15 |
| 1.303 |
0.18 |
| 2.672 |
0.21 |
| 3.757 |
0.24 |
| 4.297 |
0.27 |
| 4.265 |
0.3 |
| 3.825 |
0.33 |
| 3.198 |
0.36 |
| 2.551 |
0.39 |
| 1.973 |
0.42 |
| 1.496 |
0.45 |
| 1.12 |
0.48 |
| 0.83 |
0.51 |
| 0.61 |
0.54 |
| 0.444 |
0.57 |
| 0.319 |
0.6 |
| 0.225 |
0.63 |
| 0.154 |
0.66 |
| 0.101 |
0.69 |
| 0.06 |
0.72 |
| 0.03 |
0.75 |
| 7.117·10-3 |
0.78 |
df(s) = s = Чтобы определить текущую обводненность продукции v и текущую нефтеотдачу η в водный период разработки, используем формулу, которая применительно к рассматриваемому случав принимает следующий вид:
df s( )a tx txсут ⋅ sB
=
или df s( )a
= 
df s( )B t t
Задавая различные значения t, определяем f '(S), а затем по графику (рисунок 10) - искомое значение Sа .
txсут ⋅ dfs B
t = 0.5 0.5, + 0.5 ..15 dfsa
( )t = 
t 365⋅
txсут ⋅ df(sB) 812.575 ⋅ 2.3479
dfsa
( )tx
= = = 2.3479
tx ⋅ 365 2.2262 365⋅
Покажем на графике значение Sа при tx и в функции времени.
Обычная методика
Строим при помощи ЭВМ вспомогательные вертикальные линии - пересечение производной функции fSa(t) (как функция от Sa) с искомыми точками Sa, по которым и находим точное значение Sa. Далее на рисунке показана производная функции f(S) и вертикальные линии проецируя точку на ось ординат - определяем соответствующее значение производной функции f(Sa).
|
Т.е. по горизонтальной оси для производных функций fSa(t) и f(S) имеет место разная размерность, соответственно - t и S. Поэтому искомые значения Sa определяются графически (визуально).
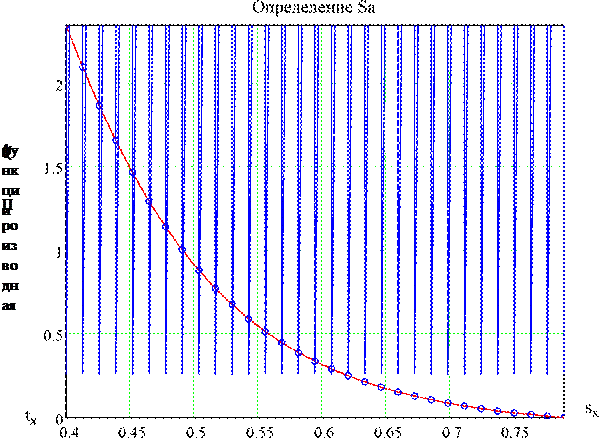
Водонасыщенность, время
Рисунок 10
Автоматизированная методика
Предыдущая методика отличается неточностью и неоправданными трудозатратами. При помощи программы Mathcad производим сплайновую аппроксимацию (линейный сплайн) для функции f(S) + S и строим тождественную предыдущему рисунку кривую f(S). Но точки на рисунке 10 произвольны и не соответствуют принятой кратности периодов разработки скважин - 0,5 лет.
Поэтому необходимо аппроксимировать также функции f(Sа) + S и определить значения Sа для моментов, кратным 0,5 лет. Рисунок 11 строить нет необходимости, т.к. он является лишь проверкой соответствия стандартному расчету и скорректирован для моментов, кратных 0,5 лет.
Значения Sа определяются подстановкой в аппроксимированную функцию f(Sа) + S значений f(Sа) для моментов времени t кратных 0,5 лет.
Определение Sa
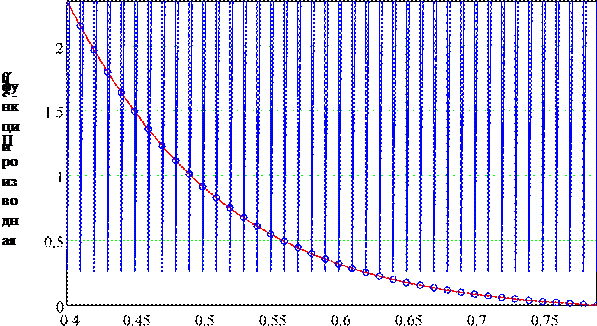
Водонасыщенность, время
| Результаты определения Sa |
Рисунок 11 |
||
| S1 = 0.4 |
dSa1 = 2.348 |
S2 = 0.434 |
dSa2 = 1.742 |
| S3 = 0.45 |
dSa3 = 1.493 |
S4 = 0.464 |
dSa4 = 1.307 |
| S5 = 0.476 |
dSa5 = 1.162 |
S6 = 0.487 |
dSa6 = 1.045 |
| S7 = 0.497 |
dSa7 = 0.95 |
S8 = 0.505 |
dSa8 = 0.871 |
| S9 = 0.513 |
dSa9 = 0.804 |
S10 = 0.52 |
dSa10 = 0.747 |
| S11 = 0.527 |
dSa11 = 0.697 |
S12 = 0.533 |
dSa12 = 0.653 |
| S13 = 0.539 |
dSa13 = 0.615 |
S14 = 0.545 |
dSa14 = 0.581 |
| S15 = 0.55 |
dSa15 = 0.55 |
S16 = 0.555 |
dSa16 = 0.523 |
| S17 = 0.559 |
dSa17 = 0.498 |
S18 = 0.564 |
dSa18 = 0.475 |
| S19 = 0.568 |
dSa19 = 0.455 |
S20 = 0.572 |
dSa20 = 0.436 |
| S21 = 0.576 |
dSa21 = 0.418 |
S22 = 0.579 |
dSa22 = 0.402 |
| S23 = 0.583 |
dSa23 = 0.387 |
S24 = 0.586 |
dSa24 = 0.373 |
| S25 = 0.589 |
dSa25 = 0.36 |
S26 = 0.592 |
dSa26 = 0.348 |
| S27 = 0.595 |
dSa27 = 0.337 |
S28 = 0.598 |
dSa28 = 0.327 |
| S29 = 0.601 |
dSa29 = 0.317 |
S30
=
Разделы сайта | |