ВІДПОВІДІ НА ЗАВДАННЯ ТЕСТУ З МАТЕМАТИКИ (ІІ СЕСІЯ)

(Затверджені експертною комісією Українського центру оцінювання якості освіти

27 червня 2008 року)

Частина 1

Завдання 1-25 мають по п'ять варіантів відповіді, серед яких лише ОДИН ПРАВИЛЬНИЙ.

1. Укажіть, яку з указаних цифр потрібно підставити замість * в число 2345* , щоб воно ділилося на 3 без остачі.

Відповідь : 4.

Бевз Г.П. Математика: 6 кл. : Підручник для загальноосвіт. навч. закл. /Г.П.Бевз, В.Г.Бевз. ─ К.: Генеза, 2006 ─ С. 15.

2. Визначте кількість усіх дробів із знаменником 24, які більші за , але менші за 1.

Відповідь : 3.

Мерзляк А.Г., Полонський В.Б., Якір М.С. Математика: Підручник для 6 класу. ─ Х.: Гімназія, 2006 ─ С. 51.

3. У кабінеті математики 50% всіх книг – підручники з алгебри, 25% решти книг – підручники з геометрії, а інші книги – посібники з підготовки до ЗНО. Укажіть, на якій із діаграм правильно показано розподіл книг.

Відповідь :

Янченко Галина, Кравчук Василь. Математика: Підручник для 6 класу. ─ Тернопіль: Підручники і посібники, 2006 ─ С.149

x +3

4. Розв’яжіть нерівність <0. x −1

Відповідь : (– 3;1).

Бевз Г.П. Алгебра: Підручник для 9 кл.загальноосвіт. навч. закладів. ─ К.: Освіта, 2006 ─ С. 21.

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підруч. для 11 кл.

загально освіт. навч. закладів. – К.: Зодіак – ЕКО, 2003. − С. 362.

2 mv

5. Якщо R = , де v > 0, m ≠ 0, T ≠ 0, то v =

2T

2RT

Відповідь : . m

Бевз Г.П. Алгебра: Підруч. для 8 кл. загальноосвіт. навч. закл. ─ К.: Освіта, 2004 ─ С. 55.

6. Серед учнів одного класу проведено опитування щодо кількості книг, прочитаних ними під час літніх канікул. Результати цього опитування подано в таблиці.

(Х − кількість книг, прочитаних учнем за канікули, М − кількість учнів, які прочитали таку кількість книг). На якому з указаних полігонів правильно проілюстровано заданий розподіл частот?

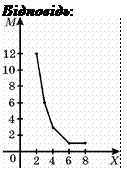
Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 11 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2005. – С. 329.

Бевз Г.П. Алгебра: Підручник для 9 кл. загальноосвітніх навчальних закладів. –К.: Освіта, 2006. − С. 92.

7. Порівняйте задані числа 4; 2 5 ; 17 .

Відповідь : 4 < 17 < 2 5 .

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2004 – С.262.

⎛ π π⎞²

8. Обчисліть_⎜ sin − cos _⎟ .

⎝ 12 12 ⎠

Відповідь : .

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. − С. 96.x

9. Укажіть найменший додатний період функції y = 3cos .

2 Відповідь : 4π.

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. − С. 48.

10. Графік функції f (x ) проходить через точку, зображену на рисунку. Укажіть функцію f (x ).

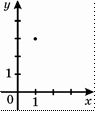
Відповідь : f x ( ) = 3^x .

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2004. − С.18.

11. Обчисліть lg(5a ) + lg(2b ), якщо lg(ab ) = 5.

Відповідь : 6.

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. − С.224.

12. Розв’яжіть рівняння sin x +cosx = 0.

Відповідь : Z .

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2004. − С.173.

13. Укажіть, скільки можна скласти різних двоцифрових чисел із цифр 1; 2; 3; 4; 5; 6; 7; 8; 9, не повторюючи цифри в числі. Відповідь : 72.

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2004. − С.236.

14. Розв’яжіть нерівність log_0,7 x > log_0,7 8.

Відповідь : (0; 8).

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. − 234 с.

15. Розв’яжіть рівняння x ² +2x =1.

Відповідь : −1; − −1 2 ; − +1 2 .

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 11 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2006. − С.5.

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2004. − С.242.

16. Розв’яжіть рівняння 5^x = .

Відповідь : .

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2004. − С.339.

17. Укажіть область ЗНАЧЕНЬ функції y = 5−2sin x .

Відповідь : [3; 7].

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. − §1.

18. На рисунку зображено графіки функцій y = f (x ) та y = g (x ), задані на проміжку [–5; 5]. Укажіть усі значення x , для яких виконується нерівність f (x ) ≤ g (x ).

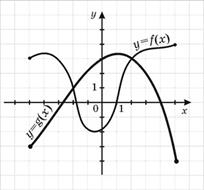
Відповідь : [–2; 2].

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2004. − С.101.

x

19. На рисунку зображено графіки функцій y = x та y = . Укажіть формулу для

2

обчислення площі заштрихованої фігури.

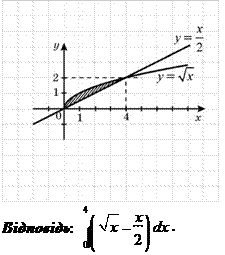
Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 11 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2006. − С. 143.

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 11 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2005. – С. 209.

x −5

20. Знайдіть значення виразу , якщо х = 4,5.

25 10− x +x ²

Відповідь : – 1.

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. −С.139.

21. Тіло рухається прямолінійно за законом s (t ) = t ² (t + 2 ) (час t вимірюється в секундах, шлях s – у метрах). Визначте його швидкість (у м / с ) через 2 секунди після початку руху.

Відповідь : 20.

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 11 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2005. – С. 31.

22. У трикутнику ABC ∠A = 42°, ∠B = 64°. Із вершин кутів A і C проведені бісектриси трикутника, які перетинаються в точці O . Визначте величину кута AOC .

Відповідь : 122°.

Погорєлов О.В. Геометрія: Планіметрія: Підруч. для 7-9 кл. загальноосвіт. навч. закл.-К.: Школяр, 2004. – С.53.

23. Сторони трикутника, одна з яких вдвічі більша за другу , утворюють кут 120°, а довжина третьої сторони дорівнює 3 7 . Знайдіть найменшу сторону трикутника.

Відповідь : 3.

Бевз Г.П. та інші. Геометрія: Підручник для 7 − 9 кл. загальноосвітніх навчальних закладів. – К.: Вежа, 2004. − С.194-195.

24. На рисунку зображено розгортку поверхні тіла, складену з шести попарно рівних прямокутників, розміри яких указано. Обчисліть об’єм цього тіла.

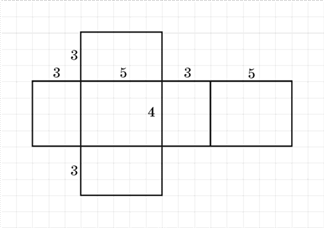
Відповідь : 60 см ³ .

Погорєлов О.В. Геометрія: Стереометрія: Підруч. для 10 - 11 кл. серед. школ.-К.: Освіта, 1994. – С.100.

25. З дерев’яної циліндричної заготовки, осьовим перерізом якої є квадрат, виточили більярдну кулю найбільшого об’єму (див рисунок). Визначте відношення об’єму кулі до об’єму всієї заготовки.

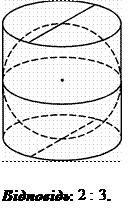
Погорєлов О.В. Геометрія: Стереометрія: Підруч. для 10 - 11 кл. серед. школ.-К.: Освіта,1994.

Частина 2

Розв’яжіть завдання 26-33. Запишіть відповідь у зошит і бланк А.

⎛ 4⎞ ⎝ 5⎠

26. Обчисліть 8ctg arcsin⎜ _⎟ .

Відповідь: 6.

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2007. − С.148.

27. Обчисліть суму перших десяти членів арифметичної прогресії, у якої a ₁ = 2, a ₂ = 5.

Відповідь: 155.

Бевз Г.П. Алгебра: Підручник для 9 кл. загально освіт. навчал. закл. К.: Освіта, 2006. – С.74.

28. Розв’яжіть рівняння x − −2 2x ² − − =9 2x 0. Якщо рівняння має кілька коренів, то у відповідь запишіть їх суму.

Відповідь: 6.

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 10 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2002. −С.158.

29. До водно-сольового розчину з концентрацією солі 0,25 долили 100 г води й одержали розчин з концентрацією солі 0,2. Знайдіть початкову масу розчину в грамах .

Відповідь : 400.

Бевз Г.П. Алгебра: Підручник для 9 кл. загально освіт. навчал. закл. К.: Освіта, 2006. – С.9498.

30. В сумці лежать яблука, серед яких 8 – червоні, решта – жовті. Знайдіть кількість жовтих яблук, якщо імовірність витягти навмання червоне яблуко дорівнює 0,4.

Відповідь : 12.

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 11 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2006. − С.230.

⎧x ² + =y ² 4,

31. Знайдіть усі значення параметра a , при яких система рівнянь ⎨ ₂ має єдиний

_⎩ y x = +a розв’язок (якщо таких значень кілька, то до відповіді запишіть їх суму ).

Відповідь : 2.

Бевз Г.П. Алгебра: Підручник для 9 кл. загально освіт. навчал. закл. К.: Освіта, 2006. – С.49.

r r r r

32. Визначте кут між векторами a b − і c у градусах, якщо відомо, що a (3; 5; − 4) , r r b ( 2− ; 5; − 4) і c (0; 0; 2).

Відповідь: 90.

Погорєлов О.В. Геометрія: Стереометрія: Підруч. для 10 - 11 кл. серед. школ.-К.: Освіта,2004.

33. Висота конуса дорівнює 4 см, радіус основи – 3 см. Знайдіть відношення площі основи конуса до площі його бічної поверхні. Відповідь запишіть десятковим дробом .

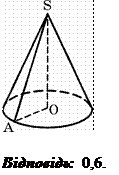
Погорєлов О.В. Геометрія: Стереометрія: Підруч. для 10 - 11 кл. серед. школ.-К.: Освіта, 2004, с.117.

Частина 3

34. В основі піраміди лежить прямокутний трикутник з катетом a і прилеглим до нього кутом β. Бічні грані піраміди, які містять катети цього трикутника, перпендикулярні до площини основи, а третя бічна грань нахилена до основи під кутом ϕ. Знайдіть висоту піраміди.

Відповідь: a sinβ tgϕ .

Погорєлов О.В. Геометрія: Стереометрія: Підруч. для 10 - 11 кл. серед школ.-К.: Освіта, 2004, с.12, 50.

10x −x ² x −4

35. Розв’яжіть нерівність 5> 0,2 .

Відповідь: x ∈ (1; 10].

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 10 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2007. − С. 232, 308, 351.

36. Задано функцію f (x ) = 4 x ⁶ −6 x ⁴ + 3.

1. Знайдіть проміжки зростання та спадання функції, точки екстремуму функції, а також значення функції в цих точках.

2. Побудуйте ескіз графіка функції.

3. Знайдіть усі значення параметра а , при яких рівняння f (x ) = а має точно два різних корені.

Відповідь:

1. Функція f (x ) зростає на кожному з проміжків (−1; 0) та (1; + ∞) і спадає на кожному з проміжків (−∞; −1) та (0; 1).

(Враховуючи неперервність функції f (x ) до проміжків зростання і спадання функції можна включити також точки −1; 0; 1).

3. Рівняння f (x ) = а має точно два різних корені при а ∈ ( 3; + ∞) та при а = 1.

Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підручник для 11 класу загальноосвітніх навчальних закладів. – К.: Зодіак – ЕКО, 2006. − С.112.

Нелін Є.П. Алгебра і початки аналізу: Дворівневий підручник для 11 класу загальноосвітніх навчальних закладів.−Х.: Світ дитинства, 2007. − С. 90.