,

Схема астрономо-геодезической сети представляет собой полигон с привязкой к исходному пункту (рисунок 5). Среднее расстояние между пунктами - 4км. В качестве измерений выступают разности высот квазигеоида, вычисляемые по составляющим уклонений отвесных линий.
Формула для вычисления разности высот квазигеоида имеет вид:
![]() (4)
(4)
где D 12 – расстояние между пунктами 1 и 2;
ξ , η – составляющие уклонения отвеса;
A 12 - геодезический азимут направления с пункта 1 на пункт 2.
Уравнивание астрономо-геодезической сети выполнено коррелатным способом.
Для астропункта 20А аномалия высоты принята равной нулю. Пользуясь уравненными значениями аномалий высот zi , построим плоскость, наилучшим образом приближенную к астропунктам на поверхности квазигеоида.
Отклонения от неё nz i будут характеризовать степень неоднородности гравитационного поля.
Именно они могут оказывать влияние на результаты физических экспериментов. В таблице 3 приведены значения отклонений nz i . Величины отклонений nz i от вероятнейшей плоскости не превышают ср. кв. погрешности их определения (~1,1мм).
Использование астрономических наблюдений позволило выявить характер гравитационного поля в пределах объекта строительства: наклон проектной плоскости орбиты ускорителя, вызываемый постоянной составляющей аномалий высот на 5-ти астропунктах, уверенно прослеживается в направлении с северо-востока на юго-запад. По отношению к заданному наклону проектной плоскости (0,67мрад) эта величина невелика (0,01мрад) и может не учитываться.
Таблица 3
Результат вычисления положения вероятнейшей плоскости по значениям аномалий высот астропунктов наземной сети УНК
| астропункт |
Уравненные аномалии высот |
Составляющие аномалий высот |
|
| образуют вероятнейшую плоскость |
отклонения от вероятнейшей плоскости |
||
| zi , мм |
zi ¢,мм |
nz I , мм |
|
| 20A 511A 14A 10A 7A |
0,00 24,19 61,43 85,08 25,58 |
-0,19 +25,15 +60,25 +85,68 +25,37 |
+0,19 -0,96 +1,18 -0,60 +0,20 |
В пятой главе «Разработка методики анализа результатов наблюдений за деформациями плановой наземной геодезической основы» рассматриваются теоретические основы оценивания внутренних деформаций плановых сетей на основе принципа конформного преобразования. В связи с тем, что для кольцевых ускорителей важно знать величины деформаций по радиусу и азимуту, алгоритм доработан с целью применения его в системе полярных координат.
Накопление случайных и систематических погрешностей в протяженных геодезических сетях приводит к тому, что значения полной деформации, определенные как разность координат одноимённых пунктов из 2-х циклов измерений, не всегда соответствуют фактическим смещениям. В результате уравнивания наземной сети УНК координаты наиболее удалённых от исходного пунктов определяются с погрешностями, достигающими 50мм. Поэтому при обработке деформационных измерений было принято решение использовать метод разделения полной деформации δх j и δу j на две составляющие – внутреннюю δх j + δ у j + и внешнюю δxj ( β ) δyj ( β ):
![]()
![]() (5)
(5)
![]()
Внутренняя деформация характеризует взаимное смещение плановых пунктов. Внешняя деформация пунктов сети определяется набором параметров, связанных с её разворотом относительно исходной точки, изменением линейного масштаба, параллельным сдвигом по осям координат. Нормальная работа кольцевого ускорителя не зависит от внешней деформации, но чувствительна к взаимному смещению пунктов. Автором предлагается следующая последовательность оценивания внешних и внутренних деформаций.
1. Уравниваются начальный и текущий циклы измерений с одной твёрдой точкой и исходным дирекционным углом (нуль-свободная сеть).
2. Вычисляется полная деформация сети:![]()
δ xj = xj – xj 0
δyj = yj – yj 0 . (6)
3. Осуществляется переход от нуль-свободной сети к свободной: координаты j –ой точки вычисляются от центра тяжести:
![]() xj
=
x
0
+
Lj
cosα
xj
=
x
0
+
Lj
cosα
yj = y 0 + Lj sinα , (7)
где x 0 =[ xj ]/ N , y 0 =[ yj ]/ N .
4. Полный дифференциал от выражения (7) даёт формулу определения внешней составляющей деформации (8) c учётом того, что δ m = δ L / L . Её компоненты интерпретируются как дифференциалы изменения координат в определенной системе, обусловленные конформным преобразованием, сохраняющим геометрию сети:
![]()
![]()
![]() , (8)
, (8)
где ![]() ,
, ![]()
δх0 , δу0 - параметры конформного преобразования, приводящие к
сдвигу сети относительно центра тяжести по осям координат х и у ;
δ m – параметр изменения масштаба;
δα – параметр связанный с разворотом системы координат.
5. Вычисляется величина внутренней деформации как разность между полной деформацией и её внешней составляющей:
![]()
![]()
![]() . (9)
. (9)
Параметры конформного преобразования определяются по способу наименьших квадратов под условием ![]() .
.
6. Ср.кв. погрешность внутренней деформации вычисляется по известной формуле: ![]() (10),
(10),
в которой матрица весовых коэффициентов для декартовой системы координат: ![]() (11)
(11)
В формуле (11) матрица ![]() (12)
(12)
где I – единичная матрица размера 2N(2N – количество пунктов в сети);
е – матрица, составленная из частных производных равенств (7):
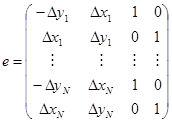 . (13)
. (13)
7. Внутренняя деформация в декартовой и полярной системах координат представляется в матричном виде:
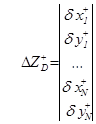 ;
; 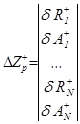 . (14)
. (14)
8. Переходим от декартовой системы координат к полярной следующим образом: Δ Zp + = B 2 N ×2 N ΔZD + , (15)
где В – матрица, составленная из коэффициентов равенств, выражающих смещение координат по радиальному и азимутальному направлениям:
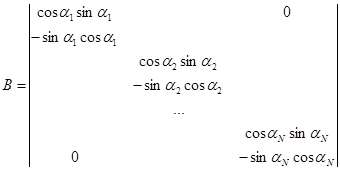 . (16)
. (16)
9.Получаем матрицу весовых коэффициентов для полярной системы координат, пользуясь аналогичной матрицей для декартовой системы из уравнивания текущего цикла нуль-свободной сети:
![]() (17)
(17)
10. Вычисляется ср. кв. погрешность определения внутренней деформации по приведённой ниже формуле (в общем виде) при использовании погрешности единицы веса для текущего цикла измерений:
![]() . (18)
. (18)
Алгоритм был использован при составлении вычислительной программы для компьютерной обработки деформационных измерений на УНК.
Достоверность определения внутренней деформации по приведённой методике подтверждалась проведённым сравнительным анализом результатов её вычисления с результатами, полученными по способу гармонического анализа и при уравнивании сети как свободной по методу наименьших квадратов. По известным формулам были получены величины внутренней деформации в полярной системе координат и их ср.кв. погрешности для модели полигонометрической сети в виде правильного 6-угольника, совпадающие при вычислении разными методами.
В шестой главе «Практическая реализация методических положений по развитию геодезического обоснования для обеспечения строительства и монтажа технологического оборудования УНК» обобщены результаты практической реализации разработок автора.
При создании наземной локальной астрономо-геодезической сети СКП измерения сторон была задана величиной ±5мм, углов – 1,2″, астрономические измерения на 6-ти пунктах Лапласа проводились по 1-ому классу точности. Обработка геодезических измерений включала редукционные вычисления с учётом выбранного осевого меридиана плоскости проекции Гаусса и приведением к принятой поверхности относимости. Анализ уравнивания нескольких циклов измерений показал, что наиболее слабым в точностном отношении пунктом оказался пункт 0012. СКП определения его координат: mx = 15,0мм, my = 22,0мм не превысили заданной техническим заданием предельной величины 25мм. Выбранная схема, метод создания наземной сети и качественные измерения позволили создать наземную геодезическую основу, соответствующую проектным требованиям.
Разработанная технология геодезических работ по развитию наземного и подземного обоснования при сооружении тоннеля обеспечила одну из главных задач – сбойку встречных подземных выработок в соответствии с заданными в техническом задании допусками. По результатам 6-ти сбоек максимальная величина несбойки встречных осей тоннелей в плане составила 21мм при допуске 25мм, а по высоте – 13мм при допуске 15мм.
В результате математической обработки геодезических измерений и последовательного уравнивания маркшейдерской и монтажной сети с СКП исходных данных были получены результаты, приведённые в таблице 4. Т а б л и ц а 4
Точность определения координат исходных пунктов маркшейдерской сети после уравнивания повысилась в 1,4 раза, после уравнивания монтажной сети – в 1,2 раза. При погрешности передачи координат на исходные квадруполи 0,5 ÷ 1,0мм, СКП определения их положения относительно пунктов наземной сети не превысят заданной техническим заданием величины 5,0мм.
Результаты оценки точности исходных пунктов на отдельных этапах создания подземного геодезического обоснования
| Средняя квадратическая погрешность (СКП) |
Минимальное значение |
Максимальное значение |
Среднее значение |
|||
| mх ,мм |
mу ,мм |
mх ,мм |
mу ,мм |
mх ,мм |
mу ,мм |
|
| СКП приствольного пункта на поверхности относительно пункта тоннельной сети |
3,9 |
4,1 |
||||
| СКП исходных пунктов маркшейдерской сети относительно пунктов наземной сети (из 19-ти передач) |
4,0 |
2,8 |
9,9 |
10,3 |
6,1 |
6,1 |
| СКП исходных пунктов маркшейдерской сети после уравнивания с ошиб. исход. данных |
3,6 |
2,7 |
6,0 |
6,7 |
4,5 |
4,4 |
| СКП исходных пунктов монтажной сети после уравнивания с ошибками исходных данных (12 пунктов) |
1,6 |
2,6 |
4,8 |
5,3 |
3,6 |
3,7 |
Предложенная методика вычисления деформаций применялась при обработке восьми циклов плановых измерений наземной сети. Предварительно оценивалась точность полевых измерений. Усреднённые значения погрешностей определения углов и сторон mβ = 1,18″, mS = 4,8мм не превысили проектных значений. В результате уравнивания по специальной программе вычислялись величины деформаций в декартовой и полярной системах координат. На рисунке 6 приведены графики внутренней деформации пунктов по радиусу R и азимуту А в восьмом цикле измерений относительно первого.
Величины внутренних деформаций пунктов в радиальном направлении по результатам четырёхлетних наблюдений не превысили 13мм для кольцевой сети диаметра 6км. Точность определения внутренней деформации составила в среднем mδR = 9,8мм.

Основные результаты исследований состоят в следующем:
1. Анализ результатов математического моделирования вариантов построения наземной геодезической основы (триангуляции, трилатерации, линейно-угловой сети, полигонометрии и специальной полигонометрии с измеренными астрономическими азимутами) показал, что выбор полигонометрической сети с измеренными астрономическими азимутами является наиболее оптимальным и с точки зрения обеспечения проектной точности, и по экономико-организационным показателям.
2. В результате решения редукционных задач автором предложено при вычислениях использовать осевой меридиан, максимально приближенный к центру кольцевого ускорителя. Расчёты показали, что при этом условии поправки в линейные и угловые измерения за переход на плоскость в проекции Гаусса-Крюгера не вводятся на всех этапах создания наземного и подземного обоснования. Необходимо вводить редукционные поправки в измеренные линии наземной полигонометрии (при длинах более 400м) при переходе к поверхности относимости со средней отметкой оси тоннеля 118м.
3. Теоретическое исследование, связанное с учётом влияния на результаты высотных измерений кривизны поверхности относимости при строительстве тоннеля и монтаже технологического оборудования, доказало достаточность использования в качестве этой поверхности в первом случае – сферы, во втором случае – эллипсоида. Автором рекомендуется вычисления производить относительно поверхности эллипсоида и вводить поправки за кривизну поверхности относимости при расчёте проектных высот орбиты ускорителя.
4. Разработанный метод оценки степени влияния неоднородности гравитационного поля на результаты высотных измерений по данным астрономо-геодезического нивелирования позволил выявить дополнительный наклон проектной плоскости кольцевого ускорителя (0,014мрад). Составляющая аномалии высоты, характеризующая однородность гравитационного поля zi ¢, не учитывается, т.к. не деформирует плоскость орбиты ускорителя. Переменная составляющая nz i , характеризующая неоднородность гравитационного поля в пунктах Лапласа, имеет максимальную величину 1,18мм, соответствующую пределу точности измерений.
5. Разработан и применён алгоритм определения внутренней деформации плановых геодезических сетей на основе принципа конформного преобразования в полярной системе координат.
6. Выполненные исследования по оценке точности внедрённой технологии на всех этапах создания геодезического обоснования УНК позволили получить точностные данные для метрологической аттестации методик геодезических измерений в рабочих условиях строительства и монтажа УНК.
Публикации по теме диссертации
1. В.А.Горелов, Г.В.Глухов, Е.Д.Лавриненко. Создание планового геодезического обоснования при строительстве УНК. Известия вузов.Геодезия и аэрофотосъёмка - 2002.№3 - с.3-14.
2. В.А.Горелов, Г.В.Глухов, Е.Д.Лавриненко. Принцип преемственности и его роль при построении геодезических сетей на поверхности и в тоннеле УНК. Известия вузов. Геодезия и аэрофотосъёмка - 2002.№3 - с.15-21.
3. В.А.Горелов, Е.Д.Лавриненко, В.П.Савушкина. Влияние кривизны поверхности относимости при строительстве тоннеля и монтаже оборудования УНК по высоте. Современные методы проектирования, технической эксплуатации и реконструирования зданий и сооружений: Сборник трудов МГСУ - М, 2005 - с.145-147.
4. В.А.Горелов, Е.Д.Лавриненко. Методика обработки плановых деформаций наземной геодезической основы ускорительно-накопительного комплекса (УНК). Геодезия. Международная научно-техническая конференция, посвященная 225-летию МИИГАиК: Сборник докладов – М, 2004 -с.242-250.
5. Е.Д.Лавриненко, В.А.Горелов, Л.Г.Шкулепова. Учёт влияния гравитационного поля по данным астрономо-геодезического нивелирования при монтаже технологического оборудования ускорительно-накопительного комплекса (УНК). Современные технологии геодезического обеспечения строительства, монтажа и геотехнического мониторинга зданий и сооружений: Юбилейный сборник трудов МГСУ- М, 2006 - с.133-139.
29-04-2015, 00:33
