Высшая геодезия
Отчет по курсовой работе на тему:
«Обоснование точности измерений и допусков при развитии геодезических сетей специального назначения »
Вариант № 22
Задание № 51
Преподаватель Студент 152 гр.
Яковлев А.И. Иванова Н.С.
Санкт-Петербург
2008 год
Учебные и воспитательные цели курсовой работы.
В результате выполнения курсовой работы студенты должны:
- углубить, систематизировать и закрепить теоретические знания о способах уравнивания геодезических сетей;
- закрепить основы вероятностно-статистического оценивания и анализа ошибок измерений;
- освоить методику построения математических моделей на ЭВМ;
- совершенствовать навыки по уравниванию геодезических построений на персональных компьютерах;
- научиться обосновывать необходимою точность измерений и умело применять метод статистических испытаний для априорной оценки точности на ЭВМ.
В процессе выполнения курсовой работы воспитывается:
- умение работать самостоятельно с научной и технической литературой;
- уверенность в себе при достижении поставленной цели;
- ответственность за выполнение курсовой работы в намеченные сроки;
- воля, упорство, трудолюбие;
- умение анализировать полученные результаты;
- творческие способности при принятии решений;
- профессиональная гордость.
Задача курсовой работы и основные этапы решения.
В настоящее время резко возрастает количество объектов, требующих геодезической привязки и контроля состояния. Различные схемы привязки и методики контроля вызывают необходимость развития специальных геодезических сетей. Конфигурация геодезической сети и точность ее элементов определяется спецификой объекта. От заданной точности элементов сети зависят методика и оббьем измерений на пункте. Поэтому актуальной становится задача обоснования необходимой точности измерений и допусков, накладываемых на результаты измерений.
Пусть для геодезического обеспечения специального объекта требуется развить сеть триангуляции плотностью 1 пункт на 20 км2 . Точность определения элементов сети mα =6,0”, ms =8 см, где mα – точность ориентирования сторон сети; ms – точность длин сторон сети. Исходная геодезическая сеть характеризуется:
![]() mαисх
=1,5” и msисх
= 1:400 000
mαисх
=1,5” и msисх
= 1:400 000
S
При разработке технических указаний на производство полевых работ требуется рассчитать:
1. Необходимую точность измерений.
2. Число приемов.
3. Требования к приборам и условиям измерений.
4. Допустимые значения невязок геометрических условий.
5. Требования к определению элементов приведения.
Такая задача решается в следующей последовательности:
- моделирование геодезической сети;
- определение корреляционных матриц ошибок дирекционных углов и длин сторон развиваемой сети;
- подбор значения μ(СКО единицы веса), доставляющего требуемую точность дирекционным углам и длинам сторон сети;
- выделение случайной и систематической ошибок, влияющих на значение μ;
- разработка требований к точности прибора и числу приемов;
- установление допусков на разброс измеренных значений и на величину невязок геометрических условий;
- установление необходимой точности учета систематических ошибок;
- установление точности определения элементов приведения.
Моделирование геодезической сети.
Моделирование геодезической сети выполняется на карте масштаба
1:50 000. В заданном районе с требуемой плотностью проектируется сеть триангуляции, и определяются проектные значения координат пунктов. Дирекционные углы и длины сторон вычисляется из решения обратных геодезических задач. Их проектные значения используются в дальнейших вычислениях.
Схема сети:
| |
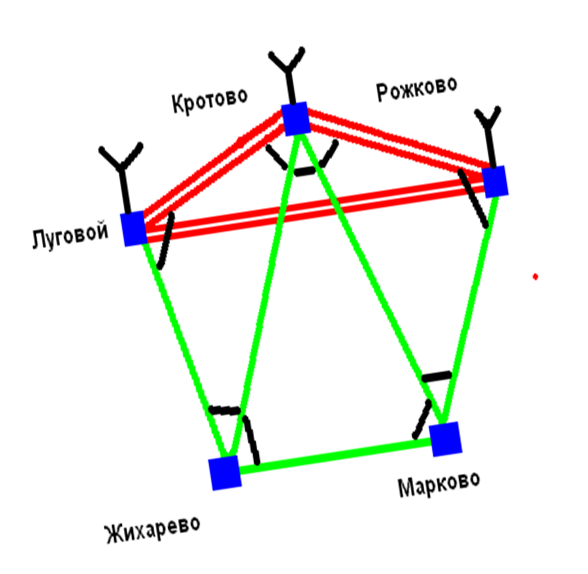
Координаты пунктов данной сети определяются по карте масштаба 1:50 000. Они имеют следующие значения:
Исходные пункты:
| х = |
5 345 777.84 м |
|
| y = |
6 392 520.81 м |
|
| х = |
5 345 712.14 м |
|
| у = |
6 395 188.44 м |
|
| х = |
5 345 462.14 м |
|
| у = |
6 389 068.85 м |
Определяемые пункты:
х=5 342 374.27м
у=6 393 907.75м
х=5 342 287.59м
у=6 390 919.12м
Значения дирекционных углов и длин сторон вычисляются по формулам обратной геодезической задачи:
yj -yi
![]()
![]() α
i
,
j
=arctg xj
-xi
si
,
j
=√(xj
-xi
)2
+(yj
-yi
)2
α
i
,
j
=arctg xj
-xi
si
,
j
=√(xj
-xi
)2
+(yj
-yi
)2
Решение обратных геодезических задач
| 3-4 |
4-5 |
5-1 |
1-2 |
|
| α |
88˚36′22.1″ |
267˚39′12″ |
84˚46′28.3″ |
265º 50’33” |
| s,м |
2668.62 |
3575.86 |
3554.74 |
2996.73 |
| 2-3 |
2-4 |
2-5 |
|
| α |
200º 59’32” |
24˚39′10″ |
20˚59′28″ |
| s,м |
3840.22 |
3520.27 |
3466.37 |
Составление параметрических уравнений поправок направлений.
Параметрические уравнения поправок направлений имеют вид:
![]()
где ![]() — поправка в направление;
— поправка в направление;
![]() — поправка к предварительному значению ориентирующего угла;
— поправка к предварительному значению ориентирующего угла;
![]() — поправки к предварительным значениям координат определяемых пунктов;
— поправки к предварительным значениям координат определяемых пунктов;
а и b — коэффициенты параметрических уравнений поправок, вычисляемые по формулам:
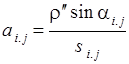 ;
; 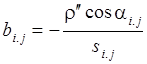 ,
,
где ![]() и
и ![]() —
модельные значения дирекционных углов и длин сторон проектируемой сети;
—
модельные значения дирекционных углов и длин сторон проектируемой сети;
![]() — свободный член уравнения поправок.
— свободный член уравнения поправок.
Параметрические уравнения поправок направлений:
V15 = −δz1 + a51 ξ5 + b51 η5 +l15
V12 = −δz1 + l12
V23 = −δz2 + l23
V24 = −δz2 + a42 ξ4 + b42 η4+ l24
V25 = −δz2 + a52 ξ5 + b52 η5 + l25
V21 = −δz2 + l21
V34 = −δz3 + a43 ξ4 + b43 η4 + l34
V32 = −δz3 + l32
V43 = −δz4 + a43 ξ4 + b43 η4 + l43
V42 = −δz4 + a42 ξ4 + b42 η4 + l42
V45 = −δz4 + a45 ξ4 + b45 η4 + a54 ξ5 + b54 η5 + l45
V51 = −δz5 + a51 ξ5 + b51 η5 + l51
V52 = −δz5 + a52 ξ5 + b52 η5 + l52
V54 = −δz5 + a54 ξ5 + b54 η5 + a45 ξ4 + b45 η4 + l54
Таблица коэффициентов параметрических уравнений поправок
горизонтальных направлений (матрица B
M
):
| Определяемые пункты |
|||||||||||||
| Жихарево |
Марково |
||||||||||||
| Изм. |
|
|
|
|
|
|
|
|
|
||||
| M15 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0,567 |
0,234 |
||||
| M12 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| M23 |
0 |
-1 |
0 |
0 |
0 |
0,463 |
0 |
0 |
0 |
||||
| M24 |
0 |
-1 |
0 |
0 |
0 |
0 |
-0,243 |
0 |
0 |
||||
| M25 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
-0,354 |
-0,479 |
||||
| M21 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| M34 |
0 |
0 |
-1 |
0 |
0 |
0,128 |
-0,345 |
0 |
0 |
||||
| M32 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
||||
| M43 |
0 |
0 |
0 |
-1 |
0 |
-0,057 |
0,468 |
0 |
0 |
||||
| M42 |
0 |
0 |
0 |
-1 |
0 |
0,564 |
0,342 |
0 |
0 |
||||
| M45 |
0 |
0 |
0 |
-1 |
0 |
0,854 |
0,678 |
0,674 |
0,234 |
||||
| M51 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0,682 |
-0,568 |
||||
| M52 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0,335 |
0,435 |
||||
| M54 |
0 |
0 |
0 |
0 |
-0 |
-0,914 |
-0,224 |
-0,463 |
0,866 |
||||
Составление параметрических уравнений поправок измеренных дирекционных углов.
Уравнение поправок дирекционного угла отличается от уравнения поправок направлений тем, что в нем нет поправки в ориентирующий угол. Записывается оно следующим образом:
![]()
Параметрические уравнения поправок измеренных дирекционных углов:
V15 = a51 ξ5 + b51 η5 + l15
V12 = l12
V23 = l23
V24 = a42 ξ4 + b42 η4 + l24
V25 = a52 ξ5 + b52 η5 + l25
V21 = l21
V34 = a43 ξ4 + b43 η4 + l34
V32 =l32
V43 = a43 ξ4 + b43 η4 + l43
V42 = a42 ξ4 + b42 η4 + l42
V45 = a45 ξ4 + b45 η4 + a54 ξ5 + b54 η5 + l45
V51 = a51 ξ5 + b51 η5 + l51
V52 = a52 ξ5 + b52 η5 + l52
V54 = a54 ξ5 + b54 η5 + a45 ξ4 + b45 η4 + l54
Таблица коэффициентов параметрических уравнений поправок
измеренных дирекционных углов (матрица B
a):
| Определяемые пункты |
||||
| Жихарево |
Марково |
|||
|
|
|
|
|
|
| M15 |
0 |
0 |
0,543 |
0,253 |
| M12 |
0 |
0 |
0 |
0 |
| M23 |
0 |
0 |
0 |
0 |
| M24 |
0,401 |
-0,389 |
0 |
0 |
| M25 |
0 |
0 |
0,235 |
0,635 |
| M21 |
0 |
0 |
0 |
0 |
| M34 |
-0,457 |
-0,335 |
0 |
0 |
| M32 |
0 |
0 |
0 |
0 |
| M43 |
0,680 |
0,949 |
0 |
0 |
| M42 |
-0,365 |
0,35 |
0 |
0 |
| M45 |
-0,765 |
0,206 |
-0,831 |
0,206 |
| M51 |
0 |
0 |
-0,442 |
-0,254 |
| M52 |
0 |
0 |
-0,216 |
0,968 |
| M54 |
0,765 |
-0,345 |
0,765 |
-0,345 |
Составление параметрических уравнений
поправок измеренных длин сторон.
В проектируемой сети могут планироваться измерения отдельных длин сторон. Параметрическое уравнение поправок стороны имеет вид: ![]()
где с и d — коэффициенты уравнений, вычисляемые по формулам
![]() ,
,
а l - исключаемая постоянная систематическая ошибка, обусловленная разностью уровней принимаемых сигналов при проведении измерений и определении поправок.
Параметрические уравнения поправок измеренных длин сторон:
VS 51 = c15 ξ5 + d15 η5 + l51 = cosα15 ξ5 + sinα15 η5 + l15
VS 52 = c25 ξ5 + d25 η5 + l25 = cosα25 ξ5 + sinα25 η5 + l25
VS 42 = c24 ξ4 + d24 η4 + l24 = cosα24 ξ4 + sinα24 η5 + l24
VS 43 = c34 ξ4 + d34 η4 + l34 = cosα34 ξ4 + sinα34 η4 + l34
VS 35 = c35 ξ5 + d35 η5 + l35 = cosα35 ξ5 + sinα35 η5 + l35
VS 45 = c45 ξ4 + d45 η4 + c54 ξ5 + d54 η5 + l45 = −cosα45 ξ4 − sinα45 η4 + cosα45 ξ5 + sinα45 η5 + l45
Таблица коэффициентов параметрических уравнений поправок
измеренных длин сторон (матрица B
s
):
| Определяемые пункты |
||||
| Изм. |
Скочково |
Лесное |
||
|
|
|
|
|
|
| S5 1 |
0 |
0 |
-0,4981 |
-0,8671 29-04-2015, 00:33 Разделы сайта |
