S5 2
0
0
0,9761
-0,2175
S4 2
0,6828
-0,7306
0
0
S4 3
0,9833
0,1818
0
0
S45
0,2405
-0,9706
-0,2405
0,9706
Установление единицы веса и вычисление исходной весовой матрицы P для уравниваемых величин.
Измеряемые углы на пунктах триангуляции представляются рядом равноточных независимых направлений. Поэтому в качестве единицы веса целесообразно взять вес измерения направлений. Тогда корреляционная матрица ошибок направлений, а следовательно, и ее весовая матрица PМ , будут равны единичной матрице
Q = PМ = Е .
Вычисление корреляционной матрицы ошибок координат определяемых пунктов.
Корреляционная матрица ошибок необходимых параметров равна обратной матрице коэффициентов нормальных уравнений
![]() .
.
Благодаря диагональной конструкции матрицы P формулу для вычисления коэффициентов нормальных уравнений представим в виде

Учитывая, что ![]() и в рассматриваемой сети не планируются измерения азимутов и длин сторон, корреляционная матрица ошибок необходимых параметров будет равна
и в рассматриваемой сети не планируются измерения азимутов и длин сторон, корреляционная матрица ошибок необходимых параметров будет равна
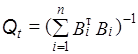 .
.
В результате вычислений получим:
![]() =
=
| 0,7547 |
-0,0536 |
0,0224 |
0,0522 |
-0,0639 |
-0,3958 |
0,0593 |
0,4551 |
0,1392 |
| -0,0536 |
0,3158 |
0,0566 |
-0,128 |
0,0382 |
0,2224 |
-0,166 |
-0,1546 |
-0,1527 |
| 0,0064 |
0,0566 |
0,7559 |
-0,2869 |
0,0368 |
-0,0061 |
-0,5632 |
0,0366 |
-0,0135 |
| 0,0522 |
-0,128 |
-0,2869 |
0,8841 |
-0,2239 |
-0,677 |
0,7581 |
0,2277 |
0,0151 |
| -0,0639 |
0,0382 |
0,0368 |
-0,2239 |
0,5244 |
0,6486 |
-0,2013 |
-0,3494 |
0,1048 |
| -0,3958 |
0,2224 |
-0,0061 |
-0,677 |
0,6486 |
2,6272 |
-0,4731 |
-1,756 |
-0,061 |
| 0,0593 |
-0,166 |
-0,5632 |
0,7581 |
-0,2013 |
-0,4731 |
1,3295 |
0,2446 |
0,0412 |
| 0,4551 |
-0,1546 |
0,0366 |
0,2277 |
-0,3494 |
-1,756 |
0,2446 |
1,9114 |
0,2573 |
| 0,1392 |
-0,1527 |
-0,0135 |
0,0151 |
0,1048 |
-0,061 |
0,0412 |
0,2573 |
0,648 |
матрицу ![]() можно разбить на блоки
можно разбить на блоки 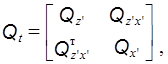
где ![]() — корреляционная матрица ошибок уравненных значений ориентирующих углов;
— корреляционная матрица ошибок уравненных значений ориентирующих углов;
![]() —матрица взаимных весовых коэффициентов между уравненными значениями ориентирующих углов и уравненными значениями координат определяемых пунктов;
—матрица взаимных весовых коэффициентов между уравненными значениями ориентирующих углов и уравненными значениями координат определяемых пунктов;
![]() — корреляционная матрица ошибок координат определяемых пунктов.
— корреляционная матрица ошибок координат определяемых пунктов.
| 3,5788 |
-0,4731 |
-1,756 |
-0,061 |
| -0,4731 |
2,3295 |
0,2446 |
0,0412 |
| -1,756 |
0,2446 |
2,9114 |
0,2573 |
| -0,061 |
0,0412 |
0,2573 |
2,648 |
![]()
![]() x=
x=
Вычисление корреляционных матриц ошибок
дирекционных углов и длин сторон сети.
Дирекционные углы и длины сторон геодезической сети являются функциями координат:
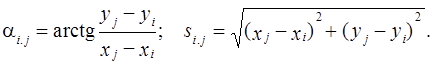
Корреляционные матрицы их ошибок в уравненной сети вычисляются по формулам:
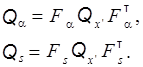
F a — матрица частных производных оцениваемых дирекционных углов;
Fs — матрица частных производных оцениваемых длин сторон сети.
Известно, что
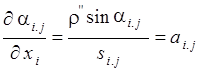 ,
, 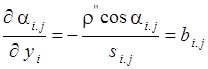
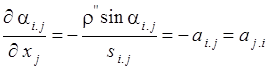 ,
, 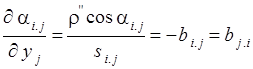 ,
,
где ![]() и
и ![]() —
модельные значения дирекционных углов и длин сторон проектируемой сети.
—
модельные значения дирекционных углов и длин сторон проектируемой сети.
Производные ![]() ,
, ![]() ,
, ![]() и
и ![]() равны
равны
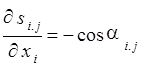 ,
, 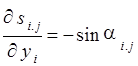
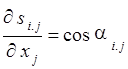 ,
, 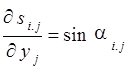 .
.
| Определяемые пункты |
||||
| Изм. |
Жихарево |
Марково |
||
|
|
|
|
|
|
| a51 |
0, |
0 |
-0,4235 |
-07546 |
| a52 |
0 |
0 |
0,3428 |
-0,3426 |
| a43 |
0,5678 |
-0,5673 |
0 |
0 |
| a42 |
09734 |
0,4536 |
0 |
0 |
| a45 |
0,4632 |
-0,4256 |
-0,2533 |
0,3527 |
Матрица частных производных оцениваемых
дирекционных углов (матрица F a ):
Матрица частных производных оцениваемых
длин сторон (матрица Fs ):
| Определяемые пункты |
||||
| Изм. |
Жихарево |
Марково |
||
|
|
|
|
|
|
| S 51 |
0 |
0 |
-34,25 |
-35,43 |
| S 52 |
0 |
0 |
-23.44 |
76,38 |
| S42 |
45,45 |
37,54 |
0 |
0 |
| S43 |
23,45 |
43,26 |
0 |
0 |
| S45 |
-64,53 |
54,16 |
-34.56 |
32,34 |
После перемножения матриц ![]() получим искомую корреляционную матрицу ошибок дирекционных углов
получим искомую корреляционную матрицу ошибок дирекционных углов ![]() :
:
| 0,5414 |
0,3007 |
-0,1319 |
-0,02 |
0,1519 |
| 0,3007 |
0,628 |
0,1568 |
0,0782 |
-0,235 |
| -0,1319 |
0,1568 |
0,6979 |
0,1815 |
0,1206 |
| -0,02 |
0,0782 |
0,1815 |
0,7445 |
0,074 |
| 0,1519 |
-0,235 |
0,1206 |
0,074 |
0,8055 |
После перемножения матриц ![]() получим корреляционную матрицу ошибок длин сторон
получим корреляционную матрицу ошибок длин сторон ![]() :
:
| 0,557835 |
0,007676 |
-0,002272 |
-0,004542 |
0,001327 |
| 0,007676 |
0,000300 |
-0,000057 |
-0,000205 |
0,000009 |
| -0,002272 |
-0,000057 |
0,000135 |
0,000033 |
0,000002 |
| -0,004542 |
-0,000205 |
0,000033 |
0,000212 |
0,000009 |
| 0,001327 |
0,000009 |
0,000002 |
0,000009 |
0,000062 |
Определение средней квадратической ошибки единицы веса .
Имея заданную точность определения дирекционных углов и длин сторон сети, а также корреляционные матрицы их ошибок ![]() и
и ![]() можно подобрать такое максимальное значение m,
которое доставит определяемым величинам заданную точность. Для этого в корреляционных матрицах
можно подобрать такое максимальное значение m,
которое доставит определяемым величинам заданную точность. Для этого в корреляционных матрицах ![]() и
и ![]() выбираются максимальные диагональные элементы. Заметим, что диагональные элементы этих матриц равны обратным весам оцениваемых дирекционных углов и длин сторон сети.
выбираются максимальные диагональные элементы. Заметим, что диагональные элементы этих матриц равны обратным весам оцениваемых дирекционных углов и длин сторон сети.
По формулам:
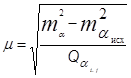 ;
; 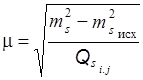
вычисляются значения средней квадратической ошибки единицы веса.
Из двух значений m выбирается наименьшее значение. В этих формулах ![]() и
и ![]() означают требуемые точности определения дирекционных углов и длин сторон сети.
означают требуемые точности определения дирекционных углов и длин сторон сети.
Для данной сети имеем:
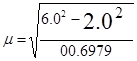 =6,77˝
=6,77˝
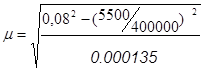 =6,78˝
=6,78˝
для средней квадратической ошибки единицы веса необходимо установить значение равное 6,78". Оно является максимально возможным из всех, которые могут доставить дирекционным углам и длинам сторон проектируемой сети требуемую точность.
Определение случайной и систематической
средних квадратических ошибок измерений .
За единицу веса принят вес измерения направлений. Известно, что угловые измерения сопровождаются случайными и систематическими ошибками. Поэтому среднюю квадратическую ошибку единицы веса представим в виде:
![]() ,
,
где m D - средняя квадратическая случайная ошибка измерения направлений;
m d - средняя квадратическая систематическая ошибка измерения направлений.
Влияние случайных ошибок ослабляется путем увеличения числа приемов. По экономическим соображениям число приемов ограничивается и доводится до определенного минимума, который позволяет свести случайные ошибки к пренебрегаемым величинам. Если ![]() , то влияние случайных ошибок на результаты измерений будет незначительным по сравнению с влиянием систематических ошибок. Определим случайную составляющую средней квадратической ошибки единицы веса. Для этого примем
, то влияние случайных ошибок на результаты измерений будет незначительным по сравнению с влиянием систематических ошибок. Определим случайную составляющую средней квадратической ошибки единицы веса. Для этого примем ![]() . Тогда:
. Тогда:
![]() .
.
Отсюда находим:
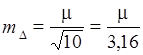 .
.
В развиваемой сети случайная составляющая средней квадратической ошибки единицы веса должна быть равной:
|
|
Влияние систематических ошибок на точность измерений горизонтальных направлений в рассматриваемой сети не должно превосходить:
![]()
Требования к точности прибора и числу приемов.
Величина ![]() определяет, с какой средней квадратической случайной ошибкой должны быть получены в результате многократных измерений элементы геодезической сети. Она позволяет установить для них предельные ошибки
определяет, с какой средней квадратической случайной ошибкой должны быть получены в результате многократных измерений элементы геодезической сети. Она позволяет установить для них предельные ошибки![]() . Для установления значения
. Для установления значения ![]() обычно назначают вероятности выполнения неравенства
обычно назначают вероятности выполнения неравенства
![]()
равными:
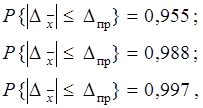
где ![]() — случайная ошибка среднего арифметического значения измеряемой величины.
— случайная ошибка среднего арифметического значения измеряемой величины.
Тогда предельные ошибки будут равны:
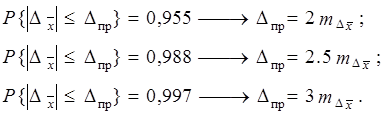
Предельные ошибки при проектировании измерений, как правило, определяются по формуле:
![]() .
.
Проектируемая сеть является сетью триангуляции. Значения горизонтальных направлений на пунктах триангуляции могут быть получены в результате измерения горизонтальных углов способом круговых приемов (способ Струве) и способом во всех комбинациях (способ Шрейбера). Предельные ошибки значений горизонтальных углов, полученных в результате многократных измерений будут равны:
![]() ,
,
где ![]() — проектное значение средней квадратической случайной ошибки измерения горизонтальных углов.
— проектное значение средней квадратической случайной ошибки измерения горизонтальных углов.
Горизонтальные углы являются функциями равноточных направлений. Поэтому для рассматриваемой сети будем иметь:
|
|
предельная ошибка измерения горизонтальных углов составит:
|
|
Для обоснования требований к точности прибора и числу приемов рассмотрим величину:
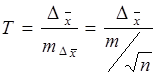 ,
,
где m — средняя квадратическая случайная ошибка измерений одним приемом, вычисляемая по результатам измерений (по формуле Бесселя).
Величина T
является случайной. Она имеет распределение Стьюдента. Функция распределения по закону Стьюдента выражает вероятность того, что случайная величина T
принимает по абсолютной величине значения меньшие заданного ![]()
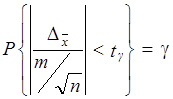 .
.
Распределение Стьюдента зависит от числа степеней свободы r . Для измеряемых величин число степеней свободы определяется по формуле:
r = n – 1 ,
где n — количество приемов.
Приняв определенное значение g и задавая степень свободы r
по таблице Стьюдента можно найти ![]() . Ему должна соответствовать величина:
. Ему должна соответствовать величина:
. 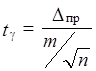
Отсюда следует:
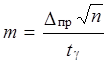 .
.
Степень свободы подбирается такой, чтобы точность измерения одним приемом m и число приемов n = r + 1 были приемлемы при производстве наблюдений на пунктах сети.
По величине m определяется класс прибора, обеспечивающий данную точность измерений одним приемом:
m п < m ,
где m п — паспортное значение средней квадратической ошибки измерения одним приемом.
Значение g должно назначаться примерно равным единице. Если взять, например, g = 0,9 — то в десяти случаях из ста могут оказаться незамеченными измерения, для которых случайная ошибка среднего арифметического значения будет больше предельной, т.е. 10% некачественных измерений будут приняты в обработку. При g = 0,99 только 1% некачественных измерений будет незамеченным. Обычно g принимается равным 0,995; 0,997; 0,999.
Примем g = 0,999. По таблице распределения Стьюдента для r
= 2 находим ![]() = 31.6. Из выражения r = n
– 1 определяем число приемов
= 31.6. Из выражения r = n
– 1 определяем число приемов
n = r + 1 = 3.
Среднюю квадратическую ошибку измерения угла одним приемом вычислим по формуле
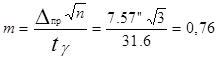 .
.
Таким образом, чтобы получить значения горизонтальных углов с
29-04-2015, 00:33

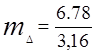 =2,14
=2,14