![]() (21)
(21)
![]() (22)
(22)
Формула (22) выражает величину единичного притока с одной стороны дрены. Для получения полного притока воды в дрену необходимо умножить единичный приток на два, а затем — на длину дрены. Приток воды в торцы дрены обычно не учитывают, так как он при большой длине дрены составляет ничтожную долю.
По формуле (22) можно рассчитать расход плоского грунтового потока. Подставив вместо радиуса влияния расстояние между сечениями, равное I , получим
![]() (23)
(23)
Выражение ![]() можно записать так
можно записать так
![]() (24)
(24)
т. е. единичный расход равен
![]() (25)
(25)
а полный расход составит
![]() (26)
(26)
Исследуя выражение (22), мы сможем решить одну из весьма важных задач в гидрогеологических расчетах — вывести уравнение депрессионной кривой. Построение депрессионной кривой необходимо при возникновении угрозы затопления подземными водами котлованов, подвалов зданий и т. п..
Изменив пределы интегрирования в выражении (20) по X от 0 до х, а по У от h0 до h К получим
![]() (27)
(27)
Естественно, что приток воды в выражениях (22) и (27) одинаков, т. е.
![]() (28)
(28)
Решаем (28) относительно h
![]() (29)
(29)
Для построения депрессионной кривой мы задаемся величиной hо в зависимости от 5, мощность водоносного горизонта H легко получить по данным бурения, величину радиуса влияния можно найти по эмпирическим формулам (об этом мы поговорим позже).
На миллиметровой бумаге строим разрез через дрену и котлован (рис. 52) и, задаваясь разными значениями х(хи x2 ,. .., хп ), например 10, 20, 30 и т. д. метров, получаем величины h(h, h2 ,..., hп ). Соединив полученные точки плавной линией, получим кривую депрессии. Если она проходит через котлован, строят новую кривую, задавшись большей величиной понижения и, естественно, меньшим значением глубины воды в дрене. Построение производят до тех пор, пока депрессионная кривая не опустится ниже дна котлована.
4.2 Расчет притока грунтовых вод в скважину
Здесь мы имеем дело не с плоским потоком, как в предыдущем примере, а с радиальным. На рис. 10 показаны все обозначения, которые нам ясны из предыдущей задачи, кроме г — радиуса скважины.
Расчет начинаем с уравнения (13). Площадь притока воды равна площади боковой поверхности цилиндра, радиус которого равен х, т. е.
![]() (30)
(30)
![]() (31)
(31)
Разделяем переменные (т. е. умножаем обе части уравнения на ![]() ) и интегрируем
) и интегрируем
 (32)
(32)
Интегрирование по х производим не от нуля, а от r — стенки скважины, в результате получаем формулу Дюпюи
![]() (33)
(33)
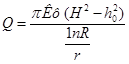 (34)
(34)
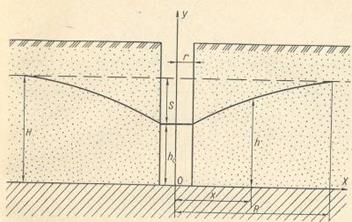
Рис. 2. Схема притока грунтовых вод в совершенную скважину
В таком виде использовать выражение (2) не совсем удобно, так как в нем присутствует натуральный логарифм. Подставим вместо него десятичный (1nх = 2,30 lgх), а вместо л его значение и получим более удобное выражение для расчета притока безнапорных вод в скважину:
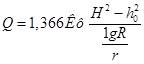 (35)
(35)
Выражение ![]() можно видоизменить:
можно видоизменить:
![]() (36)
(36)
И, подставив его в зависимость 54), получим
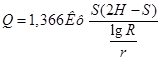 (37)
(37)
Для построения депрессионной кривой возвращаемся к (35) и изменяем пределы интегрирования: по X от r до х а по Y от h0 до h:
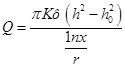 (38)
(38)
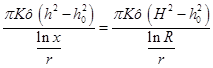 (39)
(39)
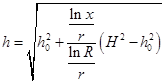 (40)
(40)
Решаем равенство относительно h и получаем уравнение кривой депрессии
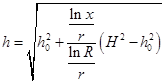 (41)
(41)
4.3 Расчет притока напорных вод в совершенную дрену
Площадь фильтрации в сечении h, расположенном на расстоянии х от стенки дрены, будет равна
![]() (42)
(42)
Мы здесь снова не учитываем приток воды через торцы дрены. Подставляем площадь в (43):
![]() (43)
(43)
Переходим к единичному расходу
![]() (44)
(44)
Разделяя переменные и интегрируя, получим
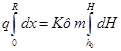 (45)
(45)
![]() (46)
(46)
![]() (47)
(47)
Выражение (47) представляет собой единичный приток артезианских вод в один из бортов канавы. Полный приток составит
![]() (48)
(48)
Если нам необходимо получить уравнение депрессионной кривой, то (43) нужно проинтегрировать по Х от 0 до ж, а по Y от hо до h:
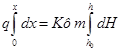 (49)
(49)
![]() (50)
(50)
![]() (51)
(51)
Решаем уравнение (51) относительно h:
![]() (52)
(52)
Анализируя выражение (52), мы видим, что это уравнение прямой линии. На самом деле депрессионная кривая криволинейна.
4.4 Расчет притока артезианских вод в скважину
В выражение (14) подставляем величину площади фильтрации, которая равна
![]() (53)
(53)
![]() (54)
(54)
Разделяя переменные и интегрируя по X от r до Н, а по Y от hо до Н, получим
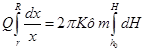 (55)
(55)
![]() (56)
(56)
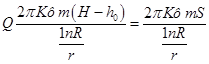 (57)
(57)
Переведем натуральный логарифм в десятичный и подставим значение я. Получим выражение для расчета притока артезианских вод в совершенную скважину:
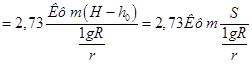 (58)
(58)
Для расчета кривой депрессии возвратимся к (55) и сменим пределы интегрирования: по X от r до х, а по Y от hо до h:
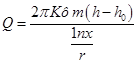 (59)
(59)
Выражения (57) и (59) равны:
 (60)
(60)
Находим h:
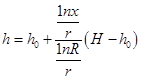 (61)
(61)
т. е. мы снова имеем уравнение прямой линии, хотя в природных условиях депрессионная воронка в разрезе имеет вид кривой.
Все вышеприведенные формулы крайне просты и могут служить лишь для приблизительных расчетов. В гидрогеологической практике применяются формулы, учитывающие уклоны водоупоров, неоднородность в водопроницаемости слоев, поправки на несовершенство скважин, на неустановившееся движение и т. д.
Понятие о дебите и удельном дебите.
Дебит (по-фр.— сбыт, расход) — количество воды, нефти, газа, даваемое источником, колодцем, скважиной за единицу времени. Единицами измерения дебита для подземных вод являются м3 /с или м3 /сут, для нефти — т/сут. Удельный дебит получают при делении величины дебита на величину понижения уровня
![]() (62)
(62)
и обычно измеряют м2 /сут.
5. Методы определения коэффициента фильтрации горных пород. Определение радиуса влияния
Как видно из приведенных в предыдущем параграфе формул, в большинстве из них присутствуют величины коэффициента фильтрации и радиуса влияния, на методах определения которых мы и остановимся.
Определение коэффициента фильтрации горных пород можно проводить на основании использования эмпирических формул, лабораторных данных и полевых опытов.
Эмпирические формулы позволяют быстро определить коэффициент фильтрации горных пород на основании данных об их пористости и механического состава. Однако эти формулы дают лишь приблизительные представления о водопроницаемости пород и могут быть использованы только при предварительных расчетах.
Для определения коэффициента фильтрации песков с эффективным диаметром частиц, равным от 0,1 до 3,0 мм, и при коэффициенте неоднородности менее 5,0 можно применять формулу Хазена
![]() , м/сут, (63)
, м/сут, (63)
где С—эмпирический коэффициент, равный, по О. К. Ла-нге,
![]() (64)
(64)
п — пористость породы, %; dэ ~ эффективный диаметр частиц, мм; t° — температура воды, °С.
Для определения эффективного диаметра и коэффициента-неоднородности необходимо построить интегральную (суммарную) кривую механического состава. Обычно результаты анализов механического состава лаборатория выдает в виде стандартной таблицы (табл. 1). Для построения суммарной кривой необходимо знать суммарные содержания фракций диаметром менее 0,005; 0,01; 0,05; 0,1; 0,25 и т. д. мм. Для этого в таблице справа налево мы суммируем содержания фракций и записываем ниже (под содержанием фракций, %).
| Характеристики | Размер частиц, мм | ||||||||
| > 2,0 | 2,0-1,0 | 1,0-0,5 | 0,5-0,25 | 0,25-0,1 | 0,1-0,05 | 0,05-0,01 | 0,01-0,005 | < 0,005 | |
| Содержание фракций, % | 3,5 | 6,2 | 20,3 | 35,2 | 26,2 | 4,5 | 2,8 | 0,5 | 0,7 |
| Суммарное содержание фракций, % | 100,0 | 96,4 | 90,2 | 69,9 | 34,7 | 8,5 | 4,0 | 1,2 | 0,7 |
Таблица 1. Данные для построения суммарной кривой механического состава породы
На графике по оси абсцисс откладываем логарифмы диаметра частиц, по оси ординат — суммарное содержание, %.
После построения кривой находим величины эффективного и контролирующего (dк ) диаметров, т. е. размеры частиц, меньше которых в породе содержится 10 и 60 %. В нашем примере dэ = 0,11 мм, dк = 0,42 мм. Теперь можно найти коэффициент неоднородности Кн
![]() (65)
(65)
Наряду с (81) можно применять и формулу Козени
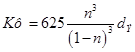 (66)
(66)
где п — пористость в долях от единицы.
В лабораторных условиях чаще всего применяют трубку Спецгео и трубку КФЗ конструкции Д. И. Знаменского.
Трубка Спецгео конструкции Е. В. Симонова состоит из основной трубки 1, нижней крышки 2 с сеткой, верхней сетки 3, верхней крышки 4 и стеклянного мерного цилиндра 5, снабженного шкалой с делениями через 10 см3 . Мерный цилиндр поддерживает постоянный уровень над верхней сеткой, так как из него выливается вода только после поступления внутрь пузырьков воздуха. Этим достигается и постоянство гидравлического градиента, равного единице (напор равен пути фильтрации).
Коэффициент фильтрации вычисляют по формуле
![]() (67)
(67)
где Q — расход воды, см3 /с; F — площадь поперечного сечения трубки, равная 28 см2 ; V — объем профильтровавшейся воды, см3 ; t — время, с; t° - температура воды, °С.
Полевые опыты проводятся в полевых (натурных) условиях и дают наиболее надежные данные о фильтрационных свойствах пород. Полевые опыты заключаются в производстве откачек или наливов воды в скважины и шурфы.
Откачки проводят при неглубоком залегании подземных вод. На участке, где предполагается изучать водопроводимость пород, закладывают одну или несколько скважин на водоносный горизонт и откачивают воду. В результате уровень подземных вод понижается и вокруг скважины образуется депрессионная воронка. Как мы видели выше, дебит скважины зависит от коэффициента фильтрации, величины понижения уровня подземных вод и радиуса влияния. Определив при откачке дебит, динамический уровень и радиус влияния, можно получить коэффициент фильтрации.
Откачки бывают одиночные и кустовые. Одиночные откачки производят из одной скважины без наблюдения за депрессионной воронкой. При кустовых откачках бурят группу (куст) скважин, из которых одна центральная является опытной (из нее ведут откачку воды), а остальные служат для наблюдения за распространением воронки депрессии вокруг центральной скважины. Наблюдательные скважины в кустах располагаются по одному или 2—4 лучам, отходящим от центральной скважины. Необходимо, чтобы один из лучей совпадал с направлением движения подземного потока. На каждом из лучей закладывают не менее двух наблюдательных скважин.
Величина коэффициента фильтрации, полученная по данным опытной откачки, является средней для всей толщи породы, охваченной опытным кустом.
Для определения коэффициента фильтрации по данным одиночным откачкам пользуются формулами, по которым вычисляют приток воды к колодцам и скважинам (35) и (58), решив их относительно Кф. При этом радиус влияния можно принять для песков крупных — равным 500 м, для песков средней крупности — 150—100 м, для песков мелких — 75—50 м, для песков пылеватых и супесей— 30—20 м. Небольшая неточность в определении радиуса влияния не окажет большого влияния на расчет, так как этот параметр входит в формулу под знаком логарифма.
Коэффициент фильтрации вычисляется по следующим формулам:.
а) для безнапорных вод
![]() (68)
(68)
б) для напорных вод
![]() (69)
(69)
При наличии двух наблюдательных скважин коэффициент фильтрации определяется по формулам:
а) для безнапорных вод на участке центральная (ц) — первая наблюдательная (1н) скважины
![]() (70)
(70)
на участке между наблюдательными скважинами
![]() (71)
(71)
Получив два значения коэффициента фильтрации, из них находят среднюю величину, принимая ее за истинную. Иногда определяют еще и третье значение коэффициента фильтрации — в промежутке центральная — вторая наблюдательная скважины.
б) для артезианских вод определение ведется аналогичным путем:
![]() (72)
(72)
![]() (73)
(73)
Обычно опытные откачки производят при нескольких понижениях уровня.
При глубоком залегании подземных вод рациональнее вместо откачек производить нагнетание воды в скважины или наливы ее в шурфы.
При опытных нагнетаниях в скважине, а также на некотором расстоянии от нее уровни подземных вод повышаются. Зная расход воды при нагнетании и величину повышения уровня в опытной и наблюдательной скважиных, можно вычислить коэффициент фильтрации по тем же формулам, что и для опытных откачек, подставив в формулы вместо величины понижений соответствующие величины повышения уровня.
Налив воды в шурф по способу Болдырева применяют для определения водопроницаемости верхних слоев пород. Воду в шурф подают в таком количестве, чтобы над дном поддерживался ее слой толщиной около 10 см. Объем профильтровавшейся воды разделяют на время и получают расход. Далее коэффициент фильтрации находят по формуле
![]() (74)
(74)
где Q — расход, м3 /сут; F — площадь поперечного сечения шурфа, м2 .
Более точные результаты дает способ, основанный на применении прибора ПВН (прибор водопроницаемости Нестерова). Прибор состоит из двух колец, которые вдавливаются в испытываемую породу в дне шурфа или закопушки (закопушка — горная выработка, предназначенная для вскрытия коренных пород, залегающих непосредственно под почвенно-растительным слоем, обычно имеет глубину до 0,5 м). Прибор ПВН применяется для определения коэффициента фильтрации слабопроницаемых пород (супесей, суглинков). Как видно из рис. 14, б, инфильтрация по краям потока расходится в виде веера и мы не можем точно определить площадь фильтрации. В центральной части потока вода фильтруется вертикально. Предполагается, что поперечное сечение инфильтрационного потока из внутреннего кольца равно его площади. Поддерживая слои воды в обоих кольцах одинаковыми, определяем установившийся расход из бачка, питающего инфильтрацию из внутреннего кольца.
Расчет коэффициента фильтрации ведем по зависимости
![]() (75)
(75)
где Q — величина установившегося расхода, м3 /сут; F — площадь внутреннего кольца, м2 ; Нк — высота капиллярного поднятия, м; h— высота слоя воды в кольцах, м; l — глубина просачивания воды, м, определяемая бурением после окончания опыта.
Определение радиуса влияния производят на основании эмпирических формул и полевых опытов.
Среди эмпирических формул наиболее часто применяются зависимости И.П. Кусакина:
для безнапорных вод
![]() , м (76)
, м (76)
для напорных вод
![]() , м (77)
, м (77)
Определение радиуса влияния на основании опытных откачек ведут аналитическим или графическим способом. Аналитически — из выражений (56) и (76), решая их относительно R.
Графический способ понятен из рис. 13. По данным откачки в масштабе строят разрез и продолжают (экстраполируют) депрессионную кривую за пределами крайней наблюдательной скважины.
Измерив расстояние от центральной скважины до R, получают величину радиуса влияния.
Заключение
Динамика подземных вод - отрасль гидрогеологии, рассматривающая теоретические основы и методы изучения количественных закономерностей режима и баланса подземных вод. С точки зрения методологических построений, основывающихся на теории фильтрации, неразрывно связана с гидравликой и гидромеханикой.
Многие положения динамики грунтовых вод., касающиеся главным образом гидромеханических проблем, заложены во 2-й половине 19 — начале 20 вв. исследователями, работавшими в области гидравлики и теоретической механики, — французскими учёными Д. Дарси и Ж. Дюпюи, установившими линейный закон фильтрации, русским учёным Н. Е. Жуковским, работавшим над теорией движения подземных вод, и др. Современные основы теории и методики Д. п. в. созданы преимущественно работами советских учёных, проведёнными в 20—30-х гг. 20 в. в связи с решением задач гидротехнического строительства. Н.Н. Павловский разработал проблемы динамики грунтовых вод в связи с гидротехническим строительством, Г.Н. Каменский — проблемы связи динамики подземных вод с геологическими условиями, вопросы движения грунтовых вод в неоднородных пластах, методику расчёта подпоров грунтовых вод и др. Для развития Д. п. в. большое значение имеет разработка вопросов нефтяной подземной гидравлики (газогидродинамика), заложенной в СССР работами Л.С. Лейбензона.
В современный период характерно активное применение гидродинамических расчётов почти во всех гидрогеологических исследованиях. Завершена разработка методики расчётов стационарной фильтрации и разработаны теоретические основы прогнозов подпора грунтовых вод в районах гидросооружений и орошаемых территорий; обосновываются методы оценки эксплуатационных запасов подземных вод; сформулированы основные направления исследований региональной динамики глубоких и взаимодействующих водоносных горизонтов.
Воздействие хозяйственной деятельности человека на подземные воды приводит к необходимости рассмотрения сложных расчётных схем, поэтому, помимо аналитических методов расчёта, широко используются методы математического моделирования с применением аналоговых приборов и цифровых ЭВМ. Это позволяет проводить гидрогеологические расчёты с возможно более полным учётом природной обстановки и всех действующих факторов. Для решения стационарных задач, как правило, используют сплошные электрические модели из электропроводной бумаги, а для решения нестационарных задач — гидроинтеграторы и сеточные электроинтеграторы на активных сопротивлениях (сетка Либманна) и на активных сопротивлениях с ёмкостями (сетка R — С).
Наряду с решением прямых гидрогеодинамических задач, в которых даётся прогноз режима и баланса подземных вод, в Д. п. в. рассматриваются решения обратных задач — восстановление параметров фильтрационной схемы по данным о режиме подземных вод (например, при многолетней работе крупных водозаборов подземных вод, в районах водохранилищ, карьеров).
29-04-2015, 00:43
