На практике не существует резких границ перехода между структурами ГЖС, здесь могут образовываться переходные структуры. Возникновение различных структур потока ГЖС зависит от вязкости нефти, наличия в ней ПАВ, способствующих распылению газа в потоке.
Знание различных структур потока ГЖС необходим для расчетов движения потоков в вертикальной трубе.
Лекция №5
Гидродинамический расчет процесса движения ГЖС в вертикальной трубе
скважина гидродинамический газ фонтанный
Расчет подъемника заключается в определении распределения давления по стволу работающей скважины, диаметра подъемника, глубины его спуска и пропускной способности.
Рассмотрим 2 случая работы скважины – добычу маловязкой и высоковязкой нефти. Здесь основные отличия заключаются в следующем:
1) потери на трение при подъеме высоковязкой нефти играют существенную роль в общем балансе энергии, тогда как потери на трение при подъеме маловязкой нефти достаточно малы;
2) структура потока и режим движения ГЖС в подъемнике при подъеме высоковязкой нефти обычно остаются постоянными, т.е. эмульсионная структура при ламинарном режиме;
3) скольжение фаз (относительная скорость газа в нефти) пренебрежимо мало.
При расчете распределения давления по стволу скважины необходимо учитывать различные структуры потока ГЖС, которым соответствуют различные схемы для определения гидравлических характеристик потока. Изменение структуры потока играет существенную роль в скважинах с маловязкой нефтью.
При подъеме маловязкой нефти потери на трение составляют незначительную долю перепада давления между забоем и устьем скважины (примерно ≈ 0,6 – 1%).
Структура потока по глубине может изменяться, в нижней части НКТ обычно имеет место эмульсионная структура, который выше может переходить в четочную структуру и т.д. Граница перехода одного режима в другой четко не определяется, что снижает точность расчетов.
Таким образом, расчет перепада давления по стволу скважины при движении ГЖС сводится к расчету гидростатического давления. Для этого необходимо знать, как изменяется удельный вес ГЖС по глубине: γсм = γсм (h).
Поскольку γсм = γж (1 - φ) + γг · φ,
где γж, γг – удельный вес соответственно жидкости и газа; φ – объемная концентрация газа в данном сечении.
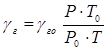
удельный вес газа, приведенный к условиям Р и Т.
В практических условиях объемное газосодержание φ не определяют. Удобной для измерения величиной является расходное газосодержание – отношение расхода газа к сумме расходов газа и жидкости.
Зная зависимость γсм (h), интегрированием уравнения
находят распределение давления по глубине.
При известном давлении на устье Ру формула имеет следующий вид:
,
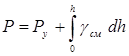где h – глубина скважины.
При известном забойном давлении Рз
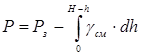
где Н – глубина скважины.
При определении расходного газосодержания следует учитывать как свободный газ, поступающий в скважину из пласта, или газ, закачиваемый в скважину при газлифтном способе эксплуатации, так и газ, выделяющийся из нефти при подъеме жидкости вверх. Обозначим массовый дебит свободного газа через qгс. Примем линейный закон растворимости газа в нефти (закон Генри) и рассмотрим участок подъемника длиной dh. Изменение qг на этом участке происходит за счет выделения газа из нефти, т. е. баланс массы газа за время dt будет:
где а – коэффициент Генри; ρго – плотность газа при нормальных условиях; F – площадь поперечного сечения труб.
Δq2 = q2 (h + dh) – q (h)
Δp = p (h) – p (h + dh)
Учтем, что dh = υж · dt, тогда получим:
где υж – скорость движения жидкости в трубах.
Расходное газосодержание
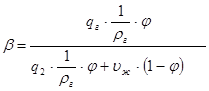
Очевидно, что υж · (1 - φ) · F = Q,
где Q – дебит скважины
Зная зависимость φ = φ (β) находим распределение давления по стволу скважины Р, объемное газосодержание φ и дебит газа qг.
Теперь рассмотрим особенности расчета подъемника высоковязкой жидкости. В этом случае необходимо учесть потери давления на трение, т.е.:
где 
- скорость движения смеси;
λсм – коэффициент гидравлического сопротивления смеси.
λсм можно оценить по формуле λсм ≈ λж; при ламинарном движении потока 
. При высокой вязкости откачиваемой жидкости необходимо учитывать изменение температуры потока по глубине, т.к. вязкость очень сильно зависит от температуры. Распределение температуры по глубине можно определить опытным путем или расчетным.
Рассмотрим установившийся поток в подъемных трубах. По мере подъема жидкости температура ее понижается в результате теплообмена с окружающей средой. Получим уравнение теплового баланса.
Пусть в сечении h температура потока равна T(h), соответственно в сечении h + Δh – T (h + Δh). Время, за которое жидкость проходит расстояние Δh, равно 
, где u – скорость движения потока. Обозначим через с – теплоемкость системы, то изменение количества тепла в элементе (h; h + Δh) за время Δt будет равно:
где F – площадь поперечного сечения трубы.
Это же количество тепла передается окружающей среде. Предположим, что теплопередача происходит по закону Ньютона, получим:
ΔW = 2 · π · R · φ · (T - Tпор)
где R – радиус скважины; φ – теплопроводность; Tпор – температура горной породы.
Из последних двух соотношений при Δh → 0 находим
,
где а = 2 · π · R · φ / (F· C· U). Температура породы изменяется в зависимости от h (h = 0 соответствует забою скважины) по следующему закону
Tпор = T0 – k · h
k – геотемпературный градиент;
T0 – температура на забое скважины.
Теперь, зная зависимость вязкости от температуры μ = μ(Т) для нефти, можно определить изменение вязкости системы по глубине.
Здесь мы привели простейшую схему расчета, в которой не учтены зависимости растворенности газа в нефти и его объема от температуры, влияние нагрева окружающих пород и т.п. На основе рассмотренной схемы можно сделать следующие выводы:
1) при увеличении скорости потока потери давления на трение возрастают; однако при этом вязкость нефти в скважине снижается;
2) при определенных условиях снижение вязкости нефти с увеличением скорости движения может оказывать большое влияние на изменение гидравлического сопротивления;
3) зависимость потерь давления на трение от скорости движения имеет немонотонный характер, что имеет важное значение при установлении рабочих режимов насосных установок.
Выше были рассмотрены случаи движения ГЖС при установившихся режимах. Теперь рассмотрим модель работы скважины при неустановившемся режиме. Уравнение нестационарного притока жидкости имеет вид:
(1)
где Т – время переходного процесса в пласте; К – коэффициент продуктивности.
Рассмотрим графические зависимости совместной работы пласта и скважин.
Характеристика подъемника будет
Рс = f (Q) (2)
Обозначим координаты точки пересечения через (Рс1; Q1). Это означает, что одновременно выполняются условия:
Рс1 = f(Q1),
.
Исследуем устойчивость данного режима, для этого предположим, что забойное давление и дебит получили малые приращения:
P = Pc1 + δP,
Q = Q1 + δQ,
| δP | << Pc1,
| δQ | << Q1
Если δP и δQ возрастают во времени, то данный режим неустойчив. Представим выражения для P и Q в уравнение (1), то получим:
(3)
Рс1 + δP = f (Q1 + δQ) ≈ f (Q1) + f ′(Q1) · δQ (4)
Вычитая почленно из (3) и (4) соответственно (1) и (2), находим
δP = f ′(Q1) · δQ
Исключая из полученных соотношений δP, получаем уравнение относительно δQ:
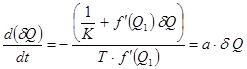(5)
Последнее уравнение (5) – линейное дифференциальное уравнение первого порядка. При а > 0 решение экспоненциально возрастает во времени (неустойчивый режим), при а < 0 – режим устойчив.
Таким образом, если рабочая точка находится на правой, возрастающей ветви зависимости f (Q), то f ′(Q1) >0 и а < 0. Возрастающий участок характеристики подъемника соответствует устойчивому режиму работы, а внизпадающий участок – неустойчивому.
Лекция №6
Эксплуатация фонтанных скважин
Фонтанирование скважин обычно происходит на вновь открытых месторождениях нефти, когда запас пластовой энергии велик, т.е. давление на забое скважин достаточно большое, чтобы преодолеть гидростатическое давление столба жидкости в скважине, противодавление на устье скважины и давление, расходуемое на преодоление трения, связанное с движением этой жидкости. Общим условием для работы любой фонтанирующей скважины будет следующее основное равенство:
Рз = Рг + Ртр + Ру
где Рз – давление на забое скважины; Рг – гидростатическое давление столба жидкости в скважине; Ртр – потери давления на трение в НКТ; Ру – давление на устье скважины.
Различают 2 вида фонтанирования скважин:
- артезианское фонтанирование, когда поднимается жидкость, не содержащая пузырьков газа;
- фонтанирование жидкости, содержащей пузырьки газа – наиболее распространенный способ фонтанирования.
Артезианское фонтанирование встречается при добыче нефти редко. Оно возможно в 2-х случаях:
1) полное отсутствие газа и Рз >> Рг;
2) при наличии растворенного газа в нефти, который не выделяется, т.к. Ру > Рнас и Рз > Рг + Ру;
Поскольку присутствие пузырьков газа в жидкости уменьшает плотность, то давление на забое скважины, необходимое для фонтанирования газированной жидкости существенно меньше, чем при артезианском фонтанировании.
Артезианское фонтанирование
Давление на забое скважины определяется по ф-ле (1), в которой
Рг = 
(2)
где 
- средняя плотность жидкости в скважине; Н – расстояние между забоем и устьем.
Для наклонных скважин:
H = L · cosα (3)
где L – расстояние от забоя до устья вдоль оси наклонной скважины; α – средний угол кривизны скважины.
При движении жидкости по НКТ она охлаждается и ее плотность меняется.
(4)
где ρз, ρу – плотность жидкости на устье и на забое скважины соответственно.
При фонтанировании обводненной нефти плотность жидкости подсчитывается:
ρз = ρн пл (1-n) + ρв пл · n (5)
ρу = ρн д (1-n) + ρв · n (6)
Ру определяется удаленностью скважины от групповой замерной установки или размером штуцера, устанавливаемого на выкидной линии фонтанирующей скважины для регулирования ее дебита.
Ртр определяется по следующей формуле:
(7)
где L – длина колонны НКТ; υж – скорость жидкости.
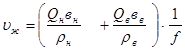(8)
где Qн, Qв – дебит нефти и воды, приведенный к стандартным условиям; ρн, ρв – плотность н и в в стандартных условиях; вн, вв – объемные коэффициенты; f – площадь сечения НКТ.
Диаметр НКТ существенно влияет на Ртр, например при уменьшении Ø на 10% (покрытие эпоксидными смолами) Ртр возрастают в 1,6 раза.
Коэффициент сопротивления λ определяется через число Re по соответствующим формулам.
Λ зависит от режима течения, при Re < 1200 течение ламинарное, при Re > 2500 – турбулентное и при 1200 < Re < 2500 – переходная зона:
При ламинарном течении
(9)
При турбулентном
(10)
Для переходной зоны
(11)
Приток жидкости из пласта в скважину
(12)
Решая относительно Рз, получим
(13)
При совместной работе пласта и фонтанного подъемника на забое скважины устанавливается Рз, определяющее такой приток жидкости, который фонтанные трубы будут в состоянии пропустить при данной глубине скважины, Ру, Ø НКТ и т.д. Для определения этого притока приравняем правые части уравнений (1) и (13):
(14)
Левая часть равенства зависит от Q, т.к. Ртр и Ру зависят от Q, с увеличением расхода Ртр и Ру – увеличиваются. Рг не зависит от Q. Заменим Ртр и Ру на некоторую функцию f(Q), тогда получим:
(15)
Из этого равенства надо найти Q. Для этого задаваясь различными Q вычисляем левую часть равенства:
А = Рг + f(Q) (16)
И правую часть
(17)
Далее строятся два графика А(Q) и В(Q), с увеличением QА возрастает, а В уменьшается.
Точка пересечения линий А и В определит условие совместной работы пласта и фонтанного подъемника, т.е. дает дебит скважины Qc и соответствующее этому дебиту Рз.
Фонтанирование за счет энергии газа
При фонтанировании за счет энергии газа плотность столба ГЖС в фонтанных трубах мала, поэтому гидростатическое давление такой смеси будет меньше. Следовательно, и для фонтанирования скважины потребуется меньше забойное давление.
В зоне, где Р < Рнас, из нефти выделяется газ, причем этого газа становится больше, чем меньше давление, т.е. чем больше разница давлений ΔР = Рнас – Р. В данном случае фонтанирование будет происходить при давлении на забое скважины, превышающем давление насыщения (Рз > Рнас), и газ будет выделяться на некоторой высоте в НКТ.
Возможен другой случай, когда фонтанирование происходит при Рз > Рнас.
Очевидно, Рз в любом случае будет
Рз = Рб + Р (18)
где Рб – давление у башмака НКТ при фонтанировании скважины с постоянным дебитом.
Р = (H - L) · g· ρ
гидростатическое давление столба жидкости между башмаком и забоем (H - L)
Н – глубина скважины;
L – длина НКТ;
ρ – средняя плотность жидкости.
С другой стороны Рз может быть определено через уровень жидкости в межтрубном пространстве
Рз = Р1 + Р2 (19)
где Р1 = h · ρ · g – гидростатическое давление в межтрубном пространстве; Р2 = Рм + ΔР – давление газа, находящегося в межтрубном пространстве, на уровне жидкости; Рм – давление газа, находящегося в межтрубном пространстве на устье скважины; ΔР – гидростатическое давление столба газа от уровня до устья.
ΔР = (H - h) · ρг · g,
где ρг – средняя плотность газа в затрубном пространстве.
Рз = h · g · ρ + Рм + (H - h) · ρг · g, (20)
Таким образом, в скважине фонтанирующей с постоянным дебитом, давление Рз должно быть const. Поэтому необходимо, чтобы уменьшение h сопровождалось увеличением давления Рм и наоборот.
Рассмотрим 2 случая фонтанирования:
1) Рз < Рнас
В этом случае свободный газ имеется на самом забое скважины. Часть газа поступает в межтрубное пространство и накапливается там. Накопление газа в затрубном пространстве приводит к увеличению давления Рм и соответствующему понижению уровня жидкости h на такую величину, чтобы Рз согласно уравнения (20) оставалось бы const. Этот процесс продолжается до тех пор, пока уровень не опустится до башмака труб. В этом случае можно достаточно точно определить
Рб = Рм + (H - h) · ρг · g (21)
где 
- плотность газа.
Рз >Рб и определяется по формуле (18).
Таким образом, при Рз < Рнас уровень жидкости в затрубном пространстве обязательно должен устанавливаться на уровне башмака НКТ после выхода работы скважины на установившейся режим. Это справедливо, если нет утечки газа через затрубное пространство.
2) Рз > Рнас
В этом случае свободный газ не накапливается в затрубном пространстве. В самих трубах газ начинает выделяться на некоторой высоте, где Р = Рнас. Различным положениям уровня будет соответствовать различные Рм. Т.к. h меняется, то становится невозможным определение Рз по величине Рм.
Условие фонтанирования
Фонтанирование возможно в случае, если энергия, приносимая на забой жидкостью, равна или > энергии, необходимой для подъема этой жидкости на поверхность при условии, что подъемник работает на режиме наибольшего к.п.д. Полезная работа при подъеме 1м3 жидкости равна произведению веса жидкости на высоту подъема:
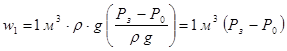[Дж] (22)
Вместе с нефтью на забой может поступать свободный газ, также при снижении давления происходит выделение газа из нефти. Общее кол-во газа, приходящееся на 1 м3 нефти, называется полным газовым фактором Г0. Газ, расширяясь, тоже совершает работу. Но эту работу совершает только свободный газ. Поэтому при подсчете работы расширения газа учитывается эффективный газовый фактор Гэф = Г0 – Граств.
По А.П.Крылову работа газа при изометрическом расширении
[Дж] (23)
Тогда общее количество энергии
(24)
Т.к. на устье скважины всегда есть некоторое противодавление Ру, то кол-во энергии, уносимое с жидкостью по аналогии:
(25)
Кол-во энергии, поступающей из пласта и затраченной на подъем жидкости
29-04-2015, 00:43