Для уменьшения времени распространения сигнала переноса применяют: конструктивные решения, когда используют в цепи переноса наиболее быстродействующие элементы; тщательно выполняют монтаж без длинных проводников и паразитных емкостных составляющих нагрузки и (наиболее часто) структурные методы ускорения прохождения сигнала переноса.
По способу организации межразрядных переносов параллельные сумматоры, реализующие структурные методы, делят на сумматоры:
· с последовательным переносом;
· с параллельным переносом;
· с групповой структурой;
· со специальной организацией цепей переноса.
По способу выполнения операции сложения и возможности сохранения результата сложения можно выделить три основных вида сумматоров:
· комбинационный, выполняющий микрооперацию "S = A плюс B", в котором результат выдается по мере его образования (это комбинационная схема в общепринятом смысле слова);
· сумматор с сохранением результата "S = A плюс B";
· накапливающий, выполняющий микрооперацию "S = S плюс B".
Последние две структуры строятся либо на счетных триггерах (сейчас практически не используются), либо по структуре "комбинационный сумматор регистр хранения" (сейчас наиболее употребляемая схема).
Важнейшими параметрами сумматоров являются:
· разрядность;
· статические параметры: Uвх, Uвх, Iвх и так далее, то есть обычные параметры интегральных схем;
· динамические параметры. Сумматоры характеризуются четырьмя задержками распространения;
· от подачи входного переноса до установления всех выходов суммы при постоянном уровне на всех входах слагаемых;
· от одновременной подачи всех слагаемых до установления всех выходов суммы при постоянном уровне на входе переноса;
· от подачи входного переноса до установления выходного переноса при постоянном уровне на входах слагаемых;
· от подачи всех слагаемых до установления выходного переноса при постоянном уровне на входах слагаемых.
4. Счётчики
Счётчик числа импульсов – устройство, на выходах которого получается двоичный (двоично-десятичный) код, определяемый числом поступивших импульсов. Счётчики могут строиться на T-триггерах. Основной параметр счётчика – модуль счёта – максимальное число единичных сигналов, которое может быть сосчитано счётчиком. Счётчики обозначают через СТ (от англ. counter).
Счётчики классифицируют:
1) по числу устойчивых состояний триггеров:
· на двоичных триггерах;
· на троичных триггерах;
· на n-ичных триггерах.
2) по модулю счёта:
· двоично-десятичные (декада);
· двоичные;
· с произвольным постоянным модулем счёта;
· с переменным модулем счёта.
3) по направлению счёта:
· суммирующие;
· вычитающие;
· реверсивные.
4) по способу формирования внутренних связей:
· с последовательным переносом;
· с параллельным переносом;
· с комбинированным переносом;
· кольцевые.
5) по способу переключения триггера:
· синхронные;
· асинхронные.
Схему двоичного счетчика можно получить с помощью формального синтеза, однако более наглядным путем представляется эвристический. Таблица истинности двоичного счетчика — последовательность двоичных чисел от нуля до 2n − 1, где n - разрядность счётчика. Наблюдение за разрядами чисел, составляющих таблицу, приводит к пониманию структурной схемы двоичного счетчика. Состояния младшего разряда при его просмотре по соответствующему столбцу таблицы показывают чередование нулей и единиц вида 01010101..., что естественно, т. к. младший разряд принимает входной сигнал и переключается от каждого входного воздействия. В следующем разряде наблюдается последовательность пар нулей и единиц вида 00110011... . В третьем разряде образуется последовательность из четверок нулей и единиц 00001111... и т.д. Из этого наблюдения видно, что следующий по старшинству разряд переключается с частотой, в два раза меньшей, чем данный. Известно, что счетный триггер делит частоту входных импульсов на два. , Сопоставив этот факт с указанной выше закономерностью, видим, что счетчик может быть, построен в виде цепочки последовательно включенных счетных триггеров. Заметим, кстати, что согласно ГОСТу входы элементов изображаются слева, а выходы справа. Соблюдение этого правила ведет к тому, что в числе, содержащемся в счетчике, младшие разряды расположены левее старших.
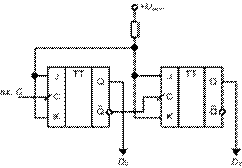
Рис. 9. Двухразрядный двоичный счётчик с последовательной организацией переноса на T-триггере.
5. Регистры
Регистр – последовательное логическое устройство, используемое для хранения n-разрядных двоичных слов (чисел) и выполнения преобразований над ними.
Регистр представляет собой упорядоченную последовательность триггеров, число которых соответствует числу разрядов в слове. С каждым регистром обычно связано комбинационное цифровое устройство, с помощью которого обеспечивается выполнение некоторых операций над словами.
Фактически любое цифровое устройство можно представить в виде совокупности регистров, соединённых друг с другом при помощи комбинационных цифровых устройств.
Основой построения регистров являются D-триггеры, RS-триггеры.
Регистры классифицируются по следующим видам:
· накопительные (регистры памяти, хранения);
· сдвигающие.
В свою очередь сдвигающие регистры делятся:
1) по способу ввода-вывода информации:
· параллельные – запись и считывание информации происходит одновременно на все входы и со всех выходов;
· последовательные – запись и считывание информации происходит в первый триггер, а та информация, которая была в этом триггере, перезаписывается в следующий - то же самое происходит и с остальными триггерами;
· комбинированные.
2) по направлению передачи информации:
· однонаправленные;
· реверсивные.
Регистром называется функциональный узел, осуществляющий приём, хранение и передачу информации. Регистры состоят из группы триггеров, обычно D. По типу приёма и выдачи информации различают 3 типа регистров:
· С последовательным приёмом и выдачей информации — сдвиговые регистры;
· С параллельным приёмом и выдачей информации — параллельные регистры;
· С параллельно-последовательным приёмом и выдачей информации.
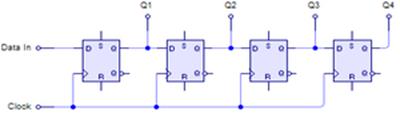
Рис. 10. 4-х разрядный сдвиговый регистр, преобразователь последовательного кода в параллельный и обратно
6.Шифратор
Шифратор (кодер) преобразует единичный сигнал на одном из входов в n-разрядный двоичный код. Наибольшее применение он находит в устройствах ввода информации (пультах управления) для преобразования десятичных чисел в двоичную систему счисления. Предположим, на пульте десять клавиш с гравировкой от 0 до 9. При нажатии любой из них на вход шифратора подается единичный сигнал (
). На выходе шифратора должен появиться двоичный код (
)этого десятичного числа. Как видно из таблицы истинности (табл. 2), в этом случае нужен преобразователь с десятью входами и четырьмя выходами.
| Входы |
Выходы |
|||
| X |
Y3 |
Y2 |
Y1 |
Y0 |
| 0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
1 |
| 2 |
0 |
0 |
1 |
0 |
| 3 |
0 |
0 |
1 |
1 |
| 4 |
0 |
1 |
0 |
0 |
| 5 |
0 |
1 |
0 |
1 |
| 6 |
0 |
1 |
1 |
0 |
| 7 |
0 |
1 |
1 |
1 |
| 8 |
1 |
0 |
0 |
0 |
| 9 |
1 |
0 |
0 |
1 |
Табл. 2. Таблица истинности
7. Дешифратор
Дешифратор (декодер) – комбинационное устройство, преобразующее n-разрядный двоичный, троичный или k-ичный код в 
-ичный одноединичный код, где k - основание системы счисления. Логический сигнал появляется на том выходе, порядковый номер которого соответствует двоичному, троичному или k-ичному коду.
Дешифраторы являются устройствами, выполняющими двоичные, троичные или k-ичные логические функции (операции).
Часто дешифраторы дополняются входом разрешения работы E. Если на этот вход поступает единица, то дешифратор функционирует, в ином случае на выходе дешифратора вырабатывается логический ноль вне зависимости от входных сигналов.
Существуют дешифраторы с инверсными выходами, у такого дешифратора выбранный разряд показан нулём.
Функционирование дешифратора описывается системой конъюнкций:
…………………………………………………………
Обратное преобразование осуществляет шифратор.
Дешифраторы - это комбинационные схемы с несколькими входами и выходами, преобразующие код, подаваемый на входы в сигнал на одном из выходов. На выходе дешифратора появляется логическая единица, на остальных — логические нули, когда на входных шинах устанавливается двоичный код определённого числа или символа, то есть дешифратор расшифровывает число в двоичном, троичном или k-ичном коде, представляя его логической единицей на определённом выходе. Число входов дешифратора равно количеству разрядов поступающих двоичных, троичных или k-ичных чисел. Число выходов равно полному количеству различных двоичных, троичных или k-ичных чисел этой разрядности.
Для n-разрядов на входе, на выходе 2n, 3n или kn. Чтобы вычислить, является ли поступившее на вход двоичное, троичное или k-ичное число известным ожидаемым, инвертируются пути в определённых разрядах этого числа. Затем выполняется конъюнкция всех разрядов преобразованного таким образом числа. Если результатом конъюнкции является логическая единица, значит на вход поступило известное ожидаемое число.
Из логических элементов являющихся дешифраторами можно строить дешифраторы на большое число входов. Каскадное подключение таких схем позволит наращивать число дифференцируемых переменных.
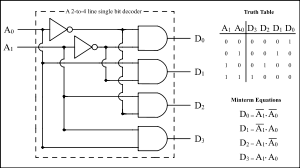
Рис. 11. Пример дешифратора 2×4
Заключение
В ходе данной работы были достигнуты поставленные цели рассмотрения логических устройств применяемых в ЭВМ, как они устроены и функционируют.
Триггеры подразделяются на две большие группы — динамические и статические. Названы они так по способу представления выходной информации. Статические (потенциальные) триггеры, в свою очередь, подразделяются на две неравные по практическому значению группы — симметричные и несимметричные триггеры. Оба класса реализуются на двухкаскадном усилителе с положительной обратной связью, а названием своим они обязаны способам организации внутренних электрических связей между элементами схемы. Статистические триггеры могут классифицироваться двумя способами: функциональный и по вводу информации.
Полусумматор — логическая схема имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров.
Сумматор – логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. Сумматоры классифицируют по системе счисления, одновременно обрабатываемых разрядов складываемых чисел, числу входов и выходов одноразрядных двоичных сумматоров, способу представления и обработки складываемых чисел.
Счётчик числа импульсов – устройство, на выходах которого получается двоичный (двоично-десятичный) код, определяемый числом поступивших импульсов. Счётчики классифицируются по числу устойчивых состояний триггеров, модулю счёта, направлению счёта, способу формирования внутренних связей, способу переключения триггера.
Регистр – последовательное логическое устройство, используемое для хранения n-разрядных двоичных слов (чисел) и выполнения преобразований над ними. Регистры классифицируются на накопительные и сдвигающие. Вторые же – по способу ввода-вывода информации и направлению передачи информации.
Шифратор (кодер) преобразует единичный сигнал на одном из входов в n-разрядный двоичный код. Наибольшее применение он находит в устройствах ввода информации (пультах управления) для преобразования десятичных чисел в двоичную систему счисления.
Дешифратор (декодер) – комбинационное устройство, преобразующее n-разрядный двоичный, троичный или k-ичный код в 
-ичный одноединичный код, где k - основание системы счисления. Из логических элементов являющихся дешифраторами можно строить дешифраторы на большое число входов. Каскадное подключение таких схем позволит наращивать число дифференцируемых переменных.
Список используемой литературы
1. Зельдин Е.А. Цифровые интегральные микросхемы в информационно-измерительной аппаратуре. – Л.: Энергоатомиздат. Ленингр. отд-ние, 1986. – 280 с.
2. Каган Б.Н. Электронные вычислительные машины и системы: Учеб. пособие для вузов. – 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1985. – 552 с.
3. Шило В.А. Популярные цифровые микросхемы: Справочник. – Челябинск: Металлургия, Челябинское отделение, 1988. – 352 с.
4. Микропроцессоры и микропроцессорные комплекты интегральных микросхем: Справочник: В 2 Т. / Н.Н. Аверьянов, А.И. Березенко, Ю.И. Борщенко и др.; Под редакцией В.А. Шехнова. – М.: Радио и связь, 1988. – Т.2. – 368 с.
5. Соломатин Н.М. Логические элементы ЭВМ. М.: Высш. шк., 2000. - 160 с.
6. Букреев И.Н., Горячев В.И., Мансуров Б.М. Микроэлектронные схемы цифровых устройств. М.: Радио и связь, 2000. - 416 с.
29-04-2015, 05:18