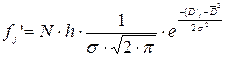78,2
Решение:
1. Данные об объеме израсходованного в единицу времени материала систематизируются в возрастающем порядке от D1 до DN, где Di
-1
<=Di
<=Di
+1
. Затем весь интервал имеющихся значений разбивается на Ь равных интервалов длиной h, каждый из которых содержит несколько значений Di
. После этого находятся середины интервалов по формуле:
, где 
- соответственно начало и конец 
того интервала. Каждому 
соответствует значение частоты 
, определяемое как количество 
, попавших в тый интервал, 
.
Минимальное значение 
.
Значение первой недели, равное 0, когда производственный процесс еще не начался, не рассматриваем, т.к. это нетипичное значение расхода материала. Также не рассматриваем значения недель №№18 и 19, на которые выпадают праздники.
Максимальное значение 
.
Тогда 
Группировка данных на 10 равноинтервальных групп будет иметь вид:
| № интервала |
Границы интервала |
Середина интервала, |
Частота, |
| 1 |
63,40 – 72,14 |
67,770 |
4 |
| 2 |
72,14 – 80,88 |
76,511 |
3 |
| 3 |
80,88 – 89,62 |
85,251 |
6 |
| 4 |
89,62 – 98,36 |
93,991 |
7 |
| 5 |
98,36 – 107,10 |
102,731 |
7 |
| 6 |
107,10 – 115,84 |
111,471 |
5 |
| 7 |
115,84 – 124,58 |
120,211 |
4 |
| 8 |
124,58 – 133,32 |
128,951 |
8 |
| 9 |
133,32 -142,06 |
137,691 |
3 |
| 10 |
142,06 – 150,80 |
146,431 |
2 |
| Итого |
49 |
2. 
Далее производится оценка математического ожидания, дисперсии и среднеквадратического отклонения распределения вероятностей интенсивности расходования материалов. Эти параметры оцениваются при помощи следующих формул:
| № интервала |
Границы интервала |
Середина интервала, |
Частота, |
|
|
| 1 |
63,40 – 72,14 |
67,770 |
4 |
271,08 |
5665,86 |
| 2 |
72,14 – 80,88 |
76,511 |
3 |
229,53 |
2504,84 |
| 3 |
80,88 – 89,62 |
85,251 |
6 |
511,50 |
2437,46 |
| 4 |
89,62 – 98,36 |
93,991 |
7 |
657,93 |
912,19 |
| 5 |
98,36 – 107,10 |
102,731 |
7 |
719,11 |
50,11 |
| 6 |
107,10 – 115,84 |
111,471 |
5 |
557,35 |
183,89 |
| 7 |
115,84 – 124,58 |
120,211 |
4 |
480,84 |
876,70 |
| 8 |
124,58 – 133,32 |
128,951 |
8 |
1031,60 |
4434,76 |
| 9 |
133,32 -142,06 |
137,691 |
3 |
413,07 |
3126,87 |
| 10 |
142,06 – 150,80 |
146,431 |
2 |
292,86 |
3366,02 |
| Итого |
49 |
5164,89 |
23558,71 |
||
| Математическое ожидание
|
105,4 |
||||
| Дисперсия =итого/49 |
480,8 |
||||
| Ср.квадр.откл.= корень (Дисп) |
21,90 |
||||
=итого/493. Затем делается предположение о характере распределения вероятностей. В частности, если 
для всех значений 
, то можно предположить, что интенсивность расходования материала является нормально распределенной непрерывной величиной. В случае, если 
, то можно сделать предположение о показательном распределении интенсивности расходования материалов. В случае, если каждое значение встречается с одинаковой частотой, предполагается равномерное распределение вероятностей.
| № интервала |
Границы интервала |
|
|
| 1 |
63,40 – 72,14 |
37,64 |
65,781 |
| 2 |
72,14 – 80,88 |
28,90 |
65,781 |
| 3 |
80,88 – 89,62 |
20,16 |
65,781 |
| 4 |
89,62 – 98,36 |
11,42 |
65,781 |
| 5 |
98,36 – 107,10 |
2,68 |
65,781 |
| 6 |
107,10 – 115,84 |
6,06 |
65,781 |
| 7 |
115,84 – 124,58 |
14,80 |
65,781 |
| 8 |
124,58 – 133,32 |
23,54 |
65,781 |
| 9 |
133,32 -142,06 |
32,28 |
65,781 |
| 10 |
142,06 – 150,80 |
41,02 |
65,781 |
= 105,4
Практически для всех интервалов получили, что выполняется неравенство 
. Поэтому я считаю, что распределение вероятностей подчиняется нормальному закону.
Для проверки правильности сделанного предположения рассчитываются выравнивающие частоты значений по формуле: 
.
В частности, если предполагается:
- нормальное распределение вероятностей интенсивности расходования материалов, то выравнивающие частоты рассчитываются по формуле:
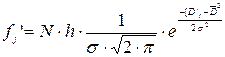
- показательное распределение вероятностей интенсивности расходования материалов, то выравнивающие частоты рассчитываются по формуле:
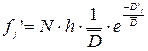
- равномерное распределение вероятностей интенсивности расходования материалов, то выравнивающие частоты рассчитываются по формуле:
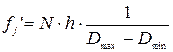
Произведя расчет для вычисления теоретических значений частот, получили, что они достаточно близки к данным наблюдений.
| № интервала |
Середина интервала |
Частота, |
|
|
|
| 1 |
67,770 |
4 |
0,229 |
0,018 |
1,79 |
| 2 |
76,511 |
3 |
0,420 |
0,018 |
3,27 |
| 3 |
85,251 |
6 |
0,655 |
0,018 |
5,11 |
| 4 |
93,991 |
7 |
0,873 |
0,018 |
6,80 |
| 5 |
102,731 |
7 |
0,993 |
0,018 |
7,73 |
| 6 |
111,471 |
5 |
0,962 |
0,018 |
7,50 |
| 7 |
120,211 |
4 |
01,796 |
0,018 |
6,20 |
| 8 |
128,951 |
8 |
0,562 |
0,018 |
4,38 |
| 9 |
137,691 |
3 |
0,338 |
0,018 |
2,64 |
| 10 |
146,431 |
2 |
0,174 |
0,018 |
1,35 |
4. Для проверки гипотезы о характере распределения используется критерий Пирсона.
Согласно критерию Пирсона, если случайная величина подчиняется предполагаемому распределению, то следующее неравенство выполняется с вероятностью, равной 
:
,
где 
- наблюдаемое значение 
- критическое значение . Пусть 
(уровень значимости), тогда вероятность = 1- 0,05 = 0,95.
,
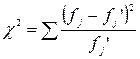, где 
- число параметров, которыми определяется предполагаемое распределение. 
, т.к. рассматриваем 2 параметра - 
(интенсивность поступления товара на предприятие) и 
(частоту появления того или иного значения признака).
В данном случае - 
.
| № интервала |
Границы интервала |
Середина интервала, |
Частота, |
|
|
| 1 |
63,40 – 72,14 |
67,770 |
4 |
1,79 |
2,744 |
| 2 |
72,14 – 80,88 |
76,511 |
3 |
3,27 |
0,022 |
| 3 |
80,88 – 89,62 |
85,251 |
6 |
5,11 |
0,156 |
| 4 |
89,62 – 98,36 |
93,991 |
7 |
6,80 |
0,006 |
| 5 |
98,36 – 107,10 |
102,731 |
7 |
7,73 |
0,070 |
| 6 |
107,10 – 115,84 |
111,471 |
5 |
7,50 |
0,833 |
| 7 |
115,84 – 124,58 |
120,211 |
4 |
6,20 |
0,783 |
| 8 |
124,58 – 133,32 |
128,951 |
8 |
4,38 |
2,997 |
| 9 |
133,32 -142,06 |
137,691 |
3 |
2,64 |
0,050 |
| 10 |
142,06 – 150,80 |
146,431 |
2 |
1,35 |
0,309 |
| Итого |
49 |
7,969 |
Полученное значение критерия Пирсона говорит о том, что гипотеза о выборе нормального закона распределения признака подтверждается.
5. Оптимальный уровень текущего запаса в момент поставки пополнения определяется по формуле: 
,
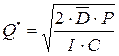где 
- расходы на доставку, 
- коэффициент издержек содержания, 
- цена запасаемого материала.
(кг)
Оптимальная периодичность поставок (длительность цикла) рассчитывается по формуле: 
недели.
Всего будет 52 / 2 = 26 поставок материалов.
Затем определяется величина коэффициента 
: 
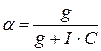, где 
- издержки, связанные с дефицитом запасаемого материала.
Определяется размер страхового запаса при помощи уравнения:
где 
- размер страхового запаса;
- функция плотности распределения вероятностей значения спроса на запасаемый материал.
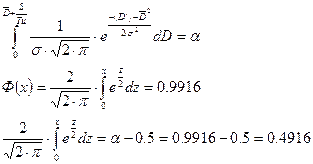
Тогда страховой запас будет равен около 27 кг.
Первая поставка = 200 + 27 =227 кг
Остальные поставки – по 200 кг.
Общий расход материалов равен 5216,86.
Проверим какими будут остатки материалов на складе в течении года, возможно, нужно будет подкорректировать размеры некоторых партий поставки.
6. Нарисовать схему процесса пополнения и расходования запаса товара.
Таблица.
Величина остатков товара на складе.
| № недели |
Исходный вариант графика поставок |
Скорректированный график поставок |
||||||
| Размер поставки |
Запас на начало недели |
Расход за неделю |
Остаток на конец недели |
Размер поставки |
Запас на начало недели |
Расход за неделю |
Остаток на конец недели |
|
| 1 |
227 |
0 |
0 |
227,0 |
||||