Приведенные соображения с достаточной наглядностью демонстрируют прогрессивность внедрения в практику цифровой рентгенографии, которая сможет перевести диагностическую рентгенологию на новый более высокий технологический уровень. Отказ от дорогостоящих расходных материалов обнаруживает и ее высокую экономическую эффективность, что в сочетании с возможностью уменьшения лучевых нагрузок на пациентов делает ее применение в практике особенно привлекательным. [№ 6]
3.3. Цифровая рентгенография с экрана электронно-оптического преобразователя (ЭОП).
Система рентгенографии с экрана ЭОП (рис. 5) состоит, как и обычная система электронно-оптического преобразования для просвечивания, из ЭОП, телевизионного тракта с высоким разрешением, рентгеновского высоковольтного генератора и рентгеновского излучателя. Сюда же входит штатив для исследования, цифровой преобразователь изображения и другие компоненты.
При обычной методике рентгенографии с экрана ЭОП с помощью 100 мм фотокамеры или кинокамеры переснимается оптическое изображение на выходном экране преобразователя.
В цифровой же системе сигнал, поступающий с видеокамеры, аналого-цифровым преобразователем трансформируется в набор цифровых данных и передается в накопительное устройство. Затем эти данные, в соответствии с выбранными исследователем параметрами, компьютерное устройство переводит в видимое изображение.
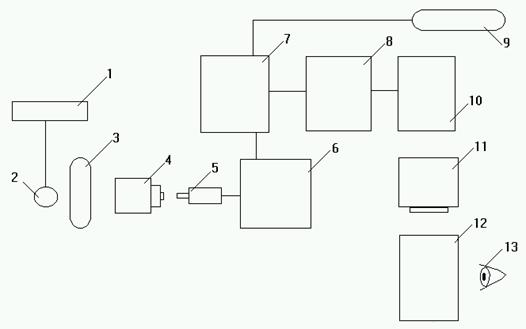Рис.5 Цифровая рентгенография с экрана ЭОП
1-генератор; 2-рентгеновская трубка; 3-пациент; 4-ЭОП; 5-видеокамера;
6-аналого-цифровой преобразователь; 7-накопитель изображений;
8-видеопроцессор; 9-сеть; 10-цифро-аналоговый преобразователь;
11-монитор; 12-снимок; 13-рентгенолог.
3.4.Цифровая люминесцентная рентгенография (ЦЛР).
Применяемые в ЦЛР (рис.6) пластины-приемники изображения после их экспонирования рентгеновским излучением последовательно, точка за точкой, сканируются специальным лазерным устройством, а возникающий в процессе лазерного сканирования световой пучок трансформируется в цифровой сигнал. После цифрового усиления контуров и контрастности элементов изображения оно лазерным принтером печатается на пленке или воспроизводится на телевизионном мониторе рабочей консоли. Люминесцентные пластины-накопители выпускаются в стандартных формах рентгеновской пленки, помещаются вместо обычных комплектов «пленка-усиливающий экран» в кассету и применяются в обычных рентгеновских аппаратах.
Такая пластина обладает значительно большей экспозиционной широтой, чем общепринятые комбинации пленка-экран, благодаря чему значительно расширяется интервал между недо- и переэкспонированием. Этим способом можно получать достаточно контрастные изображения даже при резко сниженной экспозиционной дозе, нижним пределом которой является лишь уровень квантового шума. Поэтому даже при рентгенографии в палате у постели больного методика ЦЛР гарантирует получения качественного снимка.
При ЦЛР используются цифровые преобразователи, пространственное разрешение которых выше, чем у большинства используемых в настоящее время для обычной рентгенографии комбинаций экран-пленка. Все же особым преимуществом ЦЛР является передача малоконтрастных деталей, тогда как передача очень мелких деталей, таких, например, как микрокальценаты в молочной железе, остается прерогативой рентгенографии на рентгеновской пленке.
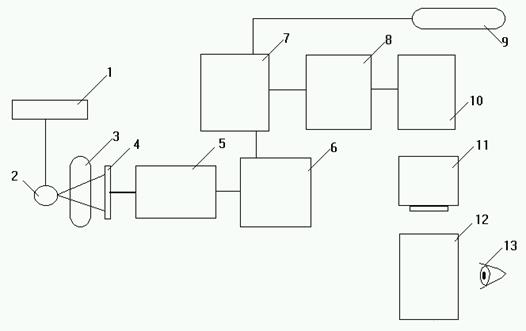Рис. 6 Цифровая люминесцентная рентгенография.
1-генератор; 2-рентгеновская трубка; 3-пациент; 4-запоминающая
пластина; 5-транспортирующее устройство; 6-аналого-цифровой
преобразователь; 7-накопитель изображений;8-видеопроцессор; 9-сеть;
10-цифро-аналоговый преобразователь; 11-монитор; 12-снимок;
13-рентгенолог.
3.5. Селеновая рентгенография.
Селеновые детекторы представляют собой новейшую систему цифровой рентгенографии (рис. 7). Основной частью такого устройства служит детектор в виде барабана, покрытого слоем аморфного селена. Селеновая рентгенография в настоящее время используется только в системах рентгенографии грудной клетки. Характерная для снимков грудной клетки высокая контрастность между легочными полями и областью средостения при цифровой обработке сглаживается, не уменьшая при этом контрастности деталей изображения. Другим преимуществом селенового детектора является высокий коэффициент отношения сигнал/шум.
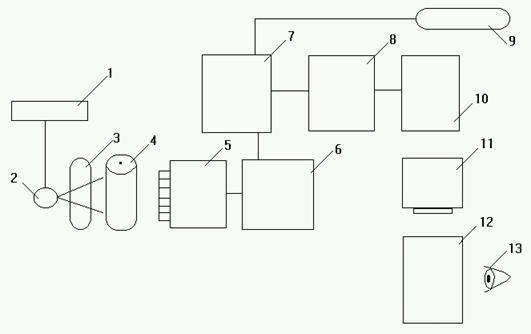
Рис.5 Цифровая селеновая рентгенография.
1-генератор; 2-рентгеновская трубка; 3-пациент; 4-селеновый барабан;
5-сканирующие электроды+усилитель; 6-аналого-цифровой преобразо-
ватель; 7-накопитель изображений; 8-видеопроцессор; 9-сеть;
10-цифро-аналоговый преобразователь; 11-монитор; 12-снимок;
13-рентгенолог.
4. Математические основы компьютерной томографии
Исследования внутренней структуры объектов с помощью рентгеновского излучения широко распространены и хорошо известны. Ослабление рентгеновского излучения вдоль луча, соединяющего источник и приемник, является интегральной характеристикой плотности исследуемого объекта. С математической точки зрения речь идет о задаче восстановления функции по ее интегральным значениям вдоль некоторого семейства лучей. Различные лучи соответствуют различным (относительно объекта) положениям источника и приемника излучения. Такая модель является простейшей, но во многих случаях хорошо отражает реальную ситуацию и подтверждается исследованиям реальных тестовых объектов. Плотность реальных объектов является функцией трех пространственных координат. Однако в классической компьютерной томографии трехмерный объект представляют в виде набора тонких срезов. Внутри каждого среза плотность считают функцией только двух переменных. При исследовании фиксированного среза систему источник-приемник устраивают таким образом, что регистрируются данные только по лучам, лежащим в тонком слое относительно центральной плоскости среза. Таким образом приходят к задаче восстановления функции двух переменных по ее интегральным значениям вдоль некоторого семейства лучей Для регистрации в веерной схеме, чаще встречающейся в реальных томографах, используется линейка детекторов, различные положения источника относительно объекта обеспечиваются вращением системы регистрации или объекта.
4.1. Математическая постановка задачи рентгеновской компьютерной томографии, преобразование Радона и формулы обращения.
В компьютерной рентгеновской томографии трехмерный объект представляется обычно в виде набора тонких срезов. Для восстановления плотности среза решается задача обращения двумерного преобразования Радона. Преобразованием Радона функции f(x, y) называется функция, 
определяемая равенством 
.
Обычно для восстановления функции двух переменных по ее интегралам вдоль прямых используется метод свертки и обратного проецирования. В этом методе формула обращения преобразования Радона записывается без явного использования обобщенных функций. Однако наиболее общий и естественный вид формулы обращения преобразования Радона приобретают при использовании аппарата обобщенных функций. Далее будет рассмотрено соотношение между методом обобщенных функций и методом свертки и обратного проецирования.
Перед изложением собственно численного алгоритма будет дан вывод формулы обращения, позволяющий естественным образом перейти к построению алгоритма.
В силу равенства
функция 
при любом фиксированном p
определяется своими значениями при 
. Это позволяет нам перейти к функции
.
Здесь L(r, φ) - прямая, ортогональная лучу, имеющему угол φ ρ положительным направлением оси X, и отстоящая от начала координат на расстояние r (r
0), при r < 0 L(r, φ) - прямая, симметричная относительно начала координат прямой L(|r|, φ). Выразим f(x, y) через I(r, φ).
Поскольку
,
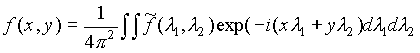где 
- преобразование Фурье функции f, то, переходя к полярным координатам после элементарных преобразований интеграла по φ на интервале [π, 2π], οолучаем
.
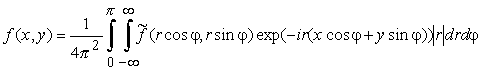Введем функцию S(z, φ), полагая
.
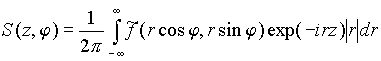При фиксированном φ функция S(z, φ) εсть обратное одномерное преобразование Фурье от произведения 
и |r|. Для справедливо равенство
.
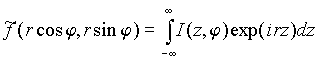Обратное преобразование Фурье от |r| есть обобщенная функция v1/πz2
. Переходя от преобразования Фурье произведения к свертке, получаем S(z,φ) = I(z,φ)
(v1/πz2
). Используя регуляризацию функции 1/z2
[19] приходим к выражению
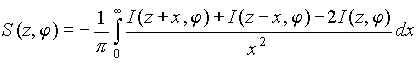. (1.5.1)
Таким образом, для f(x, y) справедлива формула
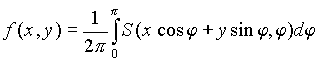, (1.5.2)
позволяющая выразить искомую функцию через наблюдаемые данные.
Прежде чем перейти к дискретному варианту сделаем ряд замечаний, связанных с обоснованием корректности рассматриваемых алгоритмов в реальных ситуациях. Обобщенные функции являются функционалами над пространством бесконечно дифференцируемых быстро убывающих функций. Однако при построении аппроксимаций исходных реальных данных по отсчетам, заданным в дискретных точках, желательно иметь менее жесткие требования к гладкости аппроксимирующих функций. Свертка с обобщенными функциями, в частности, с функцией 1/z2 , может быть определена для значительно менее гладких функций, это очень важно при доказательстве корректности применения численных алгоритмов, получаемых с помощью аппарата обобщенных функций, к реальным данным.
Перейдем к дискретному варианту. Будем предполагать, что f(x, y) = 0 вне круга радиуса R с центром в нуле. Исходными данными являются величины I(ri , φi ), здесь ri v отсчеты в интервале [-R, R], 1 ≤ i ≤ M - отсчеты в интервал [0, π], 1 ≤ j ≤ N. Если теперь при заданных значениях функции I(r, φ) β отсчетах (ri , φi ) построить аппроксимацию I(r, φ) так, что для S(z,φ) βыполняется равенство (1.5.1), то используя (1.5.1) и (1.5.2) можно получить приближение к f(x, y). В дальнейшем будем предполагать, что отсчеты на осях r и φ являются равноотстоящими.
При каждом фиксированном φj
определим 
следующим образом.
1. Функция имеет непрерывную первую производную по r.
2. В узлах решетки аппроксимирующая функция совпадает с заданными отсчетами, а ее производная в этих точках равна выборочной. То есть справедливы равенства: 
, 
, здесь h = 2R/(M-1), I(r0
,φj
) = I(rM+1
, φj
) = 0, i = 1, -, M.
3. На интервале [ri
, ri+1
] функция есть полином третьей степени от r.
Перечисленные условия позволяют в явном виде получить коэффициенты соответствующего сплайна. Непосредственными вычислениями можно получить, что
,
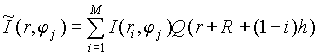где
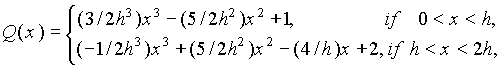
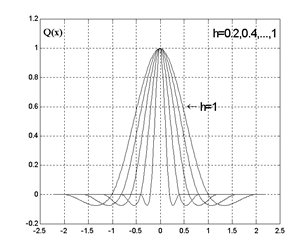
Q(x) = Q(-x), Q(x) = 0 при |x|> 2h, h=ri+1 -ri .
Функция Q(x) имеет разрывы второй производной, но модуль второй производной интегрируем, используя это обстоятельство можно показать, что свертка S0
(z) = Q(x) (-1/πz2
) выражается формулой (1.5.1). Непосредственными вычислениями получаем
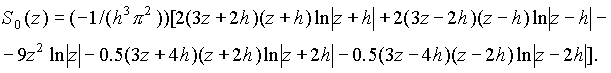
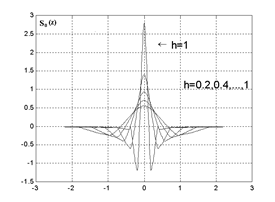
Графики функций Q(x) и S0 (z) для различных значений h представлены на рис. 1и рис. 2.
Таким образом,
.
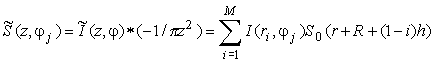Заменяя в (1.5.2) S на 
и интеграл частной суммой, получаем f*
(x, y) - приближение к функции f(x, y),
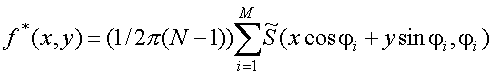. (1.5.3)
Как уже отмечалось выше, обычно в компьютерной томографии используется метод свертки и обратного проецирования. Рассмотрим соотношение между этим методом и методом, изложенным в настоящем параграфе. Используя интегрирование по частям, свертку с обобщенной функцией 1/z2 можно заменить дифференцированием и сверткой с 1/z (преобразованием Гильберта).
То есть функцию
S(z, φ) = I(z, φ) 1/z2
можно представить в виде
S(z, φ) = Iz
/
(z, φ) 1/z
При построении численных алгоритмов вместо обобщенной функции 1/z или, что то же самое, интеграла в смысле главного значения, в методе свертки и обратного проецирования используют некоторую последовательность регулярных функций pА (z), сходящуюся к 1/z (в смысле обобщенных функций) при A стремящемся к бесконечности. Используя интегрирование по частям, дифференцирование переносят на функции pА (z) и таким образом получают регулярные функции, сходящиеся к 1/z2 , то есть свертка с обобщенной функцией 1/z2 заменяется последовательностью сверток с регулярными функциями p/ А (z).
Таким образом, шаг свертки в классическом методе можно интерпретировать следующим образом: исходные данные аппроксимируются ступенчатой функцией и осуществляется свертка с регулярной функцией, являющейся приближением к обобщенной функцией 1/z2 .
В методе настоящего параграфа исходные данные аппроксимируются более гладкими функциями - сплайнами 3-го порядка. Это позволяет точно вычислить свертку с обобщенной функцией 1/z2 , причем в явном виде.
Шаг обратного проецирования соответствующий интегрированию свертки в обоих алгоритмах одинаков.
При использовании алгоритмов в реальных ситуациях важно уметь оценивать влияние шумов на точность получаемых приближений. Наличие явного выражения для аппроксимирующей функции позволяет вычислить дисперсию ошибки в любой точке при фиксированных δr, δφ θ известных статистических характеристиках шума. Для случая независимого, аддитивного, стационарного шума ξ (z) можно сделать следующее замечание. Рассмотрим процесс η, являющийся сверткой с 1/z2 процесса ξ. Спектральная плотность этого линейного преобразования есть |λ|. Для спектральных плотностей процессов ξ и η получаем соотношение f η (λ) = |λ|2 fξ (λ). Δисперсия процесса η конечна, если интегрируема fη (λ), ςо есть процесс ξ дифференцируем в среднеквадратическом. Для того, чтобы свертка выражалась формулой (1.5.1), на процесс ξ нужно наложить дополнительные условия, потребовав, например, чтобы выборочные функции с вероятностью единица имели конечную вторую производную.
Численное моделирование и восстановление плотности реальных объектов с использование метода, изложенного в настоящем параграфе, показало высокую точность метода, особенно при исследовании объектов и дефектов, имеющих сложную конфигурацию и участки с резкими границами.
Примеры восстановления, с использованием методов, изложенных в настоящем параграфе, приведены на рисунке 3. Тестовый объект состоит из 10 частиц. Рис.3(слева) соответствует 10 поворотам и Рис.3 (справа) соответствует 32 поворотам.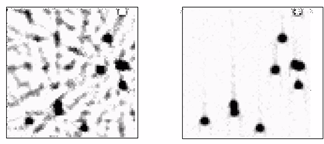 
4.2. Приведение формул обращения томографической реконструкции в конусе лучей к виду, позволяющему строить численные алгоритмы.
В компьютерной рентгеновской томографии трехмерный объект представляется обычно в виде набора тонких срезов. Для восстановления плотности среза решается задача обращения двумерного преобразования Радона. Для исследования ряда объектов более естественной является другая схема, когда источник излучения движется по некоторой пространственной кривой. Каждой точке кривой соответствует конус лучей, проходящих через эту точку. Исходными данными являются данные об ослаблении излучения при прохождении через объект. Математически задача ставится как задача восстановления функции трех переменных по интегралам вдоль прямых, проходящих через заданную кривую. Была получена формула обращения для функций, имеющих финитный носитель, и для кривых, удовлетворяющих определенным условиям. Главным в этих условиях является то, что любая плоскость, пересекающая объект пересекает кривую, по которой движется источник. Примером кривой, удовлетворяющей условиям, является совокупность двух единичных окружностей, лежащих во взаимно перпендикулярных плоскостях. Однако построение численных алгоритмов непосредственно на основании этой формулы, затруднительно. Дело, в частности, в том, что формула обращения основана на преобразовании Фурье от однородной функции, получаемой из исходных данных. Причем преобразование Фурье понимается в смысле обобщенных функций, а преобразование Фурье в обычном смысле может не существовать. В настоящем параграфе приводятся выражения для используемого преобразования Фурье, позволяющие при построении численных алгоритмов использовать метод, изложенный в предыдущем параграфе. Устанавливаются также некоторые соотношения между результатами
Пустьзаданыфункцияf (x ) = f (x 1 , x 2 , x 3 ) , точкаS = (s 1 , s 2 , s 3 ) ивекторa = (a 1 , a 2 , a 3 ). Лучевым преобразованием функции f (x ) будем называть функцию
,
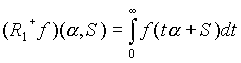являющуюся интегралом от f (x ) вдоль луча, исходящего из точки S в направлении вектора a .
Наряду с функцией 
в некоторых ситуациях рассматривается функция
,
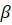являющаяся интегралом по всей прямой или, что тоже самое, суммой интегралов вдоль лучей из точки z в направлениях a и -a .
Множество точек S , для которых известно лучевое преобразование обычно является множеством точек, принадлежащих некоторой кривой, являющейся траекторией движения источника излучения.
Пусть задана кривая, по которой движется источник, Ф(l ) = (Ф1 (l ), Ф2 (l ), Ф3 (l )) параметр l пробегает некоторый интервал Ù действительной прямой. Для любого a = (a 1 , a 2 , a 3 ) и l Î Ù определим функцию
.
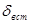Функция g(a ,l ) есть интеграл от функции f
(x
) вдоль проходящего через точку Ф(l ) в направлении вектора a . Отметим, что при любом фиксированном l функция 
является l однородной функцией a степени -1:
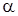. (2.1.1)
Для функций, имеющих финитный носитель, в [101] получена формула:
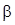. (2.1.2)
При фиксированном l функция G+
(b ,l ) есть преобразование Фурье от функции по переменной a , b = (cosq cosf , sinq cosf , sinf ). В формуле (2.1.2) l зависит от x и b и выбирается из условий: скалярное произведение (b , x) равно (b ,f (l )), но (b ,Ф(l )) не равно нулю. Значение функции f
(x
) может быть восстановлено в точке x
, если такое l существует для любого b . Геометрически это означает, что любая плоскость, пересекающая точку x
носителя функции, пересекает кривую Ф(l ) так, что знаменатель в (2.1.2) не обращается в нуль. Примером кривой, удовлетворяющей условиям Кириллова-Туя, является совокупность двух единичных окружностей, лежащих во взаимно перпендикулярных плоскостях, если носитель лежит в единичном шаре. Для цилиндрических объектов можно использовать винтовую линию.
В формулу (2.1.2) входит G+
(b ,l ) - преобразование Фурье от функции , однако преобразование Фурье, понимаемое в обычном смысле:
,
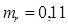в данном случае не существует, так как является однородной и имеет на бесконечности порядок 1/ê a ê . Преоразование Фурье здесь понимается в смысле обобщенных функций. Поскольку однородная функция, то при любом фиксированном l исходные данные, полностью определяются своими значениями на поверхности ê a ê =1. Переход к функции, заданной во всем пространстве R3
при использовании преобразования Фурье приводит к обобщенным функциям. Преобразование Фурье в
9-09-2015, 00:20