задается с помощью регулярной функции и иметь для нее выражения через функцию 
. В работе [101] дается выражение, связывающее , при x отличном от нуля с помощью регулярных операций с искомой функций f
(x
), то есть фактически показано, что функционал задается с помощью регулярной функции. Однако для построения алгоритмов томографической реконструкции нужно выразить не через искомую функцию f
(x
), а через исходные данные .
Итак, перейдем к нахождению . Мы будем использовать то, что является однородной функцией по a фиксированном l . В [95] доказано следующее
Утверждение
: Пусть 
есть преобразование Фурье в смысле обобщенных функций от однородной функции 
, тогда
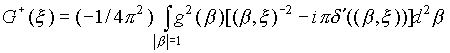. (2.1.3)
Строгое доказательство требует существенного использования аппарата обобщенных функций, понимаемых как линейные функционалы над соответствующим пространством. Здесь мы ограничимся изложением основных моментов доказательства. В частности, замену переменных в расходящихся интегралах мы будем делать по тем же правилам, что и в обычных.
Представим в виде
,
(поскольку параметр l фиксирован, его на данном этапе можно опустить).
Как уже отмечалось выше, интеграл является расходящимся, тем не менее, переходя к сферическим координатам по обычным правилам, получаем:
,
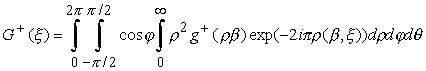где b = b (j ,q ) = (cosq cosj , sinq cosj , sinj ), j Î [-p /2, p /2], q Î [0, p ].
Учитывая, что 
, а также то, что интегрирование по углам j и q соответствует интегрированию по единичной сфере, приходим к выражению
.
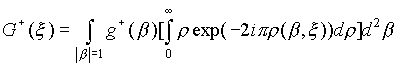Интеграл по r есть преобразование Фурье от r + +. Используя таблицы для преобразования Фурье обобщенных функций [19], приходим к выражению (2.1.3).
Для действительных функций f
(x
) в формуле (2) нужна мнимая часть :
.
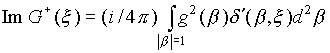Используя обобщенные функции, сосредоточенные на поверхности [19], получаем следующее следствие:
.
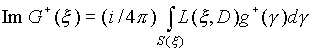Здесь S
(x ) = {g Î S
2
½
(x , g ) = 0),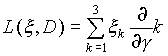 
v производная по направлению x . Подставляя в (2.1.2) функции 
и 
, зависящие от параметра l , получаем формулу обращения, пригодную для построения численных алгоритмов:
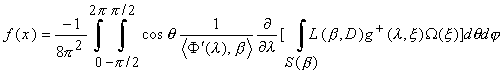(2.1.4)
Здесь S
(x ) v окружность, являющаяся пересечением единичной сферы и плоскости P(b ). Плоскость P(b ) проходит через начало координат ортогональна вектору b . Символ W (x ) означает интегрирование по окружности. Оператор L
(b , D
) означает дифференцирование функции в направлении вектора b :
,
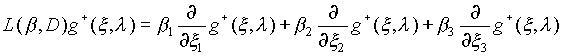при этом l , зависящее от b и x , остается фиксированным.
Как и выше, b = b (q , j ) = (cosq cosj , cosq sinj , sinq ), l = l (q , j ) = l (x , b ) такое, что скалярное произведение (x , b ) равно (b , g (l )) и (b , g / (l )).
В формуле (4) используются регулярные функции, и она пригодна для построения численных алгоритмов.
Замечание . А.С. Денисюком независимо и другим методом, без явного использования преобразования Фурье обобщенных функций, получены формулы обращения функции g + в Rn . При n = 3 формулы А.С. Денисюка и формулы, получаемые изложенным способом из формулы Туя, совпадают.
Выше были получены формулы, позволяющие строить численные алгоритмы восстановления функции f (x ) = f (x 1 , x 2 , x 3 ) по ее лучевому преобразованию
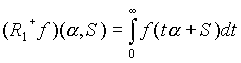
Далее мы будем опускать символ f
и использовать обозначение 
.
При фиксированном S
функция 
является функцией в трехмерном пространстве, но в силу ee однородности существуют поверхности, такие что 
полностью определяется своими значениями на них (поверхности расположения приемников излучения).
Исходные данные в виде функции 
удобно использовать, если матрица приемников расположена на сфере. Однако в реальных ситуациях матрицу приемников обычно располагают на плоскости или поверхности цилиндра. В этих случаях удобно использовать несколько иной вид исходных данных.
Плоский детектор.
Мы будем предполагать, что для источника, находящегося в точке S = (s1 , s2 , s3 ), исходные данные регистрируются в плоскости P, определяемой уравнением x s1 + y s2 + z s3 = -½S ½ . Плоскость P, определяется следующими условиями:
плоскость P перпендикулярна лучу, соединяющему источник с началом координат;
плоскость P проходит через точку S = (s1 , s2 , s3 .)
Расстояние D между плоскостью регистрации и источником равно удвоенному расстоянию от источника до начала координат. В плоскости регистрации будем использовать прямоугольную систему координат (p 1 , p 2 ), начало которой находится в точке пересечения с лучем, соединяющим источник с точкой (0, 0, 0). Таким образом, если источник находится в точке S = (s1 , s2 , s3 ), то начало системы координат (p 1 , p 2 ) в плоскости наблюдения находится в точке с трехмерными координатами -s1 , -s2 , -s3 = - S.
При реконструкции в конусе лучей наиболее распространенными примерами траекторий источника являются винтовая линия и совокупность двух окружностей лежащих в пересекающихся плоскостях.
Траектория в виде двух окружностей.
Рассмотрим окружность, лежащую в плоскости z =0.
Направление оси p 2 в плоскости регистрации будет совпадать с направлением оси z .
Ось p 1 системы координат возьмем на линии пересечения плоскости регистрации с плоскостью, содержащей окружность, по которой движется источник. Для окончательного определения системы координат необходимо выбрать одно из двух возможных направлений оси p 1 . Если s3 = 0, s1 = r cosl , s2 = r sinl (источник движется в плоскости z =0), то положительный единичный вектор на оси p 1 выберем так, чтобы он совпадал с вектором (cos(l +p /2), sin(l +p /2), 0) = (-sinl , cosl , 0) = (-s2 /½S ½ , s1 /½S ½ , 0).
Точка, имеющая в плоскости регистрации координаты (p 1 , p 2 ), имеет следующие пространственные координаты:
x = -p 1 sinl - r cosl = -p 1 s 2 /½S ½ - s 1 ,
y = p 1 cos l - r sinl = p 1 s 1 /½S ½ - s 2 , z = p 2 .
В случае плоского детектора, исходными данными являются интегралы по лучам, соединяющим точки (p 1 , p 2 ) в плоскости регистрации с источником S .
Регистрируемая функция gr (p 1 , p 2 , l ) есть интеграл от искомой функции f (x ) = f (x 1 , x 2 , x 3 ) вдоль луча исходящего из точки S = (s1 , s2 , s3 ) = (r cosl , r sinl , 0) в направлении точки
P = (-p 1 sin l - r cosl , p 1 cosl - r sinl , p 2 ) = (-p 1 s 2 /½S ½ v s 1 , p 1 s 1 /½S ½ v s 2 , p 2 ).
Интегральная форма регистрируемой функции имеет вид:
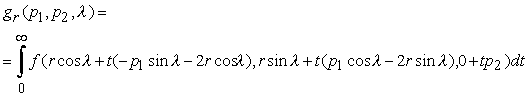
При t = 0 луч проходит через точку S = (r cosl , r sinl , 0), при t = 1 v через точку P = (p 1, p 2 ) = (-p 1 sin l - r cosl , p 1 cosl - r sinl , p 2 ).
Итак, мы имеем соотношение между функциями gr
(p
1
, p
2
, l ) и 
:
,
.
Наряду с обозначением gr
(p
1
, p
2
, l ), мы будем использовать обозначения gr
(p
1
, p
2
, S
(l )), gr
(p
1
, p
2
, S
) и gr
(P
, S
) , здесь S
(l ) точка на траектории источника, соответствующая параметру l , P
= (p
1
, p
2
). Мы выразили функцию gr
(p
1
, p
2
, l ) через функцию = g
+
(x , l ).
В формуле обращения лучевого преобразования используется функция g
+
(x , l ) = для того, чтобы использовать gr
(p
1
, p
2
, l ), регистрируемую в случае плоского детектора, нужно выразить g
+
(x , l ) используя gr
(p
1
, p
2
, l ).
Для дальнейшего нам потребуются координаты (p 1 , p 2 ) (в системе координат плоскости регистрации) точки пересечения плоскости регистрации данных с лучем (S +tx ) = (s1 + tx 1 , s2 + tx 2 , s3 + tx 3 ). Эти координаты имеют вид:
.
.
Теперь мы можем выразить используя gr
(p
1, p
2, l ):
= g
+ (x , l ) = gr
(2 ½S
(l )½ (s2(l )x 1 v s1(l )x 2) /
, -2½S
(l )½ 2x 3 /,l ),
если 
< 0, = 0, если ³0.
Итак, мы имеем следующее соотношение между функциями:
g
+ (P, l ) и = g
+ (x , l ); P = (p
1, p
2), x = (x
1, x 2, x 3,);
= g
+ (x , l ) =
= gr
(2 ½S
(l )½ (s2(l )x 1 v s1(l )x 2) /, - 2½S
(l )½ 2x 3 /,l ),
если < 0,
= 0, если ³ 0.
При переходе от функции g
+ (x , l ) = к функции g
r (P, S
) интегрирование по окружности S
(l ) в трехмерном пространстве заменяется на интегрирование по прямым линиям в плоскости регистрации. Отметим, что формулы обращения лучевого преобразования, использующие интегрирование вдоль прямых в плоскости регистрации.
4.3 Элементы теории обобщенных функций в применении к задачам обращения лучевого преобразования
Обобщенная функция это непрерывный линейный функционал на пространстве К всех функций a (x ), имеющих производные всех порядков и финитный носитель (свой для каждой из функций α (x )). Любая регулярная интегрируемая функция f (x ) задает линейный функционал (f, a ):
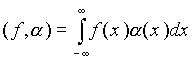. (2.2.1)
Однако на пространстве функций K существуют непрерывные линейные функционалы, которые не могут быть заданы с помощью регулярных интегрируемых функций, наиболее известными примерами таких функционалов являются δ-функция и ее производные. Другим широко известным примером является функционал, основанный на функции (1/x) d x. Функция 1/x x является регулярной, однако она не является интегрируемой. При задании соответствующего функционала интеграл
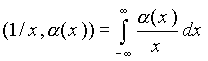(2.2.2)
понимается в смысле главного значения:
.
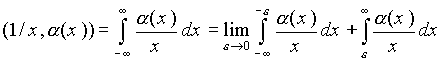Такое понимание интеграла используется при определении преобразования Гильберта от функции α (x ) как свертки с функцией 1/x x.
.
Преобразование Гильберта используется, в частности, в одной из формул обращения преобразования Радона в двумерном пространстве. Эта формула обычно приводится в руководствах по компьютерной рентгеновской томографии. Однако метод свертки и обратного проецирования, часто используемый при построении численных алгоритмов томографической реконструкции, основан на несколько другом виде формулы обращения преобразования Радона. В этом методе по существу используется свертка проекционных данных последовательностью функций сходящихся к 1/x x2 в смысле обобщенных функций.
Линейный функционал, соответствующий функции 1/x x2 , или, что то же самое, обобщенная функция 1/x x2 определяется формулой [19]
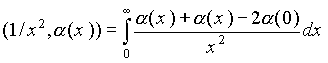(2.2.3)
Интеграл в (2.2.3) сходится в обычном смысле для любой функции a (x ) из пространства основных, и даже из более широкого класса, функций.
В формулах обращения преобразования Радона используется свертка данных с функцией 1/x x2 . Свертка обобщенных функций определяется следующим образом.
Пусть заданы два функционала f и g . Действие функционала f *g являющегося их сверткой, на функцию a из пространства основных задается формулой
(f *g , a )= (f x , g y , a (x + y ))). (2.2.4)
Здесь g y означает, что функционал действует на функцию a , как функцию переменной y , а функционал f действует на полученную функцию переменной x . Если функционалы f и g можно задать регулярными функциям, то функционал свертки определенный формулой (2.2.4) можно задать функцией, являющейся сверткой соответствующих функций в обычном смысле.
Здесь следует сделать одно замечание. Даже если функция одной переменной a (t ) имеет финитный носитель, функция двух переменных a (x + y ) не является функцией с финитным носителем. Это означает, что существование функционала f *g для конкретных функционалов f и g или необходимо доказывать. Известно, что для существования функционала свертки, достаточно, чтобы один из функционалов имел финитный носитель.
Если рассматривать задачи томографии, то там с функцией 1/x x2 сворачиваются исходные данные, которые регулярны и имеют финитный носитель. Можно показать также, что необходимая свертка выражается формулой:
S (r , j ) = I (r , j ) * (-1/pr 2 ) =
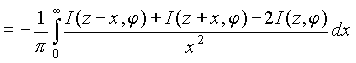(2.2.5)
В реальных ситуациях функция I (r , j ) известна в некотором дискретном множестве точек. Для того, чтобы использовать формулу (2.2.4) нужно построить аппроксимацию функции I (r , j ), такую что интеграл в правой части имеет смысл. Интеграл (2.2.4) заведомо сходится, если функция I (r , j ) принадлежит множеству K, то есть имеет финитный носитель и является бесконечно дифференцируемой.
Однако аппроксимация данных бесконечно дифференцируемой функцией может оказаться громоздкой при построении численных алгоритмов. Кроме того, использование бесконечно дифференцируемых функций может приводить к заглаживанию границ областей с резко отличающимися плотностями. Для сходимости интеграла в (2.2.5) достаточно, чтобы функция I (r , j ) имела в каждой точке конечные односторонние производные первого порядка по переменной r . Это позволяет, в частности, использовать кубические сплайны для построения аппроксимации функции I (r , j ).
Основными операциями с обобщенными функциями, используемыми в задачах томографии, являются свертка, дифференцирование и преобразование Фурье. Основная идея определения операций заключается в том, что некоторые свойства функционалов, задаваемых регулярными функциями, берутся за основу при определении соответствующих операций над обобщенными функциями, являющимися линейными функционалами.
На этой основе построено приведенное выше определение свертки. Особенно просто и наглядно этот прием можно продемонстрировать при определении операции дифференцирования обобщенных функций.
Пусть линейный функционал f задается регулярной функцией f (x ) имеющей интегрируемую производную. Для действия производной на функцию a (x ) из пространства основных можно записать равенство
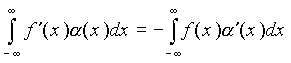, (2.2.6)
здесь использовано интегрирование по частям и то, что a (x ) равна нулю вне некоторого конечного интервала.
Приведенное выше свойство берется за основу при определении производной обобщенной функции. Пусть задан функционал f
, его производной называется функционал f
/
, определяемый равенством 
. Так как функции из пространства основных бесконечно дифференцируемы, то определение является корректным и обобщенные функции имеют производные любого порядка.
Перейдем к определению преобразования Фурье в смысле обобщенных функций. В приводившихся выше определениях функции, входящие в пространство основных, были действительными. При определении преобразования Фурье целесообразно в качестве основных рассмотреть комплекснозначные функции.
Пусть K пространство комплексных основных функций (бесконечно дифференцируемых с финитным носителем).
Каждой комплекснозначной локально интегрируемой функции f (x ) ставится в соответствие функционал
,
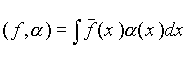комплексно сопряжена с f
(x
), a (x
) Î K.
Множество всех линейных непрерывных функционалов на K образует комплексное пространство обобщенных функций K/ . Обозначим через Z - множество функций, являющихся преобразованиями Фурье функций из K.
Преобразованием Фурье элемента f из пространства K называется функционал g на пространстве Z , действующий по формуле
(g , y ) = 2 p (f , a ), (2.2.7)
здесь j такой элемент из K, для которого преобразование Фурье есть y . То есть для того чтобы вычислить действие функционала g на функцию y (l ) из пространства Z , нужно:
найти такую функцию a (x ) из пространства K, преобразованием Фурье, которой является функция y (l );
найти действие функционала f на найденную функцию a (x ).
Пространства основных функций и функционалов над ними выбраны нами так, что оба шага всегда выполнимы.
Здесь следует обратить внимание на то, что обобщенные функции и их преобразования Фурье определяются как линейные функционалы над разными основными пространствами. Причем функции из множества Z, на котором действуют преобразования Фурье, не являются функциями с финитными носителями, но продолжают оставаться бесконечно дифференцируемым. Что позволяет сохранить многие полезные свойства обобщенных функций.
В формулах обращения лучевого преобразования, на которых основаны алгоритмы решения задачах трехмерной компьютерной томографии,
9-09-2015, 00:20