Болдов Илья Александрович
Введение
Существующие теории строения элементарных частиц, как правило, не рассматривают частицы как протяженные объекты, имеющие какую-либо внутреннюю структуру. Между тем, логично было бы предположить, что масса частиц зависит от ее пространственной протяженности, а точнее, объема. Это предположение также подкрепляется гипотезой “Большого взрыва”, по которой вся видимая вселенная образовалась практически одновременно. Скорее всего, можно говорить о том, что плотность вещества в широком понимании, т.е. частиц, которые принято называть “элементарными”, и которые появились одновременно, одинакова в рамках наблюдаемой реальности. Это предположение о равномерной плотности частиц и их определенных размерах, легло в основу предлагаемой “геометрической теории”.
Современные методы изучения строения элементарных частиц, заключающиеся в их разгоне на ускорителе, и разбивании о мишень, можно сравнить с изучением строения условного камешка, путем его разгона до субсветовых скоростей, разбивания его о стену, и исследования полученных обломков. Безусловно, многие достижения в изучении элементарных частиц принадлежит именно таким методам. Но причисление к числу “элементарных” все бỏльшего количества частиц, резонансов, бозонов, дает повод считать, что либо не все они истинно “элементарные”, либо критерий их отбора необходимо менять, либо как-то объяснить существующее положение вещей простым и понятным способом.
Опыты Хофштадтера по рассеянию быстрых электронов на атомных ядрах убедительно показали, что нуклоны имеют конечные пространственные размеры. Но поскольку элементарным частицам с самого начала было отказано в праве иметь пространственную структуру, то и попыток классификации с ее помощью не было.
Размеры радиусов нуклонов (протона и нейтрона) в 0,8 Ферми (1Ф = 10–13 см) найдены Хофштадтером экспериментально, поэтому не могли быть отвергнуты и зафиксированы в справочниках (как досадное исключение, на которое никто не обращал внимания). Таким образом, есть два принципиально различных подхода к описанию структуры элементарных частиц: либо локальность, теория относительности и принцип неопределенности Гейзенберга, либо протяженность и отказ от теорий, которые ей противоречат.
В настоящее время, по каким-то причинам, всеобщее признание получила теория, согласно которой частицы – есть кванты или возбужденные состояния некоего абстрактного поля. Понятно, что все это есть попытки достичь “Святого Грааля” современной физики – создать Единую Теорию Поля, и одним уравнением описать сильное, слабое, электромагнитное и гравитационное взаимодействие частицы. В безрезультатной погоне за этой мечтой физика элементарных частиц находится уже около полувека. В результате подгонки теории под наблюдаемые факты, придумываются очередные навороты и несуразности. Начинается вся эта каша корпускулярно-волновым дуализмом, т.е. утверждением, что частица одновременно является и собственно частицей (кусочком материи с некоей массой), и волновым процессом, т.е. колебанием неких полей, которые также являются видом материи. Далее, пытаясь объяснить некие факты, было сделано предположение, что частицы состоят из неких “кварков” в количестве трех штук, потом у этих “кварков” появились “странность”, “очарование”, “цвет”, “изотопический спин” и количество их выросло за два десятка.
Какие-то из этих теорий находили подтверждение в опытах, какие-то пока остаются только на бумаге. Так до сих пор не найдены те самые “кварки”. И самое главное- нет НИ ОДНОЙ теории способной хоть как-то дать внятное объяснение значениям масс элементарных частиц.
А поскольку общепринятая “полевая” теория также противоречит неким упрямым фактам (о размерах частиц), наверное стоит поискать смысл и истину в другом месте.
Строение элементарных частиц
Из курса физики в объеме средней школы известно, что полная энергия частицы в инерциальной системе отсчета Еин равна сумме энергии покоя Е0 и энергии движения Е имп.
Еин= Е0 + Е имп, (1)
где
Е0 = m c2 (2)
В момент удара частицы о мишень можно говорить об ее эквивалентной массе, определяемой как :
m = Еин / c2 (3)
При разгоне частиц до субсветовых скоростей прирост массы весьма значителен, что позволило наблюдать частицы с массой намного больше чем масса протона. Если сравнивать все это с попытками исследования условного камешка, то в момент удара о стену он превращается в огромный булыжник, и разлетается на куски, масса которых намного больше массы покоя исходного камешка.
Именно это и ввело исследователей элементарных частиц в заблуждение, что куски, на которые разлетается исходная частица (протон), также являются самостоятельными (родившимися?) частицами, хотя совершенно непонятно, что дало повод считать именно так. Отличие свойств от свойств исходных частиц? Но один из основополагающих гносеологических законов философии - Закон перехода количества в качество. Да, свойства изменились, но это всего лишь потому, что изменилось количество материи. А то, что получается в результате столкновения двух релятивистских протонов, не может быть ничем иным, кроме многократно увеличенных частей (кусков) протона, и тех продуктов, на которые эти части распадаются далее. А поскольку часть не равна целому, то и свойства у полученных кусков иные. Масса полученных частиц большая ? Так затем и разгоняли, чтобы масса увеличилась.
Сам термин “рождение” частицы по смыслу подразумевает то, что вот ничего не было, а вот стало. Частица “родилась”. Возникают резонные вопросы - Из чего родилось ? И куда делось то, что было ? Умерло ? Ушло в небытие ?
Но еще г-ну Ломоносову был известен закон сохранения вещества. Может быть более правильным говорить о “превращении” частиц или их кусков ? Об их видоизменении, разделении на части или соединении в целое ?
И тут всего один шаг до вывода, что если частицы или их части могут “превращаться” друг в друга (соединяться и разделяться), то все они состоят из одной какой-то материи (как философской категории), которая может принимать различные формы. Вот тогда все встает на свои места. Причем в данном случае термин “формы” имеется в виду, как в натуральном, геометрическом, так и в философском значении.
Тут стоит вспомнить еще об одном законе философии – Законе диалектической связи между формой и содержанием. А поскольку содержание и свойства неразрывно связаны, то изменение формы ведет к изменению содержания, и соответственно свойств.
Именно поэтому попытки систематизировать и как-то объяснить все известные “элементарные частицы” не удаются, поскольку физики неправильно понимают, что именно они исследуют, сваливая в одну кучу как собственно “элементарные” частицы, так и их осколки. Именно потому количество разновидности того, что физики получают на ускорителях, растет, что с ростом энергии разгона частиц, получается больше разных осколков с совершенно разными формами и соответственно с различными свойствами.
С этой точки зрения, можно считать всю современную физику элементарных частиц вкупе с квантовой хромодинамикой, науками по изучению и систематизации осколков увеличенных нуклонов и ничем более.
В данном случае мы имеем ярчайший пример как неправильный термин, уводит от истинного смысла явления.
Еще в 1917 г. П. Эренфест отметил, что в эвклидовых пространствах с размерностью более трех не могут существовать устойчивые аналоги атомов и планетных систем. Но, поскольку при размерности менее трех не могут возникнуть сложные структуры, то три является единственной размерностью, при которой реализуются основные, устойчивые элементы Вселенной, т.е. элементарные частицы.
Логично было бы предположить (применив “Принцип Оккама”), что и элементарные частицы существуют в трехмерном виде и только. Следовательно, все свойства, и в первую очередь масса, этих частиц определяются только их строением и объемом в нашем трехмерном мире.
Из теории групп известно, что конечные подгруппы собственных вращений трехмерного пространства исчерпываются списком: Cn, Dn , C , O, Y
В списке имеется две серии Cn, Dn с произвольным n. Остальные C , O, Y – спорадические группы симметрии правильных многогранников, которые не входят ни в какие серии.
Если рассмотреть таблицу правильных выпуклых многогранников (тел.Платона), все грани которых есть конгруэнтные правильные многоугольники, то можно заметить ее сходство с началом таблицы элементарных частиц.
Таблица 1. Правильные выпуклые многогранники
№ пп |
Вид многогранника | Граней | Вершин | Ребер |
| 1 | Тетраэдр | 4 | 4 | 6 |
| 2 | Октаэдр | 8 | 6 | 12 |
| 3 | Гексаэдр (куб) | 6 | 8 | 12 |
| 4 | Икосаэдр | 12 | 20 | 30 |
| 5 | Додекаэдр | 20 | 12 | 30 |




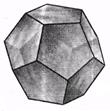
Тетраэдр Октаэдр Гексаэдр Икосаэдр Додекаэдр
Рисунок 1. Правильные многогранники
Таблица 2. Фотон и Лептоны
№ пп |
Вид частицы | Масса, Мэв | Электр. Заряд | Лептон. Заряд Вид заряда |
| 1 | γ | ~ 0 | 0 | 0 |
| 2 | ν e | < 7*10-6 | 0 | +1 e |
| 3 | e- | > 4.3*1023 лет | -1 | +1 e |
| 4 | ν μ | < 0.17 | 0 | +1 μ |
| 5 | μ - | 2.2*10-6 | -1 | +1 μ |
Выскажем гипотезу:
Элементарные частицы представляют собой по форме многогранники. Масса частицы определяется объемом соответствующего многогранника и зависит от длины ребра. Свойства частицы определяются видом (структурой) многогранника. Проявления различных законов сохранения нефизических зарядов (лептонных, барионных, странность и пр.) - следствия закона сохранения структуры многогранника, выраженной в его осях симметрии. При столкновении частиц их многогранники соединяются в (или раскалываются на) частицы , которые принимают форму иных многогранников.
Как видим из Таблицы 1, есть две группы многогранников, которые дуальны, т.е один можно получить из другого, если центры граней одного, принять за вершины другого, и которые имеют одинаковую симметрию. Это пары Гексаэдр и Октаэдр, Додекаэдр и Икосаэдр. У каждой из этих пар одинаковое количество ребер, а количество вершин и граней меняются местами. Можно предположить, что это пары связанные лептонными зарядами, тогда первая пара – это Электрон (Гексаэдр или Куб) и электронное нейтрино (Октаэдр). Вторая пара – Додекаэдр (Мюон) и Икосаэдр (Мюонное нейтрино).
Также есть один многогранник, который дуален сам себе. Это тетраэдр. В таблице 2 ему соответствует Фотон.
Сделав такое предположение, можно заметить, что частицы, многогранники которых, образованы из правильных треугольников, движутся со скоростью света. У автора пока нет этому объяснения. Напротив, многогранники, образованные из квадрата (Электрон) и пятиугольника (Мюон), имеют массу покоя.
Объем Гексаэдра определяется как третья степень длины его стороны а. Приняв сторону Гексаэдра за единицу, получим:
Vе = а3 = 1: (4)
Объем Додекаэдра при стороне равной а определяется по формуле :
V μ = a3/4(15+7√5); (5)
Приняв сторону Додекаэдра а=3, получим:
V μ =206,9.
Если сравнить полученную величину с общепринятой величиной массы Мюона (в электронных массах) равной 206,77, то увидим, что погрешность определения массы Мюона по новой теории, составляет менее семи сотых процента, что вполне неплохо, и не может объясняться простым совпадением.
Лептонный заряд можно объяснить дуальностью частиц или, точнее, одинаковым количеством и расположением осей симметрии. В Табл. 1 это электронный лептонный заряд и мюонный лептонный заряды, соответственно.
Распад Мюона, согласно предложенной гипотезе, представляется как “схлопывание” Додекаэдра в Куб, Икосаэдр и Октаэдр.
| Частица | µ- | е- | ν e | ν μ | Разница |
| Грани | 12 | 6 | -8 | 20 | 12 - (6-8+20 ) = 6 |
| Вершины | 20 | 8 | -6 | 12 | 20 - ( 8 -6+12) = - 6 |
| Ребра | 30 | 12 | -12 | 30 | 30 - (12-12+30) = 0 |
При этом появляется шесть новых граней, а шесть вершин пропадают. Логично предположить, что при распаде мюона, шесть вершин развернулись в шесть граней. При этом Мюонное нейтрино сохранило оси симметрии Мюона, Электрон получил электрический заряд, а появившиеся оси симметрии Электрона компенсируют оси симметрии Электронного антинейтрино.
Отдельно стоит отметить то, что представление электрона в виде куба объясняет строение молекул. Если куб представить в виде вектора, проходящего из одной вершины в другую через центр, то количество возможных положений вектора в трехмерном пространстве будет равно восьми. Следовательно, электрон может находиться в определенной области пространства в восьми возможных положениях, что равно максимальному количеству электронов в общих валентных оболочках атомов, связанных в молекулу.
Конечно, в Табл. 2 отсутствуют еще два Лептона: это Тау –лептон, и его нейтрино. Поскольку первый лептон – Электрон, состоит из граней с четырьмя сторонами, второй лептон – Мюон, из граней с пятью сторонами то, многогранник Тау-лептона должен состоять из правильных шестиугольников, а Тау-нейтрино, соответственно из правильных треугольников, причем оба многогранника должны быть дуальны..
Но других правильных выпуклых многогранников больше нет. Да, и составить многогранник, состоящий только из правильных шестиугольников невозможно. Видимо, следует обратить внимание на иные многогранники, а именно выпуклые Параллелоэдры (Тела Федорова). И среди них мы заметим Гексагон, многогранник, представляющий собой прямую призму с правильным шестиугольником в основании, и высотой, равной, стороне шестиугольника и дуальный ему Додекатетр, похожий на Октаэдр, только граней у вершины шесть и грани представляют собой равнобедренные треугольники с основанием равным √3/2 от длины боковой стороны.
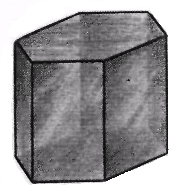

Рисунок 2. Гексагон и Додекатетр
Если Гексагон – Тау-мезон, то Додекатетр – Тау-нейтрино. Объем Гексагона со стороной равной а определим как:
V τ = √3*3/2*а3 (6)
При стороне а = 11 получим :
V τ =3 458,04. (7)
Если сравнить полученную величину с общепринятой величиной массы Тау-мезона (в электронных массах) равной 3 477,50 то увидим, что погрешность определения массы в данном случае менее шести десятых процента, что также не может объясняться простым совпадением.
Логично предположить, что поскольку правильные многогранники исчерпаны, то другие элементарные частицы представляют собой иные многогранники.
Следующими рассмотрим полуправильные многогранники, представляющие собой правильные многогранники, симметрично усеченные.
Первым на такую операцию усечения объема рассмотрим тетраэдр.
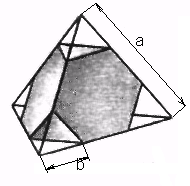
Рисунок 3. Усеченный Тетраэдр
Объем такого тела будет определяться как разность объема исходного тетраэдра со стороной равной а, и объема четырех отсеченных тетраэдров со стороной b.
V = (√2)/12 * a3 - 4*(√ 2)/12 * b3 (8)
Безусловно, возможны много вариантов с различными значениями a и b.
Среди них мы отметим вариант, когда а = 14, b = 5, при этом V =264,48. По полученному результату, это - Пи-0 мезон. Его масса равна 264,15 е.м.
Следующим рассмотрим “усеченный куб” (Рис. 4)
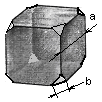
Рисунок 4. Усеченный Куб
Его объем определится как объем исходного куба со стороной а, за минусом объема восьми отсеченных углов со стороной b. Заметим, что отсеченные углы составляют октаэдр со стороной b.
V = a3 - √2/3 b3. (9)
Приняв а = 6,5 b = 1,0, получим V =274,154. По полученному результату, это Пи+ /- мезон. Его масса равна 273,39 е.м.
Отметим, что оставшаяся часть ребра составляет 6,5- √2 ≈ 5.
Все массы частиц, о которых шла речь до сих пор – это так называемая масса покоя. Она вычислялась как функция от длины стороны. Отдельного разговора достойны четыре частицы, движущиеся со скоростью света, и масса которых определяется из классической формулы E = mc2. Это фотон и три вида нейтрино. Для этих частиц проведем обратное преобразование – получим длину стороны многогранника от известной массы. Массу фотона примем равной нулю, а за единицу примем длину грани Гексаэдра (Электрона). Тогда длина грани Электронного нейтрино будет равна 0,030744. Длина грани Мюонного нейтрино равна 0,53425016, а для Тау-нейтрино получим величину равной 3,43906451.
Сведем полученные результаты в таблицу. Причем в лептонах сгруппируем отдельно нейтрино и собственно лептоны.
Таблица 3. Сводная таблица Геометрии элементарных частиц
№ пп |
Вид частицы | Вид многогранника | Длина Грани |
Масса э.м. | Объем | Погрешность |
| 1 | γ | Тетраэдр | 0 | |||
| Лептоны | ||||||
| 2 | ν e | Октаэдр | 0,030744 | < 7 *10-6 | ||
| 3 | ν μ | Икосаэдр | 0,53425 | <0.17 | ||
| 4 | ν τ | Гексагон | 11 | <18 | ||
| 5 | e - | Гексаэдр | 1 | 1 | 1 | 0 |
| 6 | μ - | Додекаэдр | 3 | 206.77 | 206.9 | 0.062 % |
| 7 | τ | Додекатетр | 11 * | 3 477.5 | 3 458.04 | 0.56 % |
| Мезоны | ||||||
| 8 | π 0 | Тетр. Усечен. | 14 ** | 264.15 | 264.50 | 0.134 % |
| 9 | π+/ - | Куб Усечен. | 6,5 ** | 273.39 | 274.154 | 0.281 % |
* Длина ребер сходящихся к вершинам.
** Взята длина ребер неусеченных многогранников.
Многообразием усеченных правильных, полуправильных и неправильных многогранников можно объяснить и все многообразие видов элементарных частиц.
Тогда разновидности “кварков” - скорее всего, лишь виды многоугольников, из которых составлены многогранники – частицы. Чем большее их количество задействовано в построении многогранника (как по площади, так по видам), тем больше объем полученного многогранника, и соответственно масса элементарной частицы, которую он представляет.
Среди множества частиц есть две относительно стабильные. Это электрон и протон.
Стабильность электрона определяется Законом сохранения количества осей симметрии, проявляющимся как закон сохранения лептонного заряда, и законом сохранения электрического заряда.
Логично предположить, что закон сохранения барионного заряда – есть проявление того же закона. У каждого из лептонов и мезонов имеется только один узел симметрии. Если есть многогранники, на которые может распасться частица с сохранением симметрии, и позволяет объем ее многогранника, то происходит ее распад.
Но, видимо, центров симметрии может быть более одного. Или в одном месте могут быть несколько центров симметрии и тогда, например, получаются усеченные многогранники – мезоны.
С этой точки зрения распад тяжелой частицы - есть изменение ее сложной симметрии, и приближение к простой симметрии легких частиц.
Исходя из этих посылок и полученных многогранников Пи- мезонов, попробуем получить структуру протона и нейтрона. Исходя из современных представлений, что нуклоны окружены виртуальными Пи-мезонами, а также, что протон и нейтрон легко превращаются друг в друга, сделаем предположение, что они имеют нечто единое, что в результате добавления многогранников – мезонов, собственно и определяет вид частицы – нуклона.
Ребра Пи – 0 и Пи +- мезонов имеют одно общее число =5. Грани их представляют собой трех и четырехугольники. Предположим, что общая часть нуклонов- есть многогранник, составленный из правильных треугольников и квадратов со стороной = 5.

Рисунок 5. Гедра
Из полуправильных многогранников этим условиям отвечает так называемая “Гедра”. Объем ее со стороной а определяется как сумма составляющих объемов.
V = a3 + 6*a3* √2+ 8* a3/(6*2*√2) +6* a3/2 (10)
При стороне а = 5, V = 1089,26;
Добавив к Гедре шесть кубов со стороной а=5 , получим следующую структуру.
Объем такой структуры определится как :
V = 7* a3 + 6*a3* √2+ 8* a3/(6*2*√2) +6* a3/2 (11)
При стороне а = 5, V = 1839,26; В данном случае, мы имеем частицу - протон, окруженную
29-04-2015, 05:12
