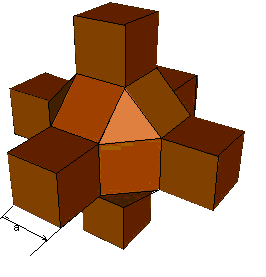
Рисунок 6. Протон
Масса нейтрона в свободном состоянии, как известно, больше массы протона. Простейший анализ атомарных весов по таблице периодической системы Д.И.Менделеева показывает, что в связанном состоянии – в ядре – масса нейтрона меньше массы протона и составляет 0,98÷0,99 от массы протона. При этом масса протона в ядре не меняется.
Попробуем объяснить, каким образом нуклоны связанны в ядре в единое целое, оставаясь при этом отдельными частицами. Если нуклоны в ядре имели бы соприкосновение вершинами, то такое соединение. видимо не имело бы большой жесткости, если же гранями, то можно предположить вероятность их “схлопывания” в одну частицу, или каким-то образом изменения их свойств. Жесткая конструкция, при сохранении собственной структуры, получается, если нуклоны имеют связь в ядре путем объединения ребер. Поскольку выступающие части многогранника – протона представляющие собой кубы, расположены под углом 90 градусов, то ответные грани выступающих частей нейтрона должны быть расположены так же. У Пи-0 мезонов, виртуально окружающих нейтрон, имеются грани – треугольники со стороной (?)=5. Видимо и соединение выступающих частей нейтрона приходится на грани треугольной формы.
Минимальное количество ребер необходимых для жесткого соединения двух многогранников (нуклонов) равно двум. Треугольных граней на Гедре – 8. Необходимо ли всем им иметь выступающие части? Нет, достаточно всего четырех, расположенных по вершинам вписанного в Гедру тетраэдра. Стороны такой усеченной пирамиды расположены под углами 90 º друг к другу, а внешняя сторона - правильный треугольник.
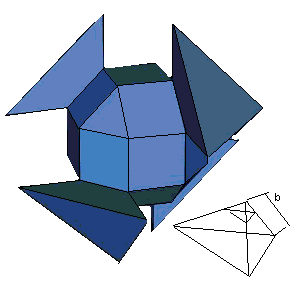
Рисунок 7. Нейтрон в ядре
При этом со всех шести сторон к нейтрону может быть присоединен протон двумя ребрами. Масса такой частицы определится как :
V = 7* a3 + 6*a3* √2+ 8* a3/(6*2*√2) +6* a3/2 + 4*( b3 –(a*√2)3)/6 . (12)
Здесь b = 10,5*√2; где 10,5 – длина грани от основания пирамиды со стороной b до вершины, спрятанной внутри Гедры. При а = 5, b=10,5 для нейтрона в ядре имеем:
V нейтр.связ.= 1831,54
В свободном состоянии, видимо, усеченные пирамиды будут стремиться к форме усеченного тетраэдра.
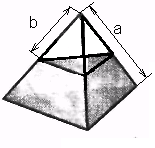
Рисунок 8. Усеченный тетраэдр
Объем усеченного теораэдра равен:
Vтетр.ус. =(√2)/12 * a3 - (√ 2)/12 * b3: (13)
Приняв а = 12, b = 5, получим объем пирамиды (виртуального Пи-0 мезона) для нейтрона в свободном состоянии:
V ус.тетр.= (√2)/12 * a3 1 (√ 2)/12 * b3 (14)
V ус.тетр.= 185,57
Масса нейтрона тогда определится как ;
V = a3 + 6*a3* √2+ 8* a3/(6*2*√2) +6* a3/2-(√2)/12 * a3 + (√ 2)/12 * b3 (15)
V нейтр. своб.= 1844,92
Сведем полученные результаты в таблицу.
Таблица 4. Нуклоны
№ пп |
Вид частицы | Вид многогранника | Длина Ребра |
Масса э.м. | Объем | Погрешность |
| 1 | Протон | Гедра + 6 кубов | 5 | 1836,14 | 1839,26 | 0,169 % |
| 2 | Нейтрон сободный | Гедра + 4 ус.пирамиды 90 º | 5+7 (10,5) |
1838,69 | 1844,92 | 0,339 % |
| 3 | Нейтрон в ядре | Гедра + 4 ус.пирамиды 60 º | 5+7 (12) |
1824,02 | 1831,54 | 0,412 % |
Согласно предлагаемой гипотезе, нуклоны в ядре будут связаны ребрами. При этом длина ребра усеченной пирамиды нейтрона, отходящей от Гедры, составляет около 7. Это на 2 больше, чем длина ребра выступающего куба протона. Таким образом, крайняя плоскость куба протона не достанет до Гедры нейтрона, и обе частицы сохранят свою структуру.
При распаде ядра, нейтрон оставляет четыре усеченные пирамиды, но они изменяют форму - превращаются в усеченные тетраэдры. Поскольку масса свободного нейтрона больше массы протона, то усеченные пирамиды опять преобразуются в кубы, и получается протон. При этом излишек вещества и отрицательный электрический заряд уносятся электроном и электронным нейтрино.
При разбивании протона в ускорителе о мишень он и частицы мишени распадаются на части - многогранники, ребра которых кратны длине ребра электрона. Поэтому массы получающихся частиц не образуют сплошной спектр значений, а подчинены определенной закономерности.
Тот факт, что все элементарные частицы в конечном счете (путем цепочек распада) превращаются (принимают форму) в правильные многогранники, или многогранники из них составленные, позволяет дополнить гипотезу следующим утверждением :
Тела Платона являются первичными элементарными формами, из которых состоят (частично или полностью) элементарные частицы. Форма неправильного многогранника частицы (или его частей) стремится принять форму тела Платона. Форма хотя бы одного из многогранников частиц получаемых при распаде, более близка к форме тел Платона, чем исходная частица.
Автор не берется пока объяснить, что именно является определяющим: свойства собственно “элементарной” частицы, плоскости граней, ребра или вершины.
Возможно, что вышеприведенное дополнение к гипотезе надо свести к не форме самого многогранника, а к виду его граней. Возможно, что ребра представляют собой некие струны – свертки пространства. Возможно, основой частицы (определяющей форму) является ее некий узел симметрии, который надо считать истинно “элементарным”. Все это требует дальнейшего осмысления.
Автор прекрасно понимает, что предложенная теория якобы противоречит общепринятому “дуализму” частиц. Поскольку частица с жестким объемом и структурой не укладывается в понятие “волна”. Все это справедливо, только если принять движение частицы математически непрерывным в каждой точке пространства с заданным жестким объемом. Под понятием точки, здесь понимается именно математическое определение, при котором расстояние между точками исчезающее мало, но не равно нулю. Но мы живем в реальном, а не математическом пространстве. В нем же движутся и элементарные частицы.
Давайте разберемся, что же это за “волновые” свойства. Во-первых, сам термин появился, когда допускалось существование некоего “эфира”, по которому распространялись световые “волны”. Во многом, сам термин обязан своему появлению эффекту дифракции, который объяснялся физиками чисто математически сложением неких волн- синусоид. С открытием фотона – с его корпускулярными свойствами, т.е. поведением его как частицы, при поглощении и испускании, ему же были переданы и волновые свойства световой волны, проявляющиеся при распространении. Так родился корпускулярно-волновой дуализм с оговоркой, что волновые свойства проявляются только при движении частиц.
В качестве объяснения проявления волновых свойств частиц, не противоречащих предложенному “геометрическому” устройству частиц, возможны как минимум два варианта.
Первый - “ячеистая” структура вакуума, где частицы могут находиться только в определенных “квантованных” местах пространства, “перескакивая” из одной ячейки в другую. В пользу такого объяснения говорит и наличие “туннельного” эффекта. При этом для осуществления движения необходима дополнительная кинетическая энергия.
Второй- это “осцилляция” самой частицы, то есть, “схлопывание” ее объема в точку ближайшей вершины, находящуюся по вектору движения частицы, и развертывание ее далее в полный объем на другом месте из этой же точки. Данное предположение ничем не экзотичнее корпускулярно-волнового дуализма.
Если при этом учесть вращение частицы (спин), то становится ясно, каким образом частица может двигаться в любом направлении трехмерного пространства. При этом вектор движения частицы, т.е. приложенная ей энергия движения, “размазывает” частицу (точнее ее осцилляции) в пространстве, образовывая “Волну де Бройля”.

Рисунок 9. Последовательные фазы осцилляции фотона
Так эффекты дифракции и интерференции можно объяснить, если считать светлые и темные полосы, видимые как результат попадания квантов света, не результатом сложения неких волн - синусоид, а как наглядно проявляемое распределение количества попадания фотонов (частиц) в определенные области пространства. Где-то густо (ярко), а где-то пусто (темно). Дифракция, как известно, наблюдается при прохождении волны (частицы) мимо края препятствия. При этом для наблюдения эффекта дифракции расстояние между частями препятствия должно быть сравнимо с длиной волны. При этом наблюдается краевой эффект. Но если принять хоть одно вышеприведенное объяснение “ячеистой” структуры вакуума, или “осцилляцию” частицы, то мы получим следующее:
1. Частицы, пролетающие вблизи от края препятствия, испытывают гравитационное притяжение к частицам препятствия. При этом вектор их движения получает смещение в сторону препятствия.
2. В силу “ячеистости” вакуума, или в результате “осцилляции” часть частиц не может образоваться (развернуться) в районе края препятствия и перескакивает в следующую за препятствием область пространства, по “туннельному” эффекту. Возможно, как вариант, “туннельный” перенос узла симметрии, который, развернувшись в частицу за краем препятствия, имеет широкий размах векторов движения.
3. Строение ядра
Предположим, что структура ядра однозначно отражается в структуре электронных оболочек атома, которые физиками достаточно хорошо изучены. В принципе возразить на это предположение нечего. Но в тоже время автору не известна ни одна попытка, составить структуру ядра так, как дети собирают игрушечную пирамидку из кубиков, на основании знаний об электронных оболочках атома.
Попробуем сделать это сообразно полученным выше выводам, что нуклоны в ядре соединяются в трехмерном пространстве под углами 90º. Причем не могут быть присоединены друг к другу два протона или два нейтрона. Только протон к нейтрону. Именно поэтому в ядре необходимы нейтроны в количестве не меньшем чем количество протонов, хотя известно и одно исключение – He3.
С этой точки зрения ядро Дейтерия представляет собой простейшую пару нуклонов из которой строятся ядро любого атома (Рис. 10).
![]()
n - p
Рисунок 10. Ядро Дейтерия
![]()
Рисунок 11.Ядро Гелия 4 (1 слой)
Как видим, первый сложный атом – Гелий, состоит из двух пар нуклонов первого слоя, которые лежат в одной плоскости (Рис.11).
Примем, что структура из двух пар нуклонов формирует S-структуру электронной оболочки атома. Мы также будем называть такую структуру из двух пар нуклонов – S-оболочкой ядра.
Очевидно, что прибавление еще одной пары нуклонов даст ядро Лития. Но прибавление этой пары происходит в S-оболочке второго слоя, которая находится рядом с S – оболочкой первого слоя.
1 слой
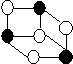
2 слой
Рисунок 12. Ядро Лития
Для дополнительной жесткости в структуру ядра Лития добавляется лишний нейтрон. Дальнейшее усложнение структуры ядра достигается добавлением нуклонных пар в плоскости второго слоя ядра вокруг S-оболочки и полностью заполняется еще шестью парами нуклонов. Примем, что эти шесть пар - P – оболочка.
При этом добавление происходит как с лишними нейтронами так и без.
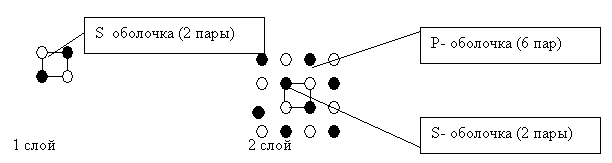
Рисунок 13. Послойная структура ядра Неона (1S2+ 2S2+ 2P6)
(Магическое число – 20)
Заметим, что S –оболочки находятся рядом друг с другом в соседних слоях.
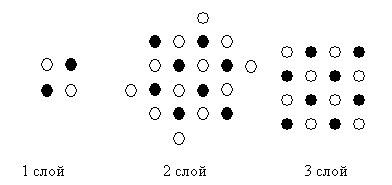
Рисунок 14. Послойная структура ядра Аргона (1S2+ 2S2 +2P6 + 3S2 + 3P6)
(Магическое число – 40, во втором (или третьем) слое – дополнительно 4 нейтрона)
Очевидно, что следующая оболочка в слое будет состоять максимум из десяти пар нуклонов.
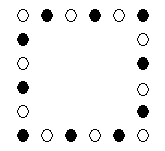
Рисунок 15. D-оболочка (10 пар)
Следующая в слое оболочка - F состоит из 14 пар нуклонов, расположенных также квадратом.
Мы приняли, что структура ядра атома отражается в структуре его электронных оболочек. При этом в каждом слое ядра внешними (наружными) будут оболочки, полностью или не полностью достроенные. Так, если внешняя оболочка не достроена, то внешней окажется также часть протонов предыдущей оболочки. К этим протонам, части внешней и части предыдущей оболочки могут быть присоединены дополнительные нейтроны. С этой точки зрения, попробуем представить структуру ядра Урана 238.
Поскольку дополнительные нейтроны могут быть присоединены к атому только с внешней стороны ядра и только к протонам, то нас будет интересовать количество протонов во внешних оболочках по слоям у ядра Урана 238. Электронные слои Урана 238 представлены ниже.
Таблица 5. Электронные оболочки Урана 238.
| 1S | 2S | 2P | 3S | 3P | 3D | 4S | 4P | 4D | 4F | 5S | 5P | 5D | 5F | 6S | 6P | 6D | 7S |
| 2 | 2 | 6 | 2 | 6 | 10 | 2 | 6 | 10 | 14 | 2 | 6 | 10 | 3 | 2 | 6 | 1 | 2 |
Структура ядра будет соответствовать структуре электронных оболочек.
В первом слое ядра наружной будет достроенная S – оболочка - 2 протона;
Во втором слое – достроенная P – оболочка - 6 протонов;
В третьем слое – достроенная D – оболочка – 10 протонов;
В четвертом слое – достроенная F – оболочка – 14 протонов;
В пятом слое наружными будут часть D – оболочки – 7 протонов, и часть – F – оболочки – 3 протона;
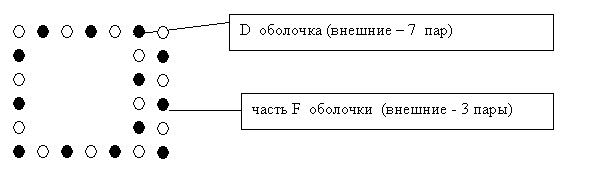
Рисунок 16. Пятый слой
В шестом слое наружными будут часть Р – оболочки – 5 протонов, и часть – D – оболочки – 1 протон;
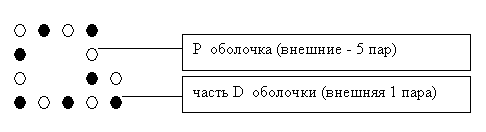
Рисунок 17. Шестой слой
В седьмом слое – S – оболочка - 2 протона; Показывать ее не будем, у нее внешние - 2 пары.
Всего, таким образом, наружными, по слоям, в ядре атома Урана 238 будут 50 протонов, к которым могут быть присоединены лишние нейтроны. Но количество лишних нейтронов, которые он имеет на самом деле 54. Четыре добавочных нейтрона, видимо, присоединены перпендикулярно к наружным первому и седьмому S – слоям. Боковой вид на ядро Урана 238 послойно приведен ниже.
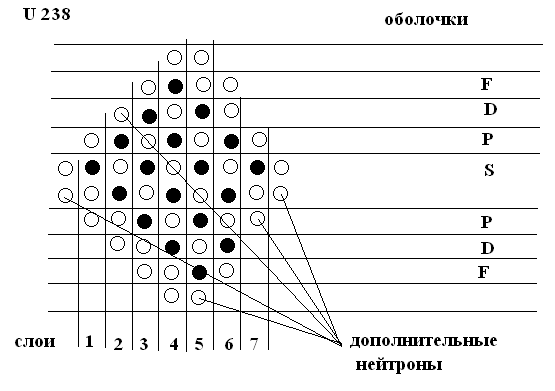
Рисунок 18. Боковой вид на ядро Урана 238 (в разрезе).
На рисунке видна явная несимметричность ядра Урана 238, которая проявляется при радиоактивном распаде в виде его несимметричного деления. Быстрый нейтрон, видимо, делит ядро атома Урана 238 между четвертым и пятым слоями. При этом больший осколок, уменьшает количество нуклонных пар во внешнем четвертом слое до 10, а четырнадцать нуклонных пар 4F слоя, образуют новые пятый и шестой слои. В зависимости от вектора входа свободного нейтрона в ядро, зависит распределение по двум осколкам нуклонов 4F слоя и точное значение протонов и нейтронов в полученных осколках , получаемых при ядерном делении.
На основании сделанного ранее предположения о структуре ядра, можно вывести количественное правило :
Максимальная масса ядра изотопа любого элемента определяется как сумма удвоенного порядкового номера элемента и количества нейтронов, которые могут быть присоединены к внешним протонам в достроенных и недостроенных оболочках ядра по слоям снаружи или сбоку.
Как видно из предложенных рисунков, атомное ядро в результате построения оболочек все больше напоминает куб. Если у ядра не будут появляться оболочки большие чем F оболочка, то полностью достроенный куб, будет иметь следующую структуру:
Таблица 6. Электронные оболочки элемента 120
| 1s | 2s | 2p | 3s | 3p | 3d | 4s | 4p | 4d | 4f | 5s | 5p | 5d | 5f | 6s | 6p | 6d | 7s | 7p | 8s |
| 2 | 2 | 6 | 2 | 6 | 10 | 2 | 6 | 10 | 14 | 2 | 6 | 10 | 14 | 2 | 6 | 10 | 2 | 6 | 2 |
Порядковый номер атома будет – 120, атомный вес 300-308. Скорее всего, атом будет относительно стабилен.
Образование следующих химических элементов будет происходить за счет дальнейшего увеличения массы ядра, что возможно только за счет дополнительной оболочки, которая видимо, будет строиться над оболочкой 5F, и будет состоять из 18 нуклонных пар. Назовем ее оболочкой 5B.
Таблица 7. Электронные оболочки элементов 121-138.
| 1s | 2s | 2p | 3s | 3p | 3d | 4s | 4p | 4d | 4f | 5s | 5p | 5d | 5f | 5b | 6s | 6p | 6d | 7s | 7p | 8s |
| 2 | 2 | 6 | 2 | 6 | 10 | 2 | 6 | 10 | 14 | 2 | 6 | 10 | 14 | 1 -18 | 2 | 6 | 10 | 2 | 6 | 2 |
В таблице на месте оболочки 5b указано 1-18, т.е. количество возможных нуклонных пар. После заполнения оболочки 5b, последует заполнение оболочек 6f, 7d, 8p, 9s, 6 b… и так далее по подобию.
Предложенная модель ядра атома прекрасно объясняет наличие “магических” чисел протонов и нейтронов. (2, 8, 20, 28, 50, 82, ...) Также предложенная модель объясняет возникновение “ротационного спектра” (т.е. факта вращения ядра как целого), необъяснимому в рамках “полевой” или квантовой теории. И безусловно, наглядно видна несферичность ядер в ротационной модели, предложенной Дж.Рейнуотером еще в 1950 г.
ЗАКЛЮЧЕНИЕ
Безусловно, все вышеприведенное противоречит общепринятым сегодня теориям, которые рассматривают частицы как возбужденное состояние некоего поля.
Но стоит напомнить, что “полевое” представление частиц просто всего лишь очень удобная форма математического приблизительного описания процессов и взаимодействия самих частиц и ничто иное. В данном случае математика, игнорируя свою вспомогательную роль, начинает подавлять и подменять собой саму физику.
Никто и никогда не отменял доказанную опытом пространственную структуру элементарных частиц и их размеры. А там, где есть размеры – есть трехмерный объем.
Аргумент о “противоречии” сложившимся представлениям, можно было бы принять, если бы на протяжении жизни даже одного поколения, эти представления в физике элементарных частиц не менялись бы так часто, и то, что вчера казалось абстрактным бредом, не получало бы всеобщего признания и не становилось очередной “Библией” для физиков.
Автор полагает, что геометрическая теория нуждается в дальнейшем развитии и что с ее помощью можно будет лучше понять устройство нашего мира.
29-04-2015, 05:12
