ХАОС, НЕОБРАТИМОСТЬ ВРЕМЕНИ И БРЮССЕЛЬСКАЯ ИНТЕРПРЕТАЦИЯ КВАНТОВОЙ МЕХАНИКИ. КОНЦЕПЦИЯ И.ПРИГОЖИНА
Содержание
0. ВВЕДЕНИЕ
1. ХАОС
1.1 Классический динамический хаос: неустойчивость по начальным условиям
1.2 Классический хаос: неинтегрируемые системы Пуанкаре
1.3 Статистическое описание. Диссипативный хаос
2. НЕОБРАТИМОСТЬ ВРЕМЕНИ
2.1 Обратимость времени в классической и квантовой механике
2.2 Роль необратимости в статистической механике. Потоки корреляций
2.3 Проблема несводимого описания
3. БРЮССЕЛЬСКАЯ ИНТЕРПРЕТАЦИЯ КВАНТОВОЙ МЕХАНИКИ
3.1 Альтернативные интерпретации квантовой механики
3.2 Неунитарная эволюция и несводимое описание
4. ЗАКЛЮЧЕНИЕ
СПИСОК ЛИТЕРАТУРЫ
0. ВВЕДЕНИЕ
Начиная с времён Галилея и Ньютона современная физика проделала огромный путь по накоплению, систематизации, описанию и осмыслению фактов об окружающем мире. Описание обычно делалось на языке математики, и сама структура этого языка зачастую позволяла совершать новые открытия в реальном мире (что само по себе достаточно удивительно). За несколько столетий предсказательная роль физики стала настолько большой, что в настоящее время нерешаемых "счётных" задач практически не осталось – по крайней мере, с точки зрения принципиального понимания происходящих явлений – ни в механике, ни в классической электродинамике, ни в квантовой теории.
Физика продолжает развиваться, и за последние десятилетия возрос интерес к таким её новым областям, как синергетика, динамический хаос и самоорганизация. В этих ветвях физики зачастую используется оригинальный математический аппарат, а в сочетании с возрастающей мощностью компьютеров и возможностей "численного эксперимента" предсказательная сила их оказывается вполне "на уровне", наряду с традиционными физическими теориями.
В то же время возникли некоторые проблемы, лежащие скорее в области не математики, а философии физики. Различные физические теории – старые и новые – "не стыкуются" друг с другом в отношении определённых фундаментальных понятий и явлений – в частности, детерминизма и необратимости времени.
На макроскопическом уровне необратимость времени входит не только в "новую физику", но, например, и в разработанную в прошлом веке термодинамику. Трудности возникают при перекидывании моста с классических механических моделей, основанных на обратимых во времени гамильтоновых уравнениях, к явно диссипативному, необратимому, поведению реальных физических систем и теориям, их описывающим. Это один пример.
Другой пример физической проблемы философского плана – возникновение хаотического поведения у простых систем, описываемых детерминистскими уравнениями движения. И вновь – существующие теории хаоса вполне эффективно работают и описывают такие системы, но "моста" к классической части физики нет. Откуда берётся хаос в детерминированных системах?
Данная работа посвящена взглядам на эти вопросы, развиваемым так называемой "брюссельской школой", идейным руководителем которой является известный биофизик, синергетик, лауреат Нобелевской премии по химии за 1977 г. Илья Пригожин.
Основная особенность научной концепции, развиваемой И.Пригожиным – необратимость времени на микроскопическом уровне. Не отрицая ни законов, ни результатов традиционной физики, Пригожин предлагает новую интерпретацию этих результатов. Технически это выражается как поиск решений всё тех же уравнений (уравнений Гамильтона, Лиувилля, Шрёдингера и т.д.) – но в новом классе функций, в новом функциональном пространстве.
В разделе 1 настоящей работы рассматриваются примеры классического динамического хаоса в простейших математических моделях сдвига Бернулли и преобразования пекаря (неустойчивость по начальным условиям), а также фундаментальное свойство неинтегрируемости многих динамических систем (теорема Пуанкаре), также приводящее к хаотическому поведению.
Раздел 2 посвящён проблемам сводимости "макроскопического" хаоса к "микроскопическому" и проблеме обратимости времени. Существенно, что и в классической механике, и в копенгагенской интерпретации квантовой механики описание необратимого поведения макроскопических систем исходя из обратимых микроскопических законов наталкивается на существенные трудности.
В разделе 3 вкратце описаны основные интерпретации квантовой механики: копенгагенская, статистическая, многомировая интерпретация Эверетта. Основное же внимание уделяется брюссельской интерпретации квантовой механики, развиваемой И.Пригожиным. Особенности её математического аппарата поясняются на простых примерах динамических систем, уже рассмотренных в предыдущих разделах. Общая концепция неунитарной эволюции приводит к тому, что единственно адекватным становится статистическое описание систем – как классических, так и квантовых. Для случая последних проясняются некоторые известные парадоксы известных интерпретаций квантовой механики, связанные с ролью внешнего наблюдателя.
К сожалению, идеи И.Пригожина требуют для своего изложения (даже в популярном виде) существенного использования математического аппарата, что привело к некоторой перегруженности текста формулами. Автор, однако, надеется, что "лес" за "деревьями" не скрылся, и основные положения физической концепции Брюссельской школы нашли отражение в настоящей работе.
1. ХАОС
Их либе жизнь и обожаю хаос...
И.Бродский, "Два часа в резервуаре"
1.1 Классический динамический хаос: неустойчивость по начальным условиям
Хаотическое поведение может возникать даже в очень простых системах, например, из физических моделей – в колебаниях сферического маятника с двумя степенями свободы. Мы для начала рассмотрим даже ещё более простые математические модели с дискретным временем – сдвиг Бернулли и преобразование пекаря.
Сдвиг Бернулли представляет собой отображение в одномерном пространстве на интервале (0,1) по закону
xn+1 =2xn (mod1).
Это уравнение движения детерминистично: по заданному xn однозначно вычисляется xn+1 . При этом, однако, сдвиг Бернулли не является обратимым отображением. Симметрия во времени нарушена ещё на уровне уравнения движения. Этим сдвиг Бернулли отличается от динамических систем с обратимыми уравнениями движения.
Сдвиг Бернулли представляет собой пример детерминистического хаоса. Можно представить примеры последовательностей, начинающихся с какого-нибудь произвольного числа, например:
{0.13; 0.26; 0.52; 0.04; 0.08; 0.16; 0.32; 0.64; 0.28... }
и
{0.14; 0.28; 0.56; 0.12; 0.24; 0.48; 0.96; 0.92; 0.84... } –
как видим, незначительное отличие в начальных условиях уже на 4-м шаге порождает существенное различие траекторий, а в дальнейшем их поведение совершенно различно.
Легко показать, что со временем разойдутся траектории любых двух сколь угодно близких точек. Запишем число x в виде двоичной дроби:
x=0.u–1 u–2 u–3 ...u–k ...=u–1 /2 + u–2 /22 + u–3 /23 + ... + u–k /2k + ...
Описанное выше отображение соответствует сдвигу u–k '=u–(k+1) , откуда становится понятным название "сдвиг Бернулли". Видно, что нулевой разряд числа при этом теряется, что соответствует не-взаимооднозначности отображения.
Описание эволюции динамической системы типа сдвига Бернулли в терминах траектории неадекватно, так как для адекватности траектория должна оставаться "почти одной и той же" при незначительном изменении начальных условий.
В данном же случае имеет смысл обратиться к статистическому описанию, введя плотность вероятности r (x) пребывания системы в каждой точке x интервала (0,1) . Отображение представляет собой оператор U , действующий на эту функцию:
r n+1 =U r n (x)= ( r n (x/2)+ r n ((x+1)/2) ) / 2.
Оказывается, что при многократном применении оператора отображения к произвольному распределению плотности вероятности оно стремится к константе:
r n =Un r 0 (x) ® r µ (x)=const.
В дальнейшем мы ещё вернемся к отображению Бернулли и свойствам его оператора, а пока рассмотрим другую простую динамическую систему, теперь уже двумерную, называемую преобразованием пекаря:
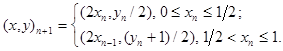
Правило, определяющее преобразование пекаря, очень просто. Сначала квадрат со стороной, равной 1, сплющивается в прямоугольник длиной 2 и высотой 1/2 , затем правая половина полученного прямоугольника накладывается на левую, образуя новый квадрат. Процесс в чём-то аналогичен размешиванию теста, отсюда и название.
В отличие от сдвига Бернулли преобразование пекаря обратимо во времени. Однако оно точно так же порождает хаотическое движение, связанное с неустойчивостью по начальным условиям.
Преобразование пекаря сводится к сдвигу в двусторонней двоичной последовательности:
x0y = ....u–k... u–3 u-2 u–1 u0 u1 u2 ...uk ....,
uk ' = u–(k+1) .
Видно, что при этом никакие двоичные разряды не теряются, что и соответствует обратимости преобразования пекаря во времени.
Аналогично сдвигу Бернулли, преобразование пекаря порождает динамический хаос, и описание движения точки в терминах траекторий также неадекватно.
В случае преобразования пекаря описание эволюции системы в статистических терминах даже более "физически осмысленно", чем для сдвига Бернулли. Дело в том, что теперь, в двумерном случае, можно рассматривать координатную плоскость как фазовое пространство некоторой динамической системы с одной степенью свободы: ось x соответствует координате, а ось y – импульсу. Аналогия с "физическими" динамическими системами усиливается ещё и тем, что выполняется теорема Лиувилля: сохраняется объём в фазовом пространстве. Другими словами, взяв ансамбль точек внутри некоторой области и проделав произвольное количество преобразований пекаря, мы обнаружим тоже самое количество точек внутри некоторой другой области (форма её при этом очень сильно изменится и станет крайне замысловатой). Объём этой области (в нашем двумерном случае ему соответствует площадь) останется неизменным.
Несмотря на обратимость преобразования пекаря во времени, эволюция при t ® + µ и при t ® – µ оказывается различной [1,c.114].
Кроме описанных выше, существует ещё много сравнительно простых моделей динамического хаоса. Однако мы воздержимся от их подробного рассмотрения, и перейдём теперь к причинам, лежащим в основе непредсказуемого поведения физических систем.
1.2 Классический хаос: неинтегрируемые системы Пуанкаре
Чем простое отличается от сложного? Традиционный ответ содержит ссылку на иерархию. На одном конце шкалы мы находим такие объекты, как маятник, подчиняющийся простым детерминистским законам. На другом конце шкалы находятся люди и их сообщества. Между этими полюсами можно мысленно вписать целую иерархию "комплексификации" – возникновения сложного из простого. В действительности же дело обстоит даже более тонко: простое и сложное могут сосуществовать вместе, не будучи связаны между собой иерархически.
Что касается человеческих сообществ, теория их поведения крайне трудно поддаётся хоть какой-нибудь математизации и заслуживает отдельного рассмотрения, вне рамок настоящей работы. Пример же хаотического поведения простейших физических систем типа маятника будет рассмотрен ниже.
При исследовании того, как простое относится к сложному, обычно широко используется понятие аттрактора, то есть конечного состояния или хода эволюции диссипативной системы. Смысл этого понятия был глубоко преобразован современной физикой и математикой. В прошлом считалось, что все системы, эволюция которых связана с существованием аттрактора, одинаковы. Ныне понятие аттрактора связывают с разнообразием диссипативных систем.
Идеальный маятник без трения не имеет аттрактора и колеблется бесконечно. С другой стороны, движение реального маятника – диссипативной системы, движение которой включает трение, – постепенно останавливается в положении равновесия. Это положение является аттрактором. Аналогичным образом, аттрактором является и состояние термодинамического равновесия: ансамбль из миллиардов и миллиардов частиц, образующих изолированную систему, эволюционирует к состоянию равновесия, описание которого зависит лишь от немногих параметров, таких как температура и давление.
Идеальный маятник служит примером так называемой структурной неустойчивости: в отсутствие трения аттрактор не существует, но введение даже самого незначительного трения изменяет движение маятника и вводит аттрактор.
Чтобы представить аттрактор геометрически, обычно вводят пространство, размерность которого совпадает с числом переменных, необходимых для описания системы. Это могут быть координаты, импульсы, различные термодинамические переменные. Во введённом пространстве равновесное состояние диссипативных систем соответствует точечному аттрактору. То же относится и к стационарным состояниям систем, близких к термодинамическому равновесию и удовлетворяющим теореме о минимальном производстве энтропии. Во всех случаях, каково бы ни было первоначальное приготовление системы, её эволюция может быть описана траекторией, ведущей из точки, которая представляет начальное состояние, к аттрактору. Таким образом, конечная точка – аттрактор – представляет собой финальное состояние всех траекторий.
Не все диссипативные системы приводят к одной-единственной конечной точке. Например, сильно неравновесная диссипативная структура, известная под названием "химические часы", эволюционирует не к какому-нибудь состоянию, а к устойчивому периодическому режиму. Такая ситуация приводит к необходимости обобщения идеи аттрактора: аттрактор более не точка, а линия, описывающая периодическое во времени изменение концентрации химических веществ. Примеры подобных аттракторов легко найти, например, и в радиофизике – ими являются предельные циклы автогенераторов, – и во многих других разделах естествознания.
Система с предельным циклом остаётся предсказуемой и потому допускает простое описание. Но за этой простотой кроются неожиданные свойства. Нетрудно представить себе химическое равновесие – множество химических процессов, компенсирующих друг друга подобно тому, как в состоянии демографического равновесия рождаемость компенсирует смертность. Но воображение бессильно представить себе, как огромные количества молекул, взаимодействующих только через столкновения, начинают вдруг действовать "дружно" – так, что среда периодически изменяет свой цвет.
В других случаях, пытаясь построить изображение аттрактора, мы получим не точку или замкнутую линию, а поверхность или объём. Поворотным же событием стало открытие аттракторов, не относящихся к столь простым геометрическим объектам – так называемым странных аттракторов. В отличие от линии или поверхности, странные аттракторы представляют собой фрактальные объекты, характеризующиеся дробной размерностью.
Странные аттракторы были обнаружены в поведении многих динамических систем, описываемых детерминистическими уравнениями движения. Например, они возникают для так называемого сферического маятника – обыкновенного грузика на нитке, который совершает колебания не в плоскости, а по поверхности полусферы. При внесении возмущений в виде колебаний точки подвеса в некоторый критический момент (зависящий от частоты возмущения) движение маятника становится хаотическим, а его траектория описывается странным аттрактором [1, с.83].
Корреляционный анализ временны'х последовательностей, характеризующих работу человеческого мозга, изменения климата на планете за миллионы лет и курса акций на бирже также приводит к обнаружению странных аттракторов. Впрочем, при наличии огромного количества внешних причин, влияющих на поведение всех этих систем, случайность их поведения вроде бы удивления не вызывает, поэтому пока обратим внимание на более загадочное явление. Откуда возникает хаотическое поведение в случае сферического маятника?
Как было показано выше, хаотическое поведение отображений типа сдвига Бернулли связано с неустойчивостью по начальным условиям, а необратимость их во времени – с потерей информации при сдвиге двоичной записи числа. Можно, однако, возразить, что приведённые примеры отображений несколько искусственны, так как в природе не встречается подобных дискретных процессов, да и "вычислительной мощности" природы не хватит на выполнение столь мудрёной операций, как модульная арифметика.
Оказывается, однако, что и на уровне решения обычных уравнений движений (вытекающих из законов Ньютона) для того же маятника возможно получение неустойчивых решений, связанных с так называемой неинтегрируемостью системы по Пуанкаре.
Основная проблема классической механики состоит в расчёте движения взаимодействующих тел на основе их уравнений движения (в частном случае, например, это может быть закон Ньютона F =ma ). Обобщение ньютоновской механики на более сложные системы показало, что более удобной формой описания является не зависимость от времени пространственной траектории системы (в нашем примере – координаты), а движение точки, изображающей систему, в пространстве вдвое большей размерности, чем обычное "физическое". В общем случае состояние динамической системы описывается координатами q1 , ..., qs , которые являются независимыми переменными, и соответствующими им импульсами p1 , ..., ps . Преимуществом такого подхода является существенное упрощение уравнений движения.
Центральная величина всей гамильтоновой механики – функция Гамильтона, или гамильтониан – это, в простейшем случае, выраженная через координаты и импульсы
энергия системы (Строгое изложение гамильтоновой механики – см. [3]). В гамильтоновском описании число независимых переменных удваивается, но уравнения движения существенно упрощаются. Рассмотрим систему N
точек. Каждой из 3N
координат N
точек соответствует каноническое уравнение движения 
. Аналогично, каждому из 3N импульсов соответствует каноническое уравнение движения вида 
. В качестве частного случая рассмотрим свободные, то есть невзаимодействующие, частицы. Гамильтониан для них зависит только от импульсов (потенциальной энергии нет). Тогда из канонических уравнений следует, что импульсы постоянны во времени (
), и что координаты, задающие положение частиц, – линейные функции времени. Этот тривиальный случай играет, тем не менее, весьма важную роль в общей проблеме интегрирования гамильтоновых уравнений движения.
Чтобы ввести понятие интегрируемой системы, обратимся к другому простому примеру – маятнику на пружинке, одномерному гармоническому осциллятору. Гамильтониан для него имеет вид 
, где k
– жёсткость пружины, q
– смещение груза от положения равновесия. Чтобы упростить уравнения движения, введём новые переменные a
и J
вместо старых q
и p
:
,
,
где 
– собственная частота колебаний осциллятора. Переменная a
называется угловой переменной, J
– переменной действия. В переменных угол–действие гамильтониан принимает простой вид: H=
w
J
. Он теперь зависит только от нового импульса – переменной действия. В результате, как и в случае свободных частиц, 
, то есть переменная действия является инвариантом движения. Что же касается угловой переменной, то 
, она меняется линейно по времени.
Переход от переменных p, q к переменным J, a называется каноническим преобразованием . В данном случае оно позволило исключить из гамильтониана член, ответственный за потенциальную энергию. Аналогичное преобразование можно иногда проделать и в случае системы со многими степенями свободы, исключив из гамильтониана межчастичное взаимодействие, и выразить движение в циклических переменных . Их название относится к периодическому характеру движения, который делается явным в таких переменных.
Особую важную роль играют частоты системыw 1 , w 2 , ..., w n . Именно через эти частоты мы приходим к понятию резонанса, имеющего решающее значение для теоремы Пуанкаре.
Движение интегрируемой системы с двумя степенями свободы можно представить на торе. Возможны две ситуации. Если для некоторых целых n1
и n2
выполняется условие n1
w
1
+ n2
w
2
=0
, то есть частоты соизмеримы, мы имеем резонанс, и движение на торе периодическое – траектория замкнутая. Если же эта сумма ни при каких комбинациях n1
и n2
не равна нулю, то траектория навивается на поверхность тора и никогда не замыкается. В конце концов, как показано Пуанкаре, такая траектория проходит сколь угодно близко к произвольной точке на поверхности тора. Траектория при этом
29-04-2015, 01:58