Гидравлический прыжок

Определяем удельный фильтрационный расход по формуле :

, ( 4.5 )

где - значение отношения удельного расхода и коэффициента фильтрации , взятого из графиков на рис.4.1 .

Схема плотины представлена на рис. 4.2 .

Для построения кривой депрессии воспользуемся следующей формулой :

( 4.6 )

Для глубин используются пределы :

Для рассматриваемых участков длины используем пределы :

Результаты расчетов по формуле ( 4.6 ) сведены в нижеследующую таблицу :

Таблица 3.2.

	5	10	15	20	25	30	35	40	45.4
	10.5	12.2	13.6	15.0	16.2	17.3	18.4	19.4	20.4

По данным таблицы 4.2 строим кривую депрессии ( смотри рис.4.3. ) .

3.2. Расчет плотины с ядром и дренажным банкетом .

Для определения удельного фильтрационного расхода и построения кривой депрессии заменяем данную плотину на однородную . Вычисляем длину виртуальную , заменяющую ядро :

, ( 4.7 )

где - толщина ядра , ;- коэффициент фильтрации ядра , .

Для нашего случая :

Виртуальная длина прямоугольника , заменяющего плотину определяется по формуле :

( 4.8 )

Для нашего случая :

Для построения кривой депрессии будем задаваться горизонтальными величинами , вычисляя глубину по формуле :

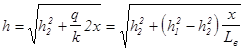( 4.9 )

Вычисления , выполненные по этой формуле , сведены в таблицу :

Таблица 4.3.

	5	10	15	20	25	30	60	90	100	105	110	115	121.2
	6.1	7.3	8.4	9.3	10.1	10.9	14.7	17.7	18.6	19.1	19.5	19.9	20.4

По данным таблицы 4.3. строим кривую депрессии ( смотри рис.4.4 ) .

Удельный фильтрационный расход определяем по формуле :

( 4.10 )

, м

, м

, м

, м

, м

, м

, м

4. Расчет фильтрации воды под бетонной водосливной плотиной .

4.1. Расчет методом коэффициентов сопротивления .

Пользуясь вышеуказанным методом нужно решить три задачи :

1. построить эпюру противодавления , найти величину и точку приложения силы противодавления ;

2. найти максимальную скорость фильтрации на поверхности дна нижнего бьефа ;

3. определить величину удельного фильтрационного расхода .

При решении вышеперечисленных задач задаемся определенным размером фиктивной эквивалентной трубы, т.е. размером , причем эта величина будет различной для указанных выше трех фильтрационных задач .

Далее через ,, будем обозначать заглубления расчетного водоупора , принимаемые соответственно при решении 1-й , 2-й и 3-й задачи.

1. Определение силы противодавления .

Для построения эпюры противодавления величину принимаем равной :

, ( 5.1 )

где - активная зона фильтрации по напору , м ;- длина проекции подземного контура на вертикаль , S0=

( - параметры плотины в м ) ; - длина проекции подземного контура на горизонталь , ( - параметры плотины в м ) .

В нашем случае используется формула ( 5.1 ) , т. к. отношение параметров подземного контура , что лежит в пределах .

Заданный подземный контур разбиваем на отдельные элементы . Вдоль каждого из них теряется напор , который рассчитывается по формуле :

, ( 5.2 )

где - перепад на сооружении , ( - горизонт воды верхнего бьефа , - горизонт воды нижнего бьефа ) ;- коэффициент сопротивления i-ого элемента подземного контура ; - cуммарный коэффициент сопротивления всего подземного контура .

Находим коэффициенты сопротивления :

1). входного элемента подземного контура

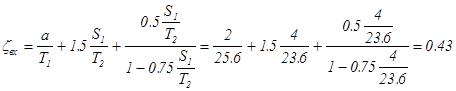
2). выходного элемента подземного контура

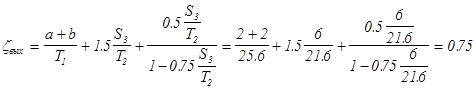
3). внутреннего шпунта

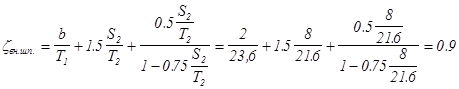
4). первого горизонтального элемента подземного контура

5). второго горизонтального элемента подземного контура

По формуле ( 5.2 ) рассчитываем потери напора на элементах подземного контура :

1). входного элемента подземного контура

2). выходного элемента подземного контура

3). внутреннего шпунта

4). первого горизонтального элемента подземного контура

5). второго горизонтального элемента подземного контура

Строим по вычисленным потерям напора пьезометрическую линию ( смотри рис. 5.1 ) и получаем искомую эпюру противодавления ( смотри площадь , заштрихованную на рис. 5.1 ) .

Сила противодавления ищется по следующей формуле :

, ( 5.3 )

где - ширина плотины ( принимаем ) ; - удельный вес воды () ; - площадь эпюры противодавления , в м2 (,- площади эпюр противодавления на разных участках подземного контура ) .

Площади эпюр противодавления на разных участках подземного контура ищутся как площади трапеций :

Площадь полной эпюры противодавления равна :

Сила противодавления ищется по формуле ( 5.3 ) :

Определение максимальной скорости фильтрации .

Для определения максимальной скорости фильтрации принимаем величину равной :

, ( 5.4 )

где - действительная зона фильтрации .

В нашем случае используется формула ( 5.4 ) , т. к. .

Для определения максимальной скорости фильтрации рассчитываем коэффициенты сопротивления так же , как и при решении предедущей задачи .

Находим коэффициенты сопротивления :

1). входного элемента подземного контура

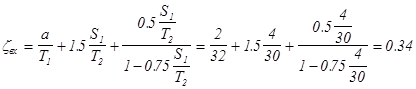
2). выходного элемента подземного контура

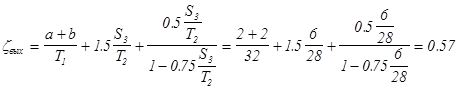
3). внутреннего шпунта

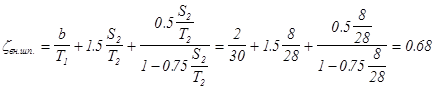
4). первого горизонтального элемента подземного контура

5). второго горизонтального элемента подземного контура

Максимальная скорость фильтрации рассчитывается по формуле :

, ( 5.5 )

где _ - коэффициент фильтрации ,;- максимальный выходной градиент .

Максимальный выходной градиент определяется по формуле :

, ( 5.6 )

где параметр рассчитывается по следующей формуле :

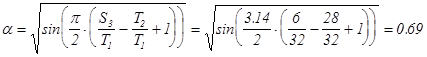( 5.7 )

Вышеуказанные величины будут равны :

3. Определение удельного фильтрационного расхода .

Для определения удельного фильтрационного расхода принимаем величину равной :

Для определения удельного фильтрационного расхода коэффициенты сопротивления берутся такие же , как и в предедущей задаче .

Удельный фильтрационный расход определяем по формуле :

4.2. Расчет при помощи экспериментального метода электродинамических аналогий (метода ЭГДА ).

1. Нахождене фильтрационного расхода.

Рассматриваем область грунта , заключенную между двумя соседними линиями равного напора ( смотри рис. 5.2 ) и .

Пример расчета для отсека грунта №1 :

а). длина отсека грунта - ;

б). ширина отсека грунта - ;

в). средний пьезометрический уклон ищется по следующей формуле -

; ( 5.8 )

г). скорость фильтрации определяем по формуле ( 5.5 ) :

д). фильтрационный расход ищется по формуле -

( 5.9 )

2. Определение скоростей фильтрации на поверхности дна нижнего бьефа .

На поверхности дна нижнего бьефа отметим четыре точки , для которых будем определять скорости фильрации . Ниже приведен пример расчета для точки №1 :

а). расстояние между соседними линиями равного напора вдоль линии дна нижнего бьефа ;

б). средний пьезометрический уклон ищется по формуле ( 5.8 ) :

в). скорость фильтрации определяем по формуле ( 5.5 ) :

По полученным значениям скоростей строится эпюра выходных скоростей (смотри рис.5.2 ) .

Определение противодавления , действующего на подошву плотины .

На подошве плотины намечаем девять характкрных точек ирассматриваем величину противодавления в них.

Ниже приведе пример расчета для первой точки :

а). заглубление точки ;

б). напор в точке ;

в). пьезометрическая высота определяется из уравнения -

, ( 5.10 )

где - координата точки относительно плоскости сравнения , м .

По полученным данным строим эпюру изменения напора и давления вдоль подземного контура , а также эпюру давления , действующего на горизонтальные элементы подземного контура ( смотри рис. 5.3 ).

Величину гидродинамического давления находим по формуле :

Список литературы

1. Чугаев Р.Р. Гидравлика ( техническая механика жидкости ) . - Л.: Энергоиздат , 1982. - 672 с.

2. Кожевникова Е.Н. , Орлов В.Т. Методические указания по выполнению курсовых и расчетно-грвфических работ по курсу гидравлики . - Л. : Издание ЛПИ им. М.И. Калинина , 1985. - 48 с.