.
При этом 
означает: 
.
В СО1 после переноса тела 2:
,
Поскольку , 
, то, следовательно,
.
Поэтому переход от ИСО к СО1 равнозначен переносу в эту СО1 тела 2, сопровождающемуся суммированием масс 
, а также переносу в СО1 самой ИСО.
И обратно, переход от СО1 к ИСО равнозначен выделению из тела 1, находящегося в СО1, некоторого тела 2 с массой 
.
После переноса тела 2 в СО1 совместная масса тел, находящихся в СО1: 
.
Итак, для тела, находящегося в СО1, масса тела может быть найдена измерениями в самой СО1, при использовании в процессе измерений тела бесконечно малой (не возмущающей) массы 
(пробного тела).
Взаимодействие тел с существенно различными массами
В частном случае взаимодействия масса тела 2 может быть много меньше массы тела 1: 
, что означает: 
или 
.
Выполним переход от ИСО к СО1 для данного случая.
В ИСО до перехода к СО1 (переноса тела 2 в СО1):
, 
,
, 
,,.
В СО1 до переноса тела 2:
,
.
Ввиду малости 
относительно 
имеем:
,
.
В ИСО после перехода к СО1, соответствующего переносу в СО1 тела 2 с массой 
: 
, 
,
, 
.
Ввиду малости относительно 
и относительно , имеем: 
,,,
.
В СО1 после переноса в нее тела 2:
, 
,
т.е. присоединение тела 2 малой массы 
к телу 1 большой массы не изменяет массу тела 1 и ускорение 
, приобретаемое телом бесконечно малой массы относительно СО1.
Эксперимент Галилея
Именно такой случай обнаружен в эксперименте Галилея, “опровергнувшим” тезис Аристотеля о неравенстве ускорений тел, обладающих различными массами.
Эксперимент, выполненный в СО1, где тело 1 - Земля (объект с очень большой массой ), тело 2 - любой объект с малой массой , показал, что в пределах точности измерений ускорение тела 2 не зависит от массы .
В самом деле, при 
присоединение массы к массе , задающее переход от ИСО к СО1, ввиду малости практически не изменяет , т.е. ускорение 
, приобретаемое “галилеевским” пробным телом пренебрежимо малой массы относительно тела большой массы действительно не зависит от .
Итак, результат Галилея относится к частному случаю взаимодействия тел с существенно неравными массами.
Он устанавливает фактически способ определения СО1 в качестве местной ИСО относительно некоторых, вполне определенных для данной СО1 и данной точности измерений галилеевских объектов с помощью самих этих объектов.
Его заключение таково: “Данный эксперимент устанавливает, что для данных галилеевских объектов данное небесное тело является телом достаточно большой массы , чтобы его СО1 для данных галилеевских объектов и при данной точности измерений могла быть принята в качестве местной ИСО”.
Для тела 1 с малой массой или тела 2 с большой массой он бы получил другой результат, чтобы констатировать в свою очередь: “Эксперимент устанавливает, что для данных объектов данная СО1 с точностью, определяемой точностью измерений, не может считаться местной ИСО” или иначе: “Данные объекты относительно ИСО = СО1 с точностью, определяемой точностью измерений, не могут считаться галилеевскими объектами, имеющими бесконечно малую массу относительно ”.
Посмотрим теперь, как выглядит эксперимент Галилея в общем случае, вначале для произвольной массы , затем для произвольной массы .
Определим предварительно требуемые условия проведения эксперимента.
Пусть мы желаем наблюдать падение тела 2' большой массы в два раза быстрее падения тела 2" галилеевской массы.
Это значит, что за время прохождения телом 2' пути 
(где - высота Пизанской башни) тело 2" проходит путь 
.
Поэтому в СО1, где тело 1 - Земля (объект много большей массы ) тела 2' и 2" имеют разные ускорения 
, 
, причем 
.
Поскольку ускорение любого тела 2 в СО1 равно:
,
то имеем: для галилеевского объекта 
, 
.
Для искомого объекта большой массы :
.
Но 
.
Следовательно 
, 
, т.е. 
.
Таким образом выясняется, что искомый объект 2' большой массы 
и одинаковой геометрии с галилеевским объектом должен иметь массу , равную массе Земли (очевидно при этом, что бросать объекты 2' и 2" можно только поочередно, а после броска тела 2' убирать его куда-нибудь подальше, скажем, за орбиту Луны).
Поэтому полученное Галилеем равенство ускорений есть всего лишь результат “удачно” выбранных галилеевских объектов.
Оценим порядок величин, которые пытался обнаружить Галилей.
Пусть 
, 
.
Опережение 
телом 2' тела 2" в СО1 составляет:
,
где 
, 
, т.е. 
.
При 
с,
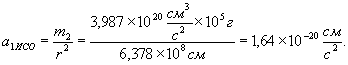
Откуда 
.
Если теперь выбрать в качестве тела 1 тело пренебрежимо малой массы 
, то при измерениях в СО1 галилеевский объект массой 
действительно обладает в 2 раза большим ускорением 
, в полном соответствии с “опровергаемым” положением Аристотеля.
Для этого достаточно обеспечить при массе дробинки 
г и ядра 
кг массу Земли, вместе с находящейся на ней Пизанской башней и экспериментатором-физиком, равную, скажем, 
г.
При этом, однако, возникает новая трудность: при и 
имеем: 
.
При таком ускорении 
путь 
м будет пройден за время 
, равное:
,
т.е. воображаемый Галилей не доживет до конца эксперимента, а за время жизни реального Галилея 
пройденная высота Пизанской башни составит:
так что требуемая точность измерений все еще будет составлять порядка 
.
Если считать, что такая точность измерений не достижима на практике, то тем более недостижима точность измерения по программе “Галилей” за время наблюдения 
c, равное времени наблюдения реального Галилея:
.
При этом экспериментатор рискует вновь прийти к неверному выводу: “ускорение тел не зависит от их массы” и даже в усугубленном виде “перемещения тел не зависят от массы”.
Итак, положение Аристотеля относится к другому частному случаю обратного соотношения масс при измерениях в СО1.
Фактически результат Аристотеля реализуется в самом эксперименте Галилея при переходе от СО1 к СО2, образующем своего рода “инверсию” точки зрения.
Таким образом, оба положения: Аристотеля – “ускорение тела пропорционально массе тела” и Галилея – “ускорение тела не зависит от массы тела” действительно относятся к одному и тому же частному случаю взаимодействия тел 1, 2 с существенно неравными массами.
При этом, однако, для результат Галилея реализуется в СО1, а результат Аристотеля - в СО2.
Оба “взаимоисключающие” положения оказываются верными, относятся к одному и тому же частному случаю взаимодействия и “подтверждаются” одним и тем же экспериментом, но только лишь в разных СО.
В общем же случае верным является положение Ньютона: “В ИСО, для данной пары 1, 2, ускорение объекта 2 не зависит от его массы ”.
Случай Ньютона
Пусть теперь оба тела 1 и 2 имеют не галилеевские большие массы.
Назовем их ньютоновскими объектами 
,
:
,
,
где 
.
Пусть попрежнему 
, а 
.
Тогда поскольку , справедливо: .
С учетом: 
, 
, поскольку 
, при некоторых 
оба ускорения 
, 
, все время оставаясь при этом .
При некотором порядке малости, определяемом заданной точностью измерений, оба ускорения достигают значений, принимаемых за нулевые, причем достигает этого значения много раньше :
, , , .
Поскольку при этом , то ИСО таким образом вновь совмещается с СО1. Другими словами при взаимодействии тел с ньютоновскими массами 
начиная с некоторого минимального (назовем его минимальным ньютоновским расстоянием 
) ИСО вновь, как и в случае галилеевского объекта 
приводится к СО1.
Итак, при взаимодействии ньютоновского и галилеевского объектов 
:
, 
,
, 
, , , 
,
при любом 
.
При взаимодействии двух ньютоновских объектов 
,
с существенно неравными массами 
:
, 
, , 
, 
, 
, 
,
т.е. не при любом, а лишь начиная с некоторого ньютоновского расстояния , определяемого заданной точностью вычислений.
Определим теперь как функцию от заданного соотношения масс , и заданной точности вычислений.
Пусть , 
.
В ИСО ускорения тел 1, 2 составляют:
,
.
Видно, что 
и отличаются от и только на величину , т.е. сама СО1 отличается от ИСО в пределах 
.
Если теперь (ввиду ), то при определенной точности вычислений ею можно пренебречь, т.е. принять: , 
.
При этом: 
, где 
- погрешность приближения, вносимая заменой истинной ИСО приближенной 
.
Поскольку 
, имеем: 
.
Откуда минимальное ньютоновское расстояние , соответствующее допускаемой максимальной погрешности приближения , составляет: 
.
Например, в ньютоновской системе 1, 2, где тело 1 - Земля, 
, тело 2 - Луна, 
, 
, имеем:
,
.
Примем теперь СО1 в качестве приближенной ИСО.
Получим: , 
.
При этом погрешность приближения составляет:
.
При заданной погрешности приближения, например, 
имеем:
.
Поскольку реальное удовлетворяет заданной погрешности приближения, принятие СО1 в качестве приближенной ИСО в данном случае допустимо.
При меньшем допускаемом значении погрешности приближения, например, 
минимальное ньютоновское расстояние для данной пары 1, 2 ньютоновских объектов составляет уже 
, что не обеспечивается в реальной паре, т.е. в данном случае принятие СО1 в качестве приближенной ИСО не допустимо.
Ньютоновский вопрос, обычно выражаемый примерно так: “Является ли сила, действующая на расстоянии до Луны, силой того же рода, что и на поверхности Земли” или, в несколько уточненной формулировке: “Является ли сила, действующая на ньютоновский “большой” объект, находящийся на расстоянии до Луны, силой того же рода, что и действующая на галилеевский “малый” объект, находящийся, вообще говоря, на любом расстоянии, в том числе и на расстоянии до Луны”, в форме наиболее отвечающей сути поисков Ньютона, может выглядеть еще и так: “Является ли ИСО двух ньютоновских “больших” объектов, находящихся на ньютоновских “больших” расстояниях друг от друга, той же самой, что и ИСО ньютоновского и галилеевского объектов, для которых 
при любом (галилеевском или ньютоновском) расстоянии, где 1 - ньютоновский объект?”.
Ответ такой:
“Да, если масса одного ньютоновского объекта много больше массы другого, а ньютоновское расстояние удовлетворяет соотношению:
,
т.е. достаточно велико, чтобы, в пределах точности вычислений, определяемой допускаемыми погрешностями 
, можно было принять , а саму ”.
С указанной выше точностью именно такой случай имеет место в ньютоновских окрестностях Земли, что и позволило самому Ньютону понять то обстоятельство, что взаимодействие тел простирается на ньютоновские расстояния.
Следует, однако, помнить и другие возможные варианты ответа:
“Нет, если оба ньютоновских объекта близки друг другу по массе 
, при любом расстоянии между ними, кроме , когда оба 
,
29-04-2015, 03:08