1. если все значения признака умножить на с, то и среднее умножается на С.
2. пусть исходные данные представлены следующим образом ![]() , т.е. данные разбиты на q групп . Взвешенное среднее арифметическое из групповых или частотных средних будет равняться общей средней.
, т.е. данные разбиты на q групп . Взвешенное среднее арифметическое из групповых или частотных средних будет равняться общей средней.
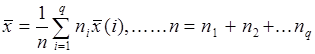
4. сумма взвешенных отклонений значений признака от общей средней арифметической равна 0: 
5. сумма квадратов взвешенных отклонений значений признака от ![]() меньше аналогичной суммы от любой другой меры положения
меньше аналогичной суммы от любой другой меры положения
![]()
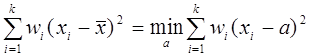 , разность между этими суммами равна
, разность между этими суммами равна ![]() .
.
Рассмотрим среднее гармоническое q=-1.
![]()
Свойства среднего гармонического:
1. взвешенная гармоническая из групповых гармонических равна общей гармонической 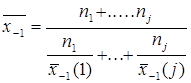 .
.
Применение того или иного вида весов зависит от представления значений признака.
Примеры.
Таким образом, если между показателями существует обратная зависимость как например между числом изготовленных деталей и затратами времени на одно изделие, то надо использовать среднее гармоническое. А если между показателями существует прямая зависимость, например между индивидуальными зарплатами и фондом зарплат, то применяется среднее арифметическое.
Рассмотрим геометрическое среднее:
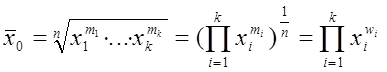
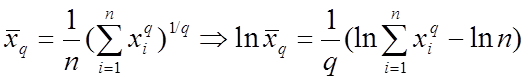
Вычислим предел:
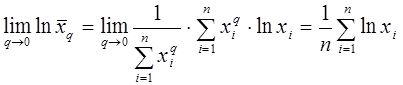
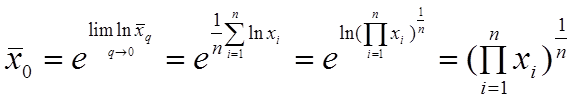
6. Свойства среднего геометрического:
1. общее среднее геометрическое может быть найдено по формуле 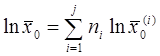 .
.
2. если кроме признака х рассмотреть признак у со значениями у(1), у(2),......,![]() , то имеем
, то имеем ![]()
3. если есть несколько совокупностей ![]() , то имеем
, то имеем ![]()
Среднее геометрическое применяется для расчета среднего коэффициента или среднего темпа роста
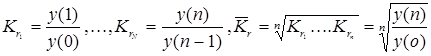
пример.
Пусть известно, что за 5 лет выпуск промышленной продукции предприятия вырос в 1.5 раза, тогда средний ежегодный коэффициент роста ![]() , т.е. 108,4 %, а средний ежегодный прирост равен 8,4%.
, т.е. 108,4 %, а средний ежегодный прирост равен 8,4%.
Среднее квадратическое q=2.
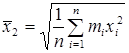
Обычно применяются, если в качестве ![]() берутся отклонения значений признака от среднеарифметических
берутся отклонения значений признака от среднеарифметических 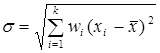 .
.
Если n<=30, то применяется исправленное среднеквадратичное отклонение 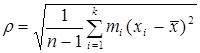 .
.
7.Структурные (порядковые) характеристики.
Квантили - порядковые характеристики, то есть значения признака, занимающие определенное место в ранжированной совокупности (упорядоченной).
Медиана.
Медиана - значение изучаемого признака, приходящееся на середину ранжированной совокупности.
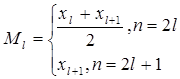
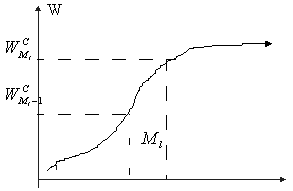
При вычислении медианы интервального вариационного ряда, сначала находят медианный интервал ![]() , где h - длина медианного интервала. Для этого можно использовать кумулятивное распределение частот или относительных частот. Медианному интервалу соответствует тот, в котором содержится накопленная равная 1/2.
, где h - длина медианного интервала. Для этого можно использовать кумулятивное распределение частот или относительных частот. Медианному интервалу соответствует тот, в котором содержится накопленная равная 1/2.
Внутри найденного интервала расчет медианы производится по формуле:
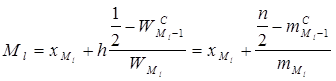 , где
, где ![]() - кумулятивная частота интервала, предшествующего медианному,
- кумулятивная частота интервала, предшествующего медианному, ![]() - относительная частота медианного инетрвала.
- относительная частота медианного инетрвала.
Сумма взвешенных абсолютных отклонений вариант от медианы меньше аналогичной суммы отклонений вариант от любой другой меры положения вариационного ряда.
Это свойство можно использовать при проектировании оптимального (в некотором смысле) расположения остановок общественного транспорта, складских помещений, бензозаправок и т.д.
пример.
Прибыль компаний: Ме=500 +500*(50-44)/(76-44)=593.75 млн. Это означает, что 50% компаний имеет прибыль меньше 593.75 млн.
Оценки студентов: Ме=4
Квартили.
Квартили - порядковые характеристики, отделяющие четверти ранжированных совокупностей.
1 квартиль или нижний отделяет четверть ранжированной совокупности снизу и вычисляется по формуле:
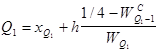 (для интервального)
(для интервального)
Медиану можно рассматривать как второй квартиль.
Верхний квартиль 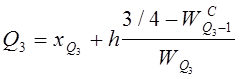
Мода.
Мода - наиболее часто встречающееся в совокупности значение признака. Для дискретного вариационного ряда мода определяется по частотам вариант и соответствует варианте с максимальной частотой. При определении моды обычно применяют следующие соглашения:
1. если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды.
2. если две соседних варианты имеют одинаковую доминирующую частоту, что мода вычисляется как среднее арифметическое этих вариант.
3. если две не соседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называется бимодальным.
4. если таких вариант более двух, то ряд - полимодальный.
В случае интервального вариационного ряда с равными интервалами модальный интервал определяется по наибольшей частоте, а при неравных интервалах - по наибольшей плотности.
При равных интервалах мода внутри модального интервала может определяться по следующей формуле:
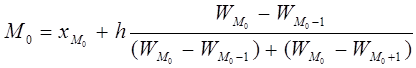
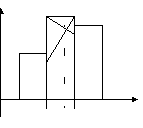
Данная формула получена исходя из допущения, что в модальном и двух соседних интервалах кривая распределения представляет собой параболу второго порядка. Тогда мода находится как вершина параболы. Для графического определения моды используют 3 соседних столбца гистограммы (самый высокий и 2 прилегающих к нему).
При вычислении моды в формуле можно использовать не только относительные, но и другие частоты.
пример.
Прибыль 100 компаний - Мо=0+500*(41-1)/(41-1+41-32)=408.16 млн.
Оказывается, по расположению средней арифметической, моды и медианы можно судить о форме распределения. Если оно симметричное, то все три величины равны.
В практике мода и медиана иногда используются вместо средней арифметической или вместе с ней. Фиксируя средние цены товаров или продуктов на рынке записывают наиболее часто встречающуюся цену на рынке (моду цены).
Робастные характеристики для оценки среднего арифметического.
В ряде случаев в изучаемой совокупности имеется небольшое число элементов с чрезвычайно большим или чрезмерно малым значением исследуемого признака.
В этих случаях в дополнение к среднему арифметическому целесообразно вычислить моду и медиану, которые в отличие от среднего не зависят от крайних, не характерных для совокупности значений признака. Мода и медиана относятся к классу так называемых “робастных характеристик”, т.е. не чувствительных к аномальным значениям признака. Рассмотрим робастные характеристики, применяемые для оценки среднего арифметического:
1. усеченное среднееарифметическое порядка ![]()
![]()
Пусть имеем ряд значений признака, упорядоченный в возрастающем порядке
![]() , упорядоченный в возрастающем порядке. Пусть первые x(1),...,x(m) - аномально маленькие, x(n-m+1),...,x(n) - аномально большие.
, упорядоченный в возрастающем порядке. Пусть первые x(1),...,x(m) - аномально маленькие, x(n-m+1),...,x(n) - аномально большие.
![]() - указывает долю отбрасываемых значений признака.
- указывает долю отбрасываемых значений признака.
2. среднее по Виндору
Отличается от усеченного тем, что аномальные значения признака не отбрасываются, а полагаются крайним значениям, принимаемым на обработку.
x(1)=x(2)...=x(m)=x(m+1)
x(n)=x(n-1)=...=x(n-m+1)=x(n-m)
![]()
примеры.
8.Характеристики рассеяния.
Средняя величина признака, а также его мода и медиана в двух совокупностях могут быть одинаковыми. но в одном случае значения признака могут мало отличаться от среднего, а в другом эти значения могут быть велики.
пример.
Пусть имеются данные о стаже работы в 2 бригадах.
| стаж | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | средн. |
| 1 бр. | 1 | 2 | 3 | 3 | 4 | 9 | 10 | 12 | 13 | 15 | 7.2 |
| 2 бр. | 6 | 6 | 7 | 7 | 7 | 7 | 8 | 8 | 18 | 8 | 7.2 |
Простейшим из показателей является вариационный размах R=Xmax-Xmin. Размах выборки дает лишь самое общее представление о размерах вариации, так как показывает насколько отчаются друг от друга крайние значения, но не указывают насколько велики отклонения вариант друг от друга внутри этого промежутка. Более точным будет такой показатель, который учитывает отклонение каждой из вариант от средней величины.
Выделяют среднее линейное отклонение ![]() , либо среднеквадратичное отклонение
, либо среднеквадратичное отклонение ![]() .
.
Если объем выборки невелик, то в качестве оценки дисперсии рассматривают ![]()
![]() .
.
пример.
Для вычисления дисперсии можно использовать формулу 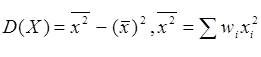 .
.
Основные свойства дисперсии:
1. ![]()
2. ![]()
3. ![]()
4. 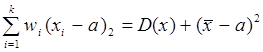 , то есть дисперсия принимает минимальное значение среди всевозможных взвешенных квадратов отклонений значений признака от любой другой меры положения а.
, то есть дисперсия принимает минимальное значение среди всевозможных взвешенных квадратов отклонений значений признака от любой другой меры положения а.
5. правило сложения дисперсий
Пусть ряд значений признака состоит из j однородных групп: x(1),...,X(n1),...X(n1+n2),...X(n),n=n1+n2+...+nj. Обозначим дисперсии групп D1,...Dj/
Надо найти общую дисперсию.
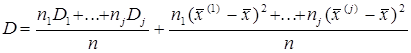
![]() , т.е. общая дисперсия равна сумме внутригрупповой и внешне групповой дисперсий.
, т.е. общая дисперсия равна сумме внутригрупповой и внешне групповой дисперсий.
Таким образом общая дисперсия равна взвешенной сумме групповых дисперсий и взвешенной сумме квадратов отклонений групповых средних от общей средней. Первое слагаемое выражает величину дисперсии внутри частей совокупности, а второе- различие между этими частями.
пример.
Каждая из перечисленных дисперсий имеет вполне определенный смысл: общая дисперсия показывает величину вариации зарплаты, которая вызвана всеми факторами, влияющими на размер зарплаты. (число обслуживаемых станков, различия в опыте и т.д.) Групповые дисперсии показывают величину вариации, которая вызвана многими причинами кроме различий в числе обсуживаемых станков, так как внутри группы все рабочие обслуживают одинаковое количество станков. Средняя из групповых вариаций вызвана не различиями в числе обслуживаемых станков по всему числу рабочих, различия по числу станков.
Чем больше межгрупповая дисперсия ![]() по сравнению
по сравнению ![]() , тем больше влияние группировочного признака на величину исследуемого признака.
, тем больше влияние группировочного признака на величину исследуемого признака.
Если группировать рабочих внутри каждой группы по другому признаку, оказывающему влияние на заработок, например по уровню квалификации, то можно из внутригрупповых дисперсий выделить дисперсию, показывающую величину вариации, вызванной вторым группировочным признаком и дисперсию остаточную, характеризующую вариацию за счет всех причин, кроме 2 группировочных признаков. Теоретически такую комбинационную группировку можно продолжать до тех пор, пока не будут исчерпаны все причины, воздействующие на исследуемый признак. Общая дисперсия в этот случае будет представлена как сумма дисперсий, характеризующих вариацию, вызванную каждой из причин.
Кроме абсолютных для характеристики совокупности значений признаков применяются относительные показатели.
Коэффициент вариации ![]() .
.
Используется для сравнения размеров вариации в вариационных рядах с различными средними, а также для сравнения вариаций разных показателей в оной и той же совокупности. Он отражает состояние между вариацией выборки и ее центром.
1. ![]() <=30% - выборка имеем довольно большую степень концентрации относительного среднего.
<=30% - выборка имеем довольно большую степень концентрации относительного среднего.
2. 30%<=![]() <=100% - степень концентрации допустимая.
<=100% - степень концентрации допустимая.
3. ![]() >=100% - делается вывод о неоднородности выборки.
>=100% - делается вывод о неоднородности выборки.
пример.
Реже используются следующие коэффициенты:
1. Коэффициент вариации по размаху ![]()
2. Коэффициент вариации по среднему линейному отклонению ![]()
3. Квартильное отклонение ![]() .
.
9.Характеристики формы распределения вариационного ряда.
Существуют 2 основных характеристики: коэффициент ассиметрии и коэффициент эксцессов, которые характеризуют соответсвенно скошенность и крутость распределения.
Моментом порядка р распределения вариационного ряда называется
![]()
В зависимости от значения а общая схема моментов разбивается на 3 подсистемы.
1. а=0, получаем систему начальных моментов 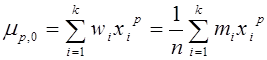
2. ![]() а=x, получаем систему центральных моментов
а=x, получаем систему центральных моментов 
3. а=с=const, обычно С близкое к середине вариационного ряда. Получаем систему условных моментов. Она применяется для упрощения расчетов.
Центральные моменты 3 и 4 порядков используются для характеристики ассиметрии и эксцесса распределения вариационного ряда.
10.Сравнение эмпирического и теоретического распределений вариационных рядов.
1. дискретные вариационные ряды
Пусть имеется вариационный ряд. Предположим, что признак Х распределен по некоторому вероятностному закону Р.![]()
Р:
| х | х1 | х2 | .... | xk |
| р | p1 | p2 | ..... | pk |
По теоретическому распределению Р можно построить так называемое выравнивающие или теоретические частоты ![]() . Если отличия между теоретическими и эмпирическими частотами небольшое, то можно считать, что Х распределен по закону Р.
. Если отличия между теоретическими и эмпирическими частотами небольшое, то можно считать, что Х распределен по закону Р.
2. критерий согласия Пирсона
Объективную оценку близости эмпирических частот к теоретическим можно получить с помощью определенных критериев близости, называемых критериями согласия. Существует множество таких критериев. Критерий Пирсона основан на следующем:
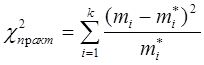 .
.
Существуют значения (табличные) для соответствующего числа степеней свободы К и уровня значимости ![]() . По таблице находятся
. По таблице находятся ![]()
K=k-1-r, где r - число общих характеристик теоретического распределения, принятых равными соответствующим эмпирическим.
11.Оценивание параметров распределений по выборке. Доверительные интервалы.
1. требования к оценкам
Пусть требуется изучить количественный признак генеральной совокупности. Допустим из теоретических соображений удалось установить какое именно распределение имеет признак. Естественна задача оценки параметров этого распределения.
Требования к оценкам:
1. несмещенность или асимптотическая несмещенность
![]()
2. состоятельность
![]()
Требование состоятельности применяется к большим объемам.
3. эффективность
Эффективной называют оценку, которая при заданном объеме выборки n имеет min дисперсию.
2. надежность оценок
Оценку, определяемую одним числом называют точечной. При выборках малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольших объемах выборки пользуются интервальными оценками, которые определяются 2 числами - концами интервала. Эти оценки позволяют установить точность и надежность оценок.
Пусть ![]() =const,
=const, ![]() тем точнее определяет
тем точнее определяет ![]() , чем меньше (
, чем меньше (![]() -
-![]() ). Если есть величина
). Если есть величина ![]() >0, (
>0, (![]() -
-![]() )<
)<![]() , то чем меньше
, то чем меньше ![]() , тем точнее оценка.
, тем точнее оценка.
![]() - надежность оценки. Обычно надежность задается наперед
- надежность оценки. Обычно надежность задается наперед ![]() =95-99%. Величину
=95-99%. Величину ![]() называют уровнем значимости.
называют уровнем значимости.
![]() , интервал
, интервал ![]() - доверительный. Концы этого интервала - случайные величины и называются доверительными границами, они могут меняться от выборки к выборке. Говорят, что наш доверительный интервал с вероятностью
- доверительный. Концы этого интервала - случайные величины и называются доверительными границами, они могут меняться от выборки к выборке. Говорят, что наш доверительный интервал с вероятностью ![]() покрывает
покрывает ![]() .
.
29-04-2015, 03:08
