ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Медицинский институт
Кафедра гигиены, общественного здоровья и здравоохранения
( зав. кафедрой к.м.н. А.П. Дмитриев)
СРЕДНИЕ ВЕЛИЧИНЫ, ОЦЕНКА РАЗНООБРАЗИЯ ПРИЗНАКА В ВАРИАЦИОННОМ РЯДУ.
Учебно-методическое пособие для студентов
(VШ семестр)
г. Пенза, 2005.
Информационный лист:
Учебно-методическое пособие “Средние величины, оценка разнообразия признака в вариационном ряду.” подготовлено кафедрой гигиены, общественного здоровья и здравоохранения Пензенского государственного университета (заведующий кафедрой, к.м.н. Дмитриев А.П.).
В составлении принимали участие: к.м.н. Зубриянова Н.С. , Дмитриев А.П. (ответственный за подготовку Зубриянова Н.С.).
Учебно-методическое пособие подготовлено в соответствии с «Программой по общественному здоровью и здравоохранению ” для студентов лечебных факультетов высших медицинских учебных заведений”, разработанной Всероссийским учебно-научно-методическим Центром по непрерывному медицинскому и фармацевтическому образованию Минздрава России и УМЦпкп и утвержденной Руководителем департамента образовательных медицинских учреждений и кадровой политики Н.Н. Володиным в 2000 г.
Данное Учебно-методическое пособие подготовлено для студентов для самостоятельной подготовки к практическим занятиям по указанной теме.
Тема: Средние величины, оценка разнообразия признака в вариационном ряду.
Оценка достоверности
Вопросы :
- методы расчета средних величин
- оценка достоверности относительных и средних величин
Продолжительность занятия : 4 часа
Самостоятельная работа : лабораторная работа №6
Теоретическая часть.
Средние величины
В клинической медицине и практике здравоохранения мы часто сталкиваемся с признаками, имеющими количественную характеристику (рост, число дней нетрудоспособности, уровень кровяного давления, посещения поликлиники, численность населения на участке и т.д.). Количественные значения могут быть дискретными или непрерывными. Пример дискретного значения – число детей в семье, пульс; пример непрерывного значения – артериальное давление, рост, вес (число может быть дробным, переходящим в следующее)
Каждое числовое значение единицы наблюдения называется вариантой (x). Если все варианты построить в возрастающем или убывающем порядке и указать частоту каждой варианты (p), то можно получить так называемый вариационный ряд .
Вариационный ряд, имеющий нормальное распределение, графически представляет собой колокол (гистограмма, полигон).
Для характеристики вариационного ряда, имеющего нормальное распределение (или распределение Гаусса-Ляпунова), всегда используются две группы параметров:
1.Параметры, характеризующие основную тенденцию ряда: средняя величина (`x ), мода(Мо), медиана (Ме).
2.Параметры, характеризующие рассеянность ряда: среднее квадратичное отклонение (d), коэффициент вариации (V).
Средняя величина (`x ) – это величина, определяющая одним числом количественную характеристику качественно однородной совокупности.
Мода (Мо) – чаще всего встречающаяся варианта вариационного ряда.
Медиана (Ме) – варианта, делящая вариационный ряд на равные половины.
Среднее квадратичное отклонение (d) показывает, как в среднем отклоняется каждая варианта от средней величины.
Коэффициент вариации ( V ) определяет изменчивость вариационного ряда в процентах и дает возможность судить о качественной однородности изучаемой совокупности. Целесообразно использовать для сравнения вариации различных признаков (а также степени изменчивости сильно отличающихся групп, групп особей разных видов, например, вес новорожденных и семилетних детей).
Лимиты или пределы (lim) – минимальное и максимальное значение вариант. простейший способ дать характеристику вариационному ряду, указать его размах, минимальное и максимальное значение ряда, т.е. его лимиты. Однако лимиты не указывают на то, как распределяются по изучаемому признаку отдельные члены совокупности, поэтому используют указанные выше две группы параметров вариационного ряда.
Имеются разные модификации вычисления параметров вариационного ряда. Их выбор зависит от самого вариационного ряда и технических средств.
В зависимости от того как варьирует признак – дискретно или непрерывно, в широком или узком диапазоне различают простой невзвешенный, простой взвешенный (для дискретных величин) и интервальный вариационный ряд (для непрерывных величин).
Группировку рядов проводят при большом числе наблюдений следующим путем:
1.Определяют размах ряда вычитанием минимальной варианты из максимальной.
2.Полученное число делят на желаемое число групп (минимальное число – 7, максимальное – 15). Так определяется интервал.
3.Начиная с минимальной варианты, строят вариационный ряд. Границы интервалов должны быть четкие, исключающие попадание одной и той же варианты в разные группы.
Вычисление параметров вариационного ряда ведется от центральной варианты. Если ряд непрерывный, то центральная варианта вычисляется как полусумма начальных вариант предыдущей и последующей групп. Если это прерывный ряд, то центральная варианта вычисляется как полусумма начальной и конечной вариант в группе.
Вычисление параметров вариационного ряда
| Вид вариационного ряда |
p |
`x |
d |
| Простой невзвешенный |
1 |
|
± |
| Простой взвешенный |
>1 |
|
± |
| Сгруппированный |
>1 |
|
± |
Алгоритм вычисления параметров простого невзвешенного вариационного ряда:
1. Располагают варианты в возрастающем порядке
2. Суммируют все варианты (Sx);
3. Разделив сумму на число наблюдений, получают невзвешенную среднюю ![]() ;
;
4. Вычисляют порядковый номер медианы (Ме);
5. Определяют варианту медианы (Ме)
6. Находят отклонение (d) каждой варианты от средней (d = x -`x)
7. Возводят отклонение в квадрат (d2 );
8. Суммируют d2 (Sd2 );
9. Вычисляют среднее квадратичное отклонение по формуле: ±![]() ;
;
10. Определяют коэффициент вариации по формуле: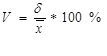 .
.
11. Делают вывод о полученных результатах.
Примечание: в однородной статистической совокупности коэффициент вариации бывает 5-10%, 11-20% - средняя вариации, более 20% - высокая вариация.
Пример:
В отделении реанимации и интенсивной терапии было проведено лечение 9 больных с сосудистым поражением мозга. Длительность лечения каждого больного в днях: 7, 8, 12, 6, 4, 10, 9, 5,11.
1.Строим вариационный ряд (x): 4,5,6,7,8,9,10,11,12
2.Вычисляем сумму вариант: Sx = 72
3.Вычисляем среднее значение вариационного ряда: ![]() =72/9=8 дней;
=72/9=8 дней;
4.![]() ;
;
5.Меn =5 =8 дней;
6,7,8
| x |
d |
d2 |
| 4 |
-4 |
16 |
| 5 |
-3 |
9 |
| 6 |
-2 |
4 |
| 7 |
-1 |
1 |
| 8 |
0 |
0 |
| 9 |
+1 |
1 |
| 10 |
+2 |
4 |
| 11 |
+3 |
9 |
| 12 |
+4 |
16 |
| S=72 |
S=0 |
Sd2 =60 |
9. ![]()
![]() (дней);
(дней);
10. Коэффициент вариации равен: ![]() ;
;
Алгоритм вычисления параметров простого взвешенного вариационного ряда:
1.Располагают варианты в возрастающем порядке с указанием их частоты (p);
2.Перемножают каждую варианту на свою частоту (x*p);
3.Суммируют произведения xp (Sxp);
4.Вычисляют среднюю величину по формуле (`x)= ![]() ;
;
5.Находят порядковый номер медианы ![]() ;
;
6.Определяют варианту медианы (Ме);
7.Чаще всего встречающуюся варианту принимают за моду (Мо);
8.Находят отклонения d каждой варианты от средней (d = x - `x);
9.Возводят отклонения в квадрат (d2 );
10. Перемножают d2 на p (d2 *p);
11. Суммируют d2 *p (Sd2 *p);
12. Вычисляют среднее квадратичное отклонение (s) по формуле: ±![]() ;
;
13. Определяют коэффициент вариации по формуле: 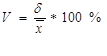 .
.
Пример.
Измерялось систолическое артериальное давление у девушек в возрасте 16 лет.
| Систолическое артериальное давление, мм рт.ст. x |
Число обследованных, p |
x*p |
d |
d2 |
d2 *p |
| 96 |
2 |
192 |
-11.4 |
130.0 |
260.0 |
| 98 |
3 |
294 |
-9.4 |
88.4 |
265.2 |
| 100 |
4 |
400 |
-7.4 |
54.8 |
219.2 |
| 102 |
6 |
612 |
-5.4 |
29.2 |
175.2 |
| 106 |
10 |
1060 |
-1.4 |
2.0 |
20.0 |
| 108 |
24 |
2592 |
+0.6 |
0.4 |
9.6 |
| 110 |
6 |
660 |
2.6 |
6.8 |
40.8 |
| 112 |
4 |
448 |
4.6 |
21.2 |
84.8 |
| 114 |
3 |
342 |
6.6 |
43.6 |
130.8 |
| 118 |
3 |
354 |
10.6 |
112.4 |
337.2 |
| 120 |
2 |
240 |
12.6 |
158.8 |
317.6 |
| n=67 |
Sxp=7194 |
Sd2 p=1860.4 |
![]() мм рт.ст.;
мм рт.ст.;
![]() мм рт.ст.
мм рт.ст.
![]() ;
;
Ме=108 мм рт.ст.; Мо=108 мм рт.ст.
Алгоритм вычисления параметров сгруппированного вариационного ряда способом моментов:
1.Расположить варианты в возрастающем порядке с указанием их частоты (р)
2.Провести группировку вариант
3.Вычислить центральную варианту
4.Варианту с самой высокой частотой принимают за условную среднюю (А)
5.Вычислить условное отклонение (а) каждой центральной варианты от условной средней (А)
6.Перемножают а на р (а*р)
7.Суммируют произведения ар
8.Определяют величину интервала y путем вычитания центральной варианты из предыдущей
9.Вычисляют среднюю величину по формуле:
![]() ;
;
10. Для вычисления условного квадратичного отклонения условные отклонения возводят в квадрат (а2 )
11. Перемножают а2 *р
12. Суммируют произведения а*р2
13. Вычисляют среднее квадратичное отклонение по формуле
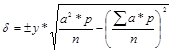
Пример
Имеются данные мужчин в возрасте 30-39 лет
| масса, кг х |
Число обследованных р |
Серединная варианта хс |
а |
а2 |
а2 *р |
а*р |
Накопленные частоты |
| 45-49 |
1 |
47,5 |
-4 |
16 |
16 |
-4 |
1 |
| 50-54 |
3 |
52,5 |
-3 |
9 |
27 |
-9 |
4 |
| 55-59 |
7 |
57,5 |
-2 |
4 |
28 |
-14 |
11 |
| 60-64 |
10 |
62,5 |
-1 |
1 |
10 |
-10 |
21 |
| 65-69 |
19 |
67,5 |
0 |
0 |
0 |
0 |
40 |
| 70-74 |
15 |
72,5 |
1 |
1 |
15 |
15 |
55 |
| 75-79 |
12 |
77,5 |
2 |
4 |
48 |
24 |
67 |
| 80-84 |
6 |
82,5 |
3 |
9 |
54 |
18 |
73 |
| 85-89 |
3 |
87,5 |
4 |
16 |
48 |
12 |
76 |
| сумма |
246 |
32 |
![]() - средняя арифметическая
- средняя арифметическая
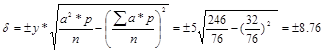 ; - среднее квадратичное отклонение;
; - среднее квадратичное отклонение; ![]() - ошибка средней
- ошибка средней
Оценка достоверности
Статистическая оценка достоверности результатов медико-статистического исследования складывается из ряда этапов – точность результатов зависит отдельных этапов.
При этом встречаются две категории ошибок: 1) ошибки, которые нельзя заранее учесть математическими методами (ошибки точности, внимания, типичности, методические ошибки и т.д.); 2) ошибки репрезентативности, связанные с выборочным исследованием.
Величина ошибки репрезентативности определяется как объемом выборки, так и разнообразием признака и выражается средней ошибкой. Средняя ошибка показателя вычисляется по формуле:
![]() ;
;
где m – средняя ошибка показателя;
p – статистический показатель;
q – величина обратная p (1-p, 100-p, 1000-p, и т.д.)
n – число наблюдений.
При числе наблюдений менее 30 в формулу вводится поправка:
![]() ;
;
Ошибка средней величины исчисляется по формулам:
![]() ;
; ![]() ;
;
где s - среднее квадратичное отклонение;
n – число наблюдений.
Пример 1.
Из стационара выбыло 289 человек, умерло – 12.
Летальность составит:
![]() ;
; ![]() ;
;
![]()
При проведении повторных исследований средняя (М) в 68% случаев будет колебаться в пределах ±m, т.е. степень вероятности (p), с которой мы получим такие доверительные границы средней, равна 0,68. Однако такая степень вероятности обычно не удовлетворяет исследователей. Наименьшей степенью вероятности, с которой хотят получить определенные границы колебания средней (доверительные границы), является 0,95 (95%). В этом случае доверительные границы средней должны быть расширены путем умножения ошибки (m) на доверительный коэффициент (t).
Доверительный коэффициент (t) – число, показывающее, во сколько раз нужно увеличить ошибку средней величины, чтобы при данном числе наблюдений с желаемой степенью вероятности (p) утверждать, что средняя величина не выйдет за получаемые таким образом пределы.
При p=0.95 (95%) t=2, т.е. M±tm=M+2m;
При p=0.99 (99%) t=3, т.е. M±tm=M+3m;
Сравнение средних показателей
При сравнении двух средних арифметических (или двух показателей), вычисленных за различные периоды времени или в несколько отличающихся условиях, определяется существенность различий между ними. При этом применяется следующее правило: разница между средними (или показателями) считается существенной в том случае, если арифметическая разность между сравниваемыми средними (или показателями) будет больше, чем два квадратных корня из суммы квадратов ошибок этих средних (или показателей), т.е.
![]() (для сравниваемых средних);
(для сравниваемых средних);
![]() (для сравниваемых показателей).
(для сравниваемых показателей).
Определение достоверности средней при малом числе наблюдений (малая выборка).
При проведении исследований их объем не превышает 10-30 случаев. Такой объем наблюдений называется малым (или малой выборкой).
при определении статистической достоверности средней, полученной при малом числе наблюдений пользуются следующими формулами:
![]() ; где
; где ![]() ;
;
d – отклонение варианты (V) от средней величины (M),
n – число наблюдений;
t – доверительный коэффициент, определяемый по специальной таблице Стьюдента (приложение).
Пример.
Измерен пульс у 9 человек. Надо вычислить среднюю частоту пульса и определить ее статистическую достоверность.
1.Строиться вариационный ряд, вычисляется средняя (М) и среднее квадратичное отклонение (s).
| V |
d=V-M |
d2 |
| 63 |
-5 |
25 |
| 68 |
0 |
0 |
| 65 |
-3 |
9 |
| 65 |
-3 |
9 |
| 60 |
-8 |
64 |
| 70 |
+2 |
4 |
| 70 |
+2 |
4 |
| 75 |
+7 |
49 |
| 76 |
+8 |
64 |
| SV=612, n=9 |