Микрокривизна и физическая микронеоднородность собственных пространств протонов и нейтронов из-за возрастания от периферии к центру густоты их индивидуальных спиральных витков также имеют место. Однако, эти локализованные неоднородности не возможно определить решением уравнений гравитационного поля. Ведь ОТО, как и механика и термодинамика, оперирует лишь среднестатистическими параметрами и, как и СТО (на неадекватность описания которой пространствено-временных отношений в микромире обратил внимание Гейзенберг [45]) предусматривает лишь абсолютно сплошную и локально равномерную заполненность пространства материей. И более того, микрокривизна и физическая микронеоднородность пространства сильно изменяются в процессе взаимодействия элементарных частиц.
Поэтому, уравнения квантовой физики, которые в неявном виде учитывают (или должны учитывать) микрокривизну и физическую микронеоднородность пространства, приходится решать совместно с уравнениями ренормгруппы. А это значит, что метрические отношения в микромире являются весьма нетривиальными (Зельманов предполагает, что они вообще отсутствуют [26, 46], а Менгер предлагает ввести статистическое понятие расстояния между точками [47]) и не позволяющими в обычном виде сформулировать законы сохранения. Таким образом, в жесткой СО вещества пространственные распределения значений микрокривизны и физической микронеоднородности ее пространства (в отличие от распределений макрокривизны и физической макронеоднородности) не являются стабильными во времени. И это приводит к несохранению мгновенных значений энергии, как фотонов, так и элементарных частиц. И, следовательно, в микромире могут сохраняться лишь средние значения (математические ожидания) энергии элементарных частиц [17].
Погрешность определения этого среднего значения энергии: ΔEmin=ħ/Δt тем меньше, чем больше промежуток времени, за который оно определяется. Поэтому соотношения неопределенностей Гейзенберга фактически устанавливают форму записи законов сохранения в микромире (в субатомной физике). Статистический характер законов сохранения обусловлен двумя следующими основными факторами – действием этих законов в неотрывном от вещества а, следовательно, и от естественных часов этого вещества его собственном физическом пространстве (а не в собственном метрическом пространстве, в котором вещество деформируется и в котором, следовательно, его естественные часы не являются неподвижными) [17, 18, 48] и стохастичностью микроструктуры физического пространства, которое в собственной коллективной СО всего вещества должно быть неотрывным и от каждой элементарной частицы вещества. Возможность введения понятия неопределенной системы координат (стохастической СО) рассматривал Широков [49].
Нити вихрей сходящихся спиральных волн, соответствующих, согласо 6), отрицательно заряженным частицам, устойчивы лишь в пространстве или же в микроподпространствах, в которых ∂r/∂R>0. Нити вихрей расходящихся спиральных волн, соответствующих положительно заряженным частицам, устойчивы лишь в пространстве или же в микроподпространствах, в которых ∂r/∂R<0. Только в этих пространствах или микроподпространствах их фазовые траектории наматываются на предельные циклы. Поэтому, положительно заряженные кварки абсолютно стабильных частиц (протонов и нейтронов) самоизолируются от внешнего пространства метрически сингулярной поверхностью и витки их спиральных волн стекают к псевдогоризонту будущего микроподпространства, ограниченного этой сингулярной поверхностью. Ввиду этого шварцшильдоподобный радиус сильной гравитации и оказывается порядка размеров протона и нейтрона [2]. Данная сингулярная поверхность является стоком витков спиральных волн во внешнем пространстве и их истоком в ею ограничиваемом микроподпространстве.
В этом микроподпространстве сингулярная поверхность воспринимается как выпуклая поверхность, которая содержит внутри себя всю Вселенную. Поэтому, в СО положительно заряженного кварка протона, охваченного сингулярной поверхностью, Вселенная может рассматриваться как отрицательно заряженный барион. И это является одной из причин утопического рассматривания элементарных частиц как микровселенных [2].
В общем случае возможны две различные топологии. Если положительно заряженный кварк имеет полую топологическую форму и квазиконцентричен охватывающей его сингулярной поверхности в абсолютном пространстве, то в его СО Вселенная будет им охвачена. При отсутствии же этой квазиконцентричности будет иметь место планетарная модель. Положительно заряженный кварк будет как бы вращаться вокруг отрицательно заряженной Вселенной. Переход от одной топологии к другой соответствует изменению метастабильного состояния кварка (изменению значений его квантовых чисел) и не обязательно должен быть связан с поглощением или испусканием им каких-либо специфических частиц или квазичастиц. Отрицательно заряженный d-кварк протона, плененный этой же сингулярной поверхностью, может быть подвергнутым дополнительному пленению (как в матрешке) сингулярной поверхностью одного из двух положительно заряженных u-кварков. Поэтому, эти два u-кварка будут находиться не в одинаковых квантовых состояниях (будут иметь неодинаковый «цвет»). Сам же d-кварк виду этого может являться всего лишь s-кварком, дополнительно охваченным «экранирующей» его странность сингулярной поверхностью какого-либо другого кварка.
Эти сингулярные поверхности могут быть сферическими и эллипсоидальными (при стремлении спиральной волны к вырождению в концентрические волны пейсмекера [30] в СО, в которой образуемая ею элементарная частица неподвижна) или же торическими, а возможно – и быть замкнутыми поверхностями более сложной формы в случае образования вихревых узлов. Совместное пленение такой сингулярной поверхностью нескольких кварков делает требование скрученности вихревых колец спиральных волн этих кварков не строго обязательным (избыточным). Поэтому нельзя исключать возможность самоорганизации всех или же только некоторых типов кварков и в виде простых вихревых колец.
Аналогичная картина имеет место и во внутреннем полупространстве полого тела. Изложенные же здесь физические представления хорошо дополняют известные теории элементарных частиц при неизбежном их переосмыслении (а возможно – и с учетом модернизации некоторых из них).
В соответствии со всем этим элементарные частицы и состоящее из них вещество являются устойчивыми только во внешнем пустом пространстве и во внешнем полуслое полого тела. Во внутреннем пустом пространстве и во внутреннем полуслое полого тела, наоборот, устойчивыми являются лишь античастицы и состоящее из них антивещество (см. рис. 1).
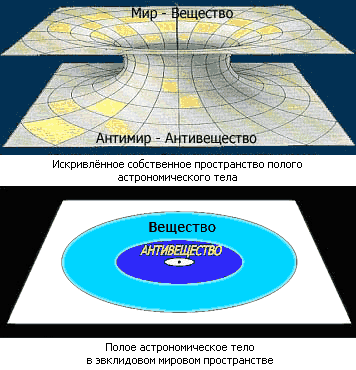
Рис. 1. Сингулярная поверхность
И, поэтому, срединная сингулярная поверхность полого тела является естественным барьером между веществом и антивеществом, который предохраняет их от катастрофической аннигиляции. Спорадическое же просачивание вещества и антивещества через этот барьер принципиально возможно (даже без привлечения квантово-механических представлений о движении), вследствие не полностью взаимно координируемого (без этого просачивания) остывания внешней и внутренней частей не абсолютно холодного полого тела. Это остывание нарушает общее равновесие и, тем самым, приводит к радиальному мигрированию сингулярной поверхности относительно вещества и антивещества. Благодаря аннигиляции вещества и антивещества, которая является следствием этого просачивания, возможно неограниченное во времени поддерживание слабой излучательной способности полого тела со сколь угодно холодными граничными поверхностями. В нежестких и квазижестких собственных СО остывающих полых тел фотометрический радиус срединной сингулярной поверхности непрерывно уменьшается. И каждому конкретному значению этого радиуса (как и значению радиуса горизонта видимости [18, 48]) могут быть сопоставлены все события, которые совпадают друг с другом во внутренней СО вещества. Из-за постепенного перемещения срединной сингулярной поверхности остывающего полого тела в его собственном пространстве значение скорости света на этой поверхности (как и на сингулярных поверхностях псевдогоризонтов прошлого и будущего [48]) в нежестких и квазижестких СО может быть сколь угодно малым, однако, не нулевым. Это обуславливает возможность беспрепятственного преимущественно одностороннего преодоления барьера между веществом и антивеществом, а именно, – возможность непрерывного проникновения лишь антивещества к веществу (во внешнюю часть полого тела). Тем самым, гарантируется непрерывное протекание постепенной аннигиляции вещества и антивещества в горячих полых телах. И, следовательно, основным источником энергии полых тел является аннигиляция вещества и антивещества.
Следует отметить, что до момента разрыва преимущественно водородно-гелиевого континуума Вселенной на отдельные газовые скопления не было антивещества во Вселенной. Первичная самоорганизация антивещества могла иметь место только вследствие возникновения сверхвысоких собственных значений плотности вещества, давления и температуры, а, следовательно, – и возникновения критической плотности энергии тормозного и теплового электромагнитных излучений и области пространства с неустойчивой сфероцилиндрической метрикой в центре гигантских газовых скоплений. Поэтому возникновение первичного («затравочного») антивещества привело к преобразованию неустойчивой однородной сфероцилиндрической метрики сначала в топологически неоднородную, а затем и в необычную метрику его собственного пространства. И оно могло иметь место вследствие рождения в фотонном газе пар частиц и античастиц, обладающих соответственно обычной и необычной метрикой собственных микроподпространств и, поэтому, не успевающих аннигилировать друг с другом. Объединение микроподпространств с необычной метрикой в единый пространственный континуум привело к локализации сингулярного состояния материи лишь на сферической сингулярной поверхности, которая стала «раздуваться» (увеличивать свой радиус) в абсолютном пространстве. Преобразование как возникших, так и ранее существовавших элементарных частиц в античастицы происходило по мере раздувания сингулярной поверхности благодаря обращению волнового фронта их спиральных волн.
Отдельные газовые скопления катастрофически самосжались в собственном пространстве благодаря возникновению и стремительному возрастанию сферически симметричной физической макронеоднородности пространства, которая привела к несохранению импульса в пространстве. Самосжатие газовых скоплений реализовывалось из-за накопления как прироста импульса направленных внутрь (центростремительных), так и убыли импульса направленных наружу (центробежных) виртуальных фотонов в процессе ван-дер-ваальсового электромагнитного взаимодействия молекул газа. Физическая макронеоднородность пространства (возникшая лишь в процессе этого и отождествляемая с гравитационным полем) привела и к поляризации физических микронеоднородностей пространства, которые сформированы атомами. Поэтому, виртуальные π-мезоны и фотоны, осуществляющие внутриатомные взаимодействия между протонами и соответственно нейтронами и электронами [18], также участвовали в приталкивании атомов к центру газового скопления. Они и сейчас участвуют в вызывании свободного падения тела и в приведении тела в движение под действием любых негравитационных сил и косвенно несут ответственность за инертность атомов из-за конечности частоты этих взаимодействий.
Все это и привело к возникновению во Вселенной гигантских газовых скоплений с полой топологической формой. Из ядер наиболее устойчивых газовых скоплений образовались квазары. Из-за больших как случайных, так и автоволновых флуктуаций термодинамических характеристик вещества и антивещества внутри квазаров имело место довольно значительное радиальное мигрирование их срединной сингулярной поверхности. Это вместе с неравенством нулю скорости света на этой сингулярной поверхности и являлось причиной интенсивного протекания аннигиляции вещества и антивещества а, следовательно, причиной и сверхвысокой светимости квазаров. Процесс образования сверхновых из полых звезд также сопровождается аннигиляцией вещества и антивещества. Этим и объясняется кратковременная чрезвычайно высокая светимость таких сверхновых.
Абсолютная устойчивость вещества обусловлена наличием явления убегания удаленных объектов от наблюдателя (расширения Вселенной). Абсолютная устойчивость антивещества, наоборот, обусловлена наличием явления набегания удаленных объектов на наблюдателя. Поэтому, расширение Вселенной принципиально никогда не может перейти в ее сжатие. Оно является бесконечно долгим эволюционным процессом. Этот процесс, как и само непрерывное существование вещества во Вселенной, обусловлен непрерывным калибровочным изменением свойств физического вакуума (старением физического вакуума).
Список литературы
Эйнштейн А. Сущность теории относительности. М.: ИЛ, 1953.
Иваненко Д.Д. Актуальность теории гравитации Эйнштейна. В кн. Проблемы физики: классика и современность. Ред. Тредер Г.-Ю., М.: Мир, 1982, с. 127.
Мёллер К. Успехи и ограниченность эйнштейновской теории относительности и гравитации. В кн.: Астрофизика, кванты и теория относительности. Ред.: Федоров Ф.И., М.: Мир, 1982, с. 17.
Мёллер К. Неизбежны ли сингулярности в теории гравитации? В кн.: Проблемы физики: классика и современность. Ред. Тредер Г.-Ю., М.: Мир, 1982, с. 99.
Хокинг С. Интегралы по траекториям. В кн.: Общая теория относительности. Ред.: ХокингС., ИзраэльВ., М.: Мир, 1983, с. 363.
Hawking S., Penrose R. Proc. Roy. Soc., 1970, v. A314, p. 529.
Хокинг С., Эллис Дж. Крупномасштабная структура пространства-времени, М.: Мир, 1977.
Weyl H. Phys. Z., 1923, b. 24, s. 230.
Weyl H. Philos. Mag., 1930, v. 9, p. 936.
Мёллер К. Теория относительности. М.: Атомиздат, 1975.
Утияма Р. К чему пришла физика? (От теории относительности к теории калибровочных полей), М.: Знание, 1986.
Дирак П.А.М. Космология и гравитационная постоянная. В кн. Воспоминания о необычайной эпохе. М: Наука, 1990, с. 178.
Горелик Г.Е. История релятивистской космологии и совпадение больших чисел. В кн. Эйнштейновский сборник. 1982...1983. Ред. Кобзарев И.Ю., М.: Наука, 1986, с. 302.
Lemaitre G.J. Math. and Phys., 1925, v, 4, p. 188.
Robertson H.P. Philos. Mag., 1928, v. 5, p. 839.
Даныльченко П.И. Псевдоинерциально сжимающиеся системы отсчёта координат и времени. В сб. Калибровочно-эволюционная теория Мироздания, Винница, 1994, вып. 1, с. 22.
Даныльченко П.И. Основы калибровочно-эволюционной теории Мироздания (пространства, времени, тяготения и расширения Вселенной). – Винница, 1994. – 78 с.
Калибровочно- эволюционная интерпретация специальной и общей теорий относительности. Киев, НиТ, 2005.
Даныльченко П.И. Природа релятивистского сокращения длины. В сб. Калибровочно-эволюционная интерпретация специальной и общей теорий относительности, Вінниця, О. Власюк, 2004, с. 3.
Релятивистское сокращение длины и гравитационные волны. Сверхсветовая скорость распространения. Киев, НиТ, 2005.
Даныльченко П.И. Калибровочные основы специальной теории относительности. В сб. Калибровочно-эволюционная интерпретация специальной и общей теорий относительности, Вінниця, О. Власюк, 2004, с.7.
Калибровочная интерпретация СТО. Киев, НиТ, 2005.
Пенроуз Р. Конформная трактовка бесконечности. В кн.: Гравитация и топология. Актуальные проблемы. Ред.: Д. Иваненко. – М.: Мир, 1966. – с. 152.
Bondi H. Cosmology. Cambridge, 2nd Ed., 1960, p. 38, 45.
Линде А.Д. Физика элементарных частиц и инфляционная космология. М.: Наука, 1990.
Weyl H. Raum-Zeit-Materie, 3rd edn. 1920; 5th edn. – Berlin 1923; Space, Time and Matter. – Methuen, London, 1922.
Пуанкаре А. Наука и гипотеза. В кн. О науке. М.: Наука, 1983, с. 5.
Сойер У. Вселенная Пуанкаре. В кн. Прелюдия к математике. М.: Просвещение, 1972, с. 72.
Мостепаненко А. Пространство и время в макро-, мега- и микромире. М.: Политиздат, 1974.
Riess A. et al. Type Ia Supernova Discoveries at z>1 From the Hubble Space Telescope: Evidence for Past Deceleration and Constraints on Dark Energy Evolution, Astrophysical Journal, 2004, v. 607. – P. 665...687.
Fuller R.W., Wheeler J.A. Phis. Rev., 1962, v. 128, p. 919.
Уилер Дж. Гравитация как геометрия (II). В кн. Гравитация и относительность. Ред. Цзю Х., Гоффман В., М.: Мир, 1965, с. 141.
Лоскутов А.Ю., Михайлов А.С. Введение в синергетику. М.: Наука, 1990.
Winfree A.T., Strogatz S.H. Physica, 1983, v. 9D, p. 35.
Winfree A.T., Strogatz S.H. Physica, 1983, v. 9D, p. 65.
Winfree A.T., Strogatz S.H. Physica, 1983, v. 9D, p. 333.
Winfree A.T., Strogatz S.H. Physica, 1983, v. 13D, p. 221.
Уиллер Дж. Принцип Маха как граничное условие для уравнений Эйнштейна. В кн. Гравитация и относительность. Ред. Цзю Х., Гофман В., М.: Мир, 1965, с. 468.
Salam A. Gauge interactions, elementarity and superunification. Preprint IC/81/9, Intern. Theor. Phys.,Trieste, 1981; Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, v. 304, Is. 1982, p. 135.
Clifford W.K. Lectures and Essays, Stephen L., Pollock F., eds., Macmillan, London, 1879, p. 244, 322.
Clifford W.K. Mathematical Papers, R. Tucker, ed., Macmillan, London, 1882, p. 21.
Мизнер Ч., Торн К., Уиллер Дж. Гравитация. Бишкек: Айнштайн, 1997, т. 3, с. 469.
Wheeler J.A. Geometrodynamics, Academic Press, New York, 1962.
Бор Н., Химия и квантовая теория строения атома. Избр. науч. тр., М.: Наука, 1971, т. 2, с. 75.
Горелик Г.Е. Судьба гипотезы Н. Бора о несохранении энергии. В сб. Нильс Бор и наука XX века, Киев: Наукова думка, 1988, с. 83.
Эйнштейн А., Подольский Б., Розен Н. Можно ли считать, что квантовомеханическое описание физической реальности является полным?, УФН, 1936, т. 16, вып. 4.
Вижье Ж.-П. Доклад о парадоксе Эйнштейна – Подольского – Розена. В кн. Проблемы физики: классика и современность. Ред. Г.-Ю., М.: Мир, 1982, с. 227.
Гейзенберг В. Физика и философия. М., 1963, с. 133...134.
Зельманов А.Л. Многообразие материального мира и проблема бесконечности Вселенной. Вкн. БесконечностьиВселенная. М.: Мысль, 1969, с. 274...324.
Menger K. The Theory of Relativity and Geometry, in: Albert Einstein: Philosopher-Scientist, p. 474.
Даныльченко П. Нежесткие системы отсчёта координат и времени, сжимающиеся в пространстве Минковского. В сб. Калибровочно-эволюционная теория Мироздания, Винница, 1994, вып. 1, с. 52.
Широков Ю.М. Доклады АН СССР, 1956, III, с. 1123.
29-04-2015, 03:10
