(76)
Проинтегрируем (76) по координате х
от 0
до s
с учетом условия короткого замыкания электродов: V
= 0 или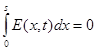 
Тогда получим выражение для плотности тока в виде:
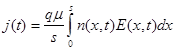(77)
Для расчета тока релаксации необходимо в любой момент времени знать распределения концентрации свободных носителей заряда и электрического поля в пленке. Видно, что в условиях короткозамкнутой цепи ток уже не равен нулю, как было в случае релаксации за счет собственной проводимости.
Задача о переносе неравновесных носителей заряда в электрете для решения требует учета кинетики освобождения носителей с ловушек и и их повторного захвата (рис. 33).
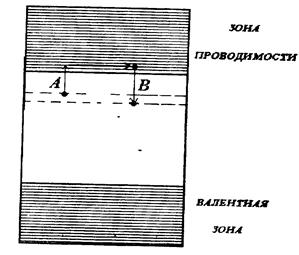
Рис 33 Явления делокализации и повторного захвата неравновесного носителя заряда на энергетической диаграмме. А -делокализация (освобождение) носителя с ловушки в зону проводимости, В - повторный захват
За счет теплового движения происходят акты освобождения некоторых носителей с уровня ловушки, при которых они переходит в зону проводимости и могут двигаться в электрическом поле электрета. Наоборот, свободные и движущиеся в электрическом поле носители, встретив ловушку, могут быть захвачены ею. Акты освобождения и захвата происходят многократно, пока носитель движется сквозь толщу диэлектрика. Подвижность носителя зависит от таких процессов захвата
Изменения концентраций свободных М захваченных на ловушки носителей описывается кинетическими уравнениями:
(78)
(79)
где 
- частота освобождения носителей из ловушек, ω0t т.н. эффективный частотный фактор, τt- время повторного захвата носителя на ловушку, τf - время пролета носителем расстояния до электрода
Рассмотрим приближенное решение для случая, когда исходное распределение заряда имеет форму «ступеньки», причем а существенно меньше s. В начальные периоды релаксации форма «ступеньки» не успевает заметным образом исказиться. Кроме того, допустим, что процесс освобождения носителей с ловушек идет медленно, так что п(х, t) <<n t(х, t). В этом случае внутреннее электрическое поле электрета будет практически полностью определяться захваченным на ловушки зарядом.
Запишем уравнение Максвелла для напряженности электрического поля divD = ρ , которое в нашем одномерном случае примет вид:
(80)
где q[п(х, t)+п t(х, t)]=ρ(х, t) - плотность заряда в пленке. Умножим обе части на Е(х, t) и μ, поделим на s и придем к выражению;
(81)
Проинтегрируем его по x от 0 до s:
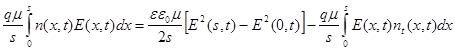
На основании выражения (77) можно записать:
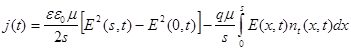.(82)
Воспользуемся . выражением для напряженности электрического поля в пленке (34) для случая прямо-прямоугольного распределения. Подставляя его в первое слагаемое (82), делая элементарные вычисления и преобразования, приходим к выражению:
(83)
Вычислим интеграл в (82) с учетом (34);
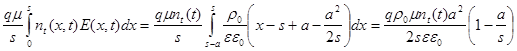(84)
где принято во внимание, что при х< s-а n t(х, t)=0 и подынтегральное выражение равно нулю, а при s- a≤ x≤ s концентрация захваченного на ловушки заряда п t(х, t)≡п t( t) не зависит от координаты.
Тогда для плотности тока ТСР получим выражение:
(85)
Осталось определить временные зависимости концентраций захваченного и свободного зарядов. Величину а мы полагаем постоянной, так как рассматриваем начальные моменты релаксации, когда край ступеньки не успевает сместиться. Это можно сделать с помощью кинетических уравнений (78) и (79) в т.н. квазистационарном приближении , когда
а)
и 
б)
(глубокие ловушки - времяповторного захвата намного превышает время пролета носителем расстояния до ближайшего электрода)
Тогда в системе уравнений (78) и (79) получим:
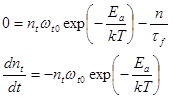(86)
Заменим переменную (время на температуру). Тогда из первого уравнения (86) получим:
(87)
Интегрируя второе, найдем температурную зависимость концентрации захваченного заряда:
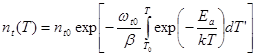(88)
Оценим «время» пролета носителем расстояния до ближайшего (х=s) электрода. Носитель, освободившийся из ловушки, дрейфует в соответствии с направлением электрического поля. Рассмотрим рис. 17. Если х>x0, носитель пойдет к ближайшему электроду х==s, а при х<
x0 -
к электроду х=0.
Причем во втором случае, преодолевая большую толщину диэлектрика, он наверняка захватится ловушкой, не достигнув электрода. Поэтому время «пролета» целесообразно оценивать для носителей, движущихся к ближайшему электроду х=s. Расстояние Δх, которое необходимо преодолеть такому носителю, равно s-x0.
С учетом (35), 
так как 
. Тогда:
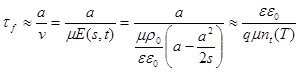(89)
где учтено, что n<< nt и a<< s. Подставим полученное выражение в (87):
(90)
Подставим (90) и (88) в (85):
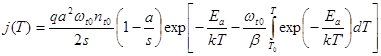(91)
Данное выражение и дает решение задачи о токе ТСР, связанном с движением неравновесных носителей заряда в собственном электрическом поле. Оно аналогично полученным ранее выражениям тока ТСД или ТСР с точностью до коэффициентов, не зависящих от температуры. Точно так же на графике тока ТСР будет наблюдаться максимум, а начальный участок дает возможность применять метод Гарлика-Гибсона для определения энергии активации ловушек в материале. Последнее справедливо только для образцов, в которых имеется один сорт ловушек - с одним значением энергии активации. При наличии распределения ловушек по энергиям или даже дискретного набора энергий активации пики на кривых ТСР будут размытыми, а применение метода начального подъема недопустимым.
Заметим, что данное приближенное решение имеет в основном учебное значение, иллюстрируя физические принципы ТСР. Оно почти не дает полезной информации о реальных процессах в диэлектрике. Ведь в процессе релаксации меняется форма пространственных распределений захваченного и свободного неравновесного зарядов, напряженности электрического поля. Для определения формы этих распределений в любой момент времени и точного расчета тока ТСР прибегают к численному интегрированию дифференциальных уравнений переноса заряда при заданных начальных и граничных условиях.
Задача сводитсяк численному решению уравнений Максвелла:
непрерывности
и кинетического
Граничные условия учитывают наличие (отсутствие) короткозамкнутой цепи, характер прилегающих к диэлектрику электродов, наличие инжеции носителей из электродов и др. факторы.
Используемая литература:
1. Беляев И.П., Дружинин В.П., Рожков И.Н. Электретный эффект
2. Бартенев Г.М.,Зеленев Ю.В. Физика и механика полимеров
3. Губкин А.Н. Электреты
4. Электреты / Под редакцией Г.Сесслера
29-04-2015, 02:08