Структуризация и систематизация сюжетных задач по сложности их решения

Н.Г. Рыженко, Н.А. Жигачева, Омский государственный педагогический университет, кафедра методики преподавания математики

Анализ школьной практики показывает, что формирование умения у учащихся вести поиск решения сюжетных задач, организация стратегии и тактики этого поиска учителем невозможна без выявления структуры решения задачи - основных ее частей (структурных элементов) и отношений между ними. Предварительно напомним определение некоторых используемых понятий [1, 2].

Определение 1. Отношением R на множестве M называется подмножество R множества MxM = M2.

Пусть M = {0; 2; 5; 7}, тогда M2 = {0;0; 0;2; 0;5; 0;7; 2;0; 2;2;2;5; 2;7; 5;0; 5;2; 5;5; 5;7; 7;0; 7;2; 7;5; 7;7}.

Из множества M2 выделим подмножество R тех пар  x;y, в которых xy. Выпишем эти пары: {2;0; 5;0; 5;2; 7;0; 7;2; 7;5}. Если x; y R, то "х находится в отношении R с у" или xRy. Само выражение xRy называется соотношением.

Определение 2. Отношение R на множестве M называется отношением строгого порядка (или строгим порядком), если оно антирефлексивно и транзитивно. Множество M с заданным на нем отношением строгого порядка R, т.е. пару M; R, называют упорядоченным множеством. Наглядно отношение строгого порядка можно представить в виде модели.

Определение 3. Моделью называется кортеж M; R1, R2, ..., Rm , где M - некоторое множество, а R1, R2,..., Rm - отношения на этом множестве (не обязательно бинарные).

В педагогических исследованиях широкое применение получили модели, в которых в качестве структуры объекта исследования выступает граф.

Определение 4. Графом Г называется непустое множество M и множество отношений, заданных на M [2].

Граф (рис.1) является моделью бинарного отношения R. Круги, соответствующие числам, - вершины графа; ориентированные отрезки, соединяющие вершины - ребра графа (дуги). Это модель M;с одним (бинарным) отношением строгого порядка.

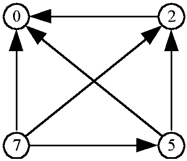
Рис. 1

Рассмотрим специальный класс отношений строгого порядка - так называемые древесные порядки. Пусть имеется множество M с отношением строгого порядка . Элемент x0 называется наибольшим, если для всякого у  M, отличного от x0, выполнено соотношение уx0. Очевидно, что наибольший элемент, если он существует, единствен.

Определение 5. Отношение строгого порядка на множестве M называется отношением древесного порядка (или древесным порядком), если

1) из того, что xу и xz следует, что у и z сравнимы;

2) во множестве М, , существует наибольший элемент.

Множество M с заданным на нем древесным порядком называют деревом, а наибольший элемент - корнем дерева. Для конечного дерева существует числовая характеристика - сложность дерева, которую будем отождествлять со сложностью решения задачи.

На рис.2 изображены деревья, имеющие одинаковое число вершин, и показан способ нахождения сложности дерева ((Дi)).

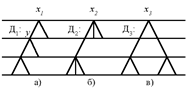
Рис. 2

Так, например, сложность вершины (x1) = 2·7, где 2 - число ребер, входящих в x1; 7 - число всех вершин, включая и саму вершину x1. Аналогично - (у) = 2·5 и т.д. Суммарная сложность всех вершин и дает сложность дерева Дi:

(Д1) = 2·7+2·5 + 2·3 = 30, соответственно

(Д2) = 3·7+3·4 = 33,

(Д3) = 2·7+2·3+2·3 = 26 [1, c. 141-142].

Заметим, что граф с бинарным отношением строгого порядка можно "расслоить" в дерево.

Проводя семантический анализ сюжетных задач, Л. М. Фридман [3] выделил следующие виды отношений, связывающих величины и их значения: отношение соединения; отношение отнимания; отношение сравнения (если величина задана двумя своими значениями): разностное отношение или кратное отношение двух значений величины, отношение разбиения (разделения); отношение-зависимость. Эти отношения являются уже не бинарными, а тернарными.

Будем рассматривать задачу как систему, т.е. как множество элементов, находящихся в определенном отношении друг к другу, причем это отношение обладает определенным свойством [4]. При построении моделей систем нужно учитывать то важное обстоятельство, что будучи аналогом системы модель не может достигнуть степени сложности оригинала. В модели стремятся отразить какое-нибудь одно отношение или структуру, специально выделенную для исследования. Поэтому моделирование по своей логической структуре напоминает умозаключение по аналогии. Вывод по аналогии о некоторых свойствах модели может быть экстраполирован на оригинал (систему) только в том случае, если отношения между элементами модели и системы установлены по одним и тем же свойствам и понимаются в одном и том же смысле. Эти отношения являются внутренними [4]. Отношение между величинами в задаче (отношение равенства) может быть установлено по разным свойствам:

a·b = c - по мультипликативным свойствам;

a+b = с - по аддитивным свойствам.

В дереве дуги задают бинарное отношение между вершинами. В задаче же отношение между величинами является тернарным, и устанавливается оно по разным свойствам. Поэтому будем рассматривать дерево, в котором фиксируется свойство, по которому установлено тернарное отношение равенства и называть его дерево-оператор (в дальнейшем просто дерево).

Моделирование сюжетных задач с помощью дерева рассмотрим на примере структурирования простейших задач. Структурирование - мыслительная деятельность по установлению отношений между величинами задачи. Для этого, используя восходящий анализ, построим граф - поиск решения задачи [5].

Задача I.1. Скорость велосипедиста 15 км/ч. Какое расстояние он проедет за 2 часа?

В задаче рассматривается одна ситуация - равномерное движение велосипедиста, характеризующееся тремя взаимосвязанными величинами: скорость движения V, время движения t и пройденный путь S. Эти величины связаны между собой формулой S = V·t. Если отвлечься от конкретного содержания задачи, то, обозначив первую величину через a, вторую - через b и третью - через c, получим зависимость между этими величинами: a·b = c.

Если рассматривать задачу как систему, то элементами ее решения будут значения величин (среди них два структурных элемента - известны, а одно значение - путь, является искомым); между величинами установлено тернарное отношение равенства по мультипликативному свойству. Ясно, что отношение является внутренним.

Итак, есть множество, состоящее из трех величин, между значениями этих величин установлено отношение равенства, следовательно, есть все формальные предпосылки для построения модели решения задачи в виде дерева (рис. 3):

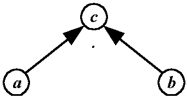
Рис. 3

c = a·b. В силу обратимости операций умножения и деления можно найти a = c/b или b = c/a.

Моделью решения сюжетной задачи является дерево. Оно характеризует структуру решения сюжетной задачи и сложность решения, отождествляемую со сложностью дерева:  = 2·3 = 6. Структурными элементами решения задачи являются вершины дерева.

Задача I.2. Из двух пунктов навстречу друг другу выехали два велосипедиста. Найти их скорость сближения, если скорость первого 15 км/ч, а скорость второго 13 км/ч.

В задаче задана одна величина a - скорость и три ее значения, из которых два известны, и одно искомое - скорость сближения. Дерево (рис. 4а) характеризует отношение сложения : a = a1+a2. В силу обратимости операций сложения и вычитания можно найти a1 = a-a2 или a2 = a-a1. Сложность решения задачи:  = 2·3 = 6.

Структурными элементами решения задачи являются три значения величины.

Поскольку в одной и той же задаче могут быть как отношение соединения, так и отношение отнимания, то для этих отношений целесообразно рассмотреть два дерева (рис. 4а и 4б).

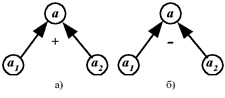
Рис. 4

Задача I.3. Скорость первого велосипедиста 12 км/ч, а скорость второго на 3 км/ч больше. Какова скорость второго велосипедиста?

Величина, рассматриваемая в задаче, - скорость задана двумя значениями: скорость первого велосипедиста a1 = 12 км/ч и скорость второго велосипедиста a2 - искомое значение. Имеющееся же в условии задачи данное: "на 3 км/ч больше" - не является значением рассматриваемой величины, а есть размер разностного сравнения заданных двух значений величины - скорости.

Дерево характеризует отношение разностного сравнения: a2 = a1+3 (рис. 5). Сложность решения задачи:  = 2·3 = 6. Структурными элементами решения задачи являются два значения одной величины и размер разностного сравнения.

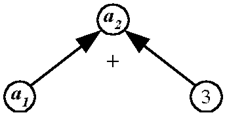
Рис. 5

Задача I.4. Скорость велосипедиста 15 км/ч, а скорость мотоциклиста в 3 раза больше. Найти скорость мотоциклиста.

В задаче I.4 задано отношение кратного сравнения двух значений величины - скорости. Дерево (рис. 6) и характеризует это отношение: a2 = 3а1. Сложность решения задачи:  = 2·3 = 6.

Структурные элементы решения задачи: два значения величины (скорости) : a1 = 15 км/ч - известное, a2 - искомое, 3 - размер кратного сравнения скоростей.

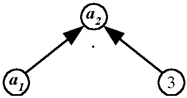
Рис. 6

Задача 2. Велосипедист, двигаясь со скоростью 12 км/ч, проехал 24 км. Какое расстояние пройдет за это время мотоциклист, скорость которого 36 км/ч?

Величины, рассматриваемые в задаче: скорость, время и расстояние. Расстояние задано двумя значениями, одно из них - искомое, скорость также имеет два значения: a1 = 12 км/ч, a2 = 36 км/ч. Значение величины времени одинаково как для велосипедиста, так и для мотоциклиста. В задаче рассматриваются две ситуации: равномерные движения велосипедиста и мотоциклиста, заданные отношением c = а·b, причем структурный элемент b является общим для обеих ситуаций (рис.7).

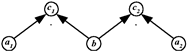
Рис. 7

Этот граф не является деревом, но его можно "расслоить" в лес (совокупность деревьев), каждое из которых описывает одну ситуацию (рис.8).

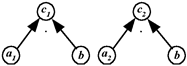
Рис. 8

Сложность леса в дальнейшем будем характеризовать как суммарную сложность деревьев, его составляющих:

 = (c1)+(c2) = 6+6 = 12; 1) c1 = a1·b, b = c1/a1; 2) c2 = a2·b, c2 = a2·c1/a1.

Назовем деревья I.1 - I.4 деревьями I порядка сложности. Систематизацию задач в систему (систематизация - мыслительная деятельность по установлению более удаленных отношений) рассмотрим на примерах получения деревьев более высоких порядков сложности.

Задача 3. Скорость мотоциклиста на 20 км/ч больше скорости велосипедиста. Найти скорость велосипедиста, если известно, что расстояние между двумя пунктами, равное 96 км, мотоциклист проезжает за 3 часа.

Моделью структуры решения задачи является дерево. В модели два отношения: отношение зависимости и отношение разностного сравнения (рис.9):

с км - расстояние между пунктами; a2 км/ч - скорость мотоциклиста; a1 км/ч - скорость велосипедиста; b ч - время. 1) c = a2·b, 2) a2 = a1+20, 3) c = (a1+20)·b, a1 = (c-20b)/b.  = 2·5+2·3 = 16.

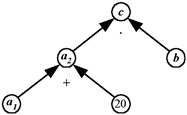
Рис. 9

Задача 4. Из двух пунктов, расстояние между которыми 96 км, одновременно навстречу друг другу выехали велосипедист и мотоциклист и встретились через 2 ч. Найти их скорости, если скорость мотоциклиста в три раза больше, чем скорость велосипедиста.

Модель решения задачи приведена на рис.10.

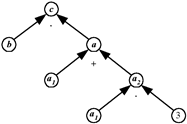
Рис. 10

c, км - расстояние; b, ч - время; a1, км/ч - скорость велосипедиста; а2, км/ч - скорость мотоциклиста; 3 - размер кратного сравнения; а, км/ч - скорость сближения. 1. c = a·b; 2. a = a1+a2; 3. a2 = 3a1; 4. c = (a1+3a1)·b: c = 4a1·b; a1 = c/4b, a2 = 3c/4b;  = 2·7 + 2·5 + 2·3 = 30.

Мы привели только несколько примеров выявления структур решения задач и определения сложности их решения с помощью деревьев. Эти примеры позволяют сделать следующие выводы.

Если рассматривать задачу как сложную систему, то:

1. Моделью решения задачи является дерево.

2. Структура решения задачи - это соответствующее ей дерево или лес, которые строятся из деревьев I порядка.

3. Структурные элементы решения задачи - вершины дерева: значения величин, как известные, так и неизвестные, среди них и искомые; числа, которые задают размер кратного или разностного сравнения между двумя значениями одной величины.

4. Дерево I порядка описывает простейшие отношения между величинами: отношения-зависимости, отношения соединения (отнимания), отношения разностного или кратного сравнения.

5. Отношения, характерные для дерева I порядка, являются внутренними, так как они зависят только от самих соотносящихся объектов (значений величин).

6. В деревьях более высоких порядков реализуется несколько внутренних отношений.

7. Структура решения задачи - объективная ее характеристика, которая позволяет дать количественную оценку, являющуюся основой для систематизации задач в систему по нарастающей сложности их решения. Структурный анализ решения задач в учебниках VII класса показал, что наибольшая сложность решения  = 152, а наибольшее число задач приходится на сложность  = 32.

Список литературы

Шрейдер Ю.А. Равенство, сходство, порядок. М.: Наука, 1971.

Березина Л.Ю. Графы и их применение. М., 1979.

Фридман Л.М. Логико психологический анализ школьных учебных задач. М., 1977.

Уемов А.И. Системы и системные исследования // Проблемы методологии системного исследования. М., 1970.

Крупич В. И. Структура и логика процесса обучения математике в средней школе: Метод. разработки по спецкурсу для слушателей ФПК. - М., 1985.