Непрерывная ректификация

1. ЛИТЕРАТУРНЫЙ ОБЗОР

1.1. Теоретические основы разрабатываемого процесса

1.1.1. Общие сведения о процессе ректификация

Ректификация представляет собой процесс многократного частичного испарения жидкости и конденсации паров. Процесс осуществляется путем контакта потоков пара и жидкости, имеющих различную температуру, и проводится обычно в колонных аппаратах. При каждом контакте из жидкости испаряется преимущественно легколетучий, или низкокипящий, компонент (НК), которым обогащаются пары, а из паров конденсируется преимущественно труднолетучий, или высококипящий, компонент (ВК), переходящий в жидкость. Такой двухсторонний обмен компонентами, повторяемый многократно, позволяет получить в конечном счете пары, представляющие собой почти чистый НК. Эти пары после конденсации в отдельном аппарате образуют дистиллят (ректификат) и флегму – жидкость, возвращаемую для орошения колонны и взаимодействия с поднимающимися парами. Пары получают путем частичного испарения снизу колонны остатка, являющегося почти чистым ВК.

Как отмечалось, достаточно высокая степень разделения однородных жидких смесей на компоненты может быть до­стигнута путем ректификации. Сущность процессов, из которых складывается ректификация, и получаемые при этом результаты можно проследить с помощью t — х — у -диаграммы (рис. 1.1).

Нагрев исходную смесь состава х₁ до температуры кипения получим находящийся в равновесии с жидкостью пар (точка b). Отбор и конден­сация этого пара дают жидкость состава x₂ обогащенную НК (х₂ > х₁).Нагрев эту жидкость до температуры кипения t₂, получим пар (точка d), конденсация которого дает жидкость с еще большим содержанием НК, имеющую состав х_а, и т. д. Проводя таким образом последовательно ряд процессов испарения жидкости и конденсации паров, можно получить в итоге жидкость (дистиллят), представляющую собой практически чи­стый НК.

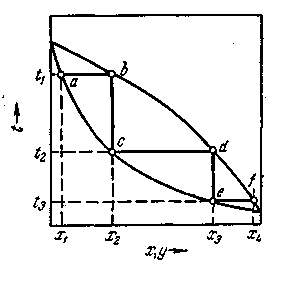
Рис. 1.1. Изображение процесса разделения бинар­ной смеси путем ректифика­ции на диаграмме t—Х—у.

Аналогично, исходя из паровой фазы, соответствующей составу жид­кости x₄, путем проведения ряда последовательных процессов конденса­ции и испарения можно получить жидкость (остаток), состоящую почти целиком из ВК.

В простейшем виде процесс многократного испарения можно осущест­вить в многоступенчатой установке, в первой ступени которой испаряется исходная смесь. На вторую ступень поступает на испарение жидкость, оставшаяся после отделения паров в первой ступени, в третьей ступени испаряется жидкость, поступившая из второй ступени (после отбора из последней паров) и т. д. Аналогично может быть организован процесс многократной конденсации, при котором на каждую следующую ступень поступают для конденсации пары, остав­шиеся после отделения от них жидкости (конденсата) в предыдущей ступени.

При достаточно большом числе ступеней таким путем можно получить жидкую или паровую фазу с достаточно высокой концен­трацией компонента, которым она обогаща­ется. Однако выход этой фазы будет мал по отношению к ее количеству в исходной смеси. Кроме того, описанные установки отличают­ся громоздкостью и большими потерями теп­ла в окружающую среду.

Значительно более экономичное, полное и четкое разделение смесей на компоненты достигается в процессах ректификации, про­водимых обычно в более компактных ап­паратах — ректификационных колоннах.

Процесс ректификации осуществляется путем многократного контакта между неравновесными жидкой и паровой фазами, движущимися относи­тельно друг друга.

При взаимодействии фаз между ними происходит массо- и теплообмен, обусловленные стремлением системы к состоянию равновесия. В резуль­тате каждого контакта компоненты перераспределяются между фазами: пар несколько обогащается НК, а жидкость — ВК. Многократное контактирование приводит к практически полному разделению исходной смеси.

Таким образом, отсутствие равновесия (и соответственно наличие раз­ности температур фаз) при движении фаз с определенной относительной скоростью и многократном их контактировании являются необходимыми условиями проведения ректификации.

1.1.2. Равновесие в системах жидкость-пар

В общем случае жидкая смесь может состоять из нескольких компонентов. В простейшем случае из двух, например из компо­нентов А и В. Характер поведения жидкой смеси зависит главным образом от природы составляющих ее веществ и давления.

Для идеальных растворов характерно то, что сила взаимодейст­вия между всеми молекулами (одноименными и разноименными) равна. При этом общая сила, с которой молекула удерживается в смеси, не зависит от состава смеси. Очевидно, что парциальное давление в этом случае должно зависеть лишь от числа молекул, достигающих в единицу времени поверхности жидкости со ско­ростью, необходимой для преодоления сил внутреннего притяжения молекул, т. е. при данной температуре давление соответствующего компонента возрастает пропорционально его содержанию в жидкой смеси (закон Рауля):

р_А = Р_Ах_А (1.1) и р_В = Р_В(1-х_А) (1.2.)

Закон Рауля справедлив и для газов с температурой ниже критической (т. е. такой температуры, выше которой газ при увели­чении давления не сжижается).

По степени растворимости компонентов смеси жидкости подраз­деляют на взаиморастворимые в любых соотношениях, частично растворимые и практически взаимонерастворимые. В свою очередь смеси со взаиморастворимыми компонентами в любых соотноше­ниях делятся на: идеальные растворы, которые подчиняются закону Рауля; так называемые нормальные растворы - жидкие смеси, частично отклоняющиеся от закона Рауля, но не образующие смесей: с постоянной температурой кипения (азеотропов); неидеальные растворы - жидкости со значительными отклонениями от закона Рауля, в том числе смеси с постоянной температурой кипения (азеотропы). (Отметим, что полностью взаимонерастворимых жидкостей нет, обычно все жидкости хотя бы в незначительных количествах, но растворяются друг в друге. Однако в этих случаях на практике для удобства принимают такие жидкости взаимонерастворимыми.)

Смесь двух жидкостей, взаиморастворимых в любых соотноше­ниях, представляет собой систему, состоящую из двух фаз и двух компонентов, и по правилу фаз:

С=К-Ф+2=2-2+2=2 (1.3.)

имеет две степени свободы (из трех - давления Р, температуры t, концентрации х). Однако при анализе и расчете процессов перегонки жидкостей одну из переменных обычно закрепляют и строят диа­грамму фаз в плоской системе координат. При этом возможны следующие варианты фазовых диаграмм: Р — t (х = const), Р — — x(t = const), t — х(Р = const).

Для технических расчетов наиболее важной является диаграмма t — х, у, так как обычно процессы перегонки в промышленных аппаратах протекают при Р = const, т. е. в изобарных условиях. На этой диаграмме (рис. 5.2.) по оси абсцисс отложены концентрации жидкой х и паровой у фаз, отвечающие различным температурам.

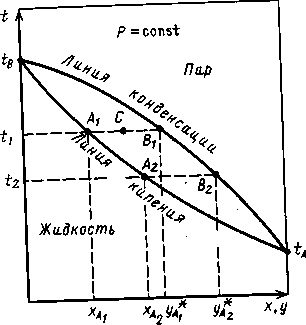
Рис. 1.2. Фазовая диаграмма t — х, у

По закону Дальтона р_А = Рy^*_A, и тогда

y^*_A= p_A/P=(P_A/P) x_A, (1.4.)

но

Р = p_A+p_B=P_Ax_A+P_B(1-x_B)=P_B+(P_A-P_B)x_A (1.5.)

тогда

x_A=(P-P_B)/(P_A-P_B) (1.6.)

По уравнению (1.6.)) по известным Р_А и Р_B при заданной температуре t₁ , t₂ и т.д. находят х_A , х_B и т.д., а затем по уравнению (1.4.) -соответствующие значения у*_A1 , у*_А2 и т.д. и по найденным точкам строят линии кипения жидкости (кривая t_AA₂A₁t_B) и конденсации паров (кривая t_AB₂B_lt_B). Отметим, что уравнение (1.6.) устанавливает связь между концентрациями (по жидкости) и заданными давлениями (общим Р и насыщенных паров Р_А и Р_B). Отрезки А₁В₁ , А₂ В₂ и т. д., соединяющие точки равновес­ных составов жидкой и паровой фаз, являются изотермами.

Отметим, что точки, лежащие на кривой t_AA₂A₁t_B,, отвечают жидкой фазе, находящейся при температуре кипения. Очевидно, что любая точка, лежащая ниже этой кривой, характеризует систему, состоящую только из жидкой фазы. Аналогично, любая точка лежащая выше кривой t_A B₂ В₁ t_B , характеризует систему, темпера тура которой выше температуры начала конденсации пара, т. е пары в этой точке являются перегретыми, и система состоит только из паровой фазы. Точки, находящиеся между кривыми кипения и конденсации (например, точка С на рис. 1.2.), характеризуют системы, температуры которых выше температуры кипения жидко­сти данного состава и ниже температуры конденсации паров этого же состава. Таким образом, эти точки отвечают равновесным парожидкостным системам.

Основные положения фазового равновесия были рассмотрены в гл. 2 (правило фаз Гиббса, законы Генри и Рауля и др.). Там же для идеальных бинарных систем получено уравнение (1.7.), которое описывает линию равновесия:

у*_А = ах_А/[1+х_А(а-1)], (1.7.)

где а = Р_А/Р_В - относительная летучесть компонента А (иногда а называют коэффи­циентом разделения).

Очевидно, что для смеси, состоящей из n компонентов, например, А, В, С, D, на основе законов Рауля и Дальтона имеем

y_A = (Р_A/Р)х_A; y_B = (Р_B/Р)х_B; y_C = (Р_C/Р)х_C; y_D = (Р_D/Р)х_D. (1.8.)

Поскольку

P=P_Ax_A+ P_Bx_B+ P_Cx_C+ P_Dx_D+ …=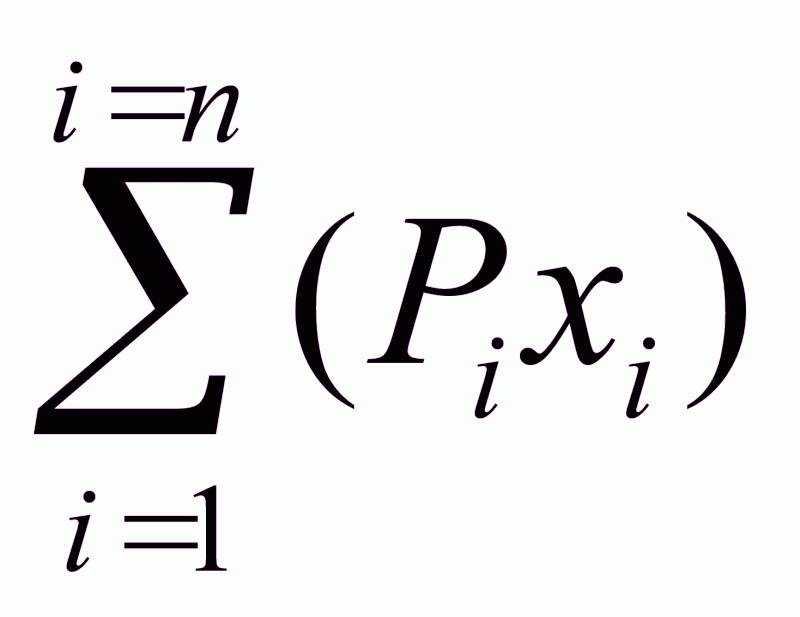 (1.9.)

то для любого j-го компонента

y_j = P_jX_j/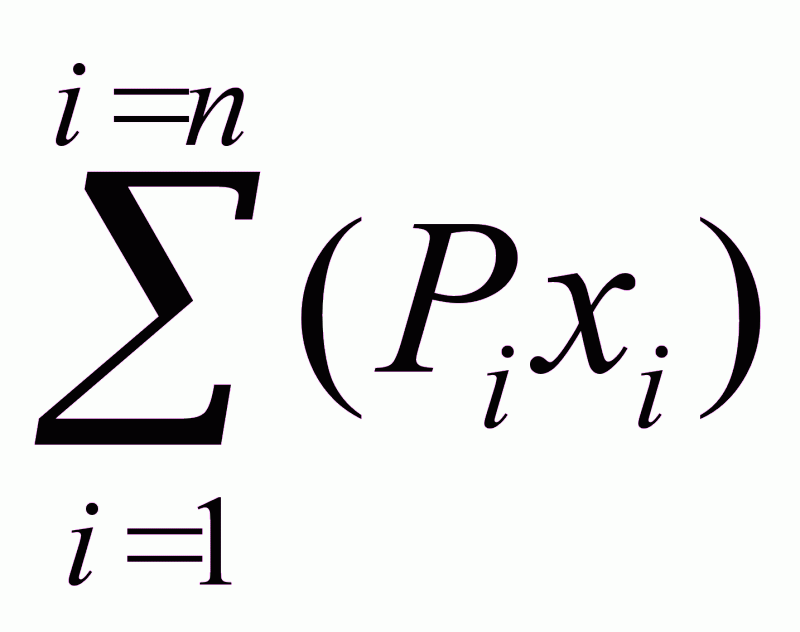. (1.10.)

Разделив числитель и знаменатель правой части уравнения (1.10) на величину Р_А, получим

y_j = а _jX_j/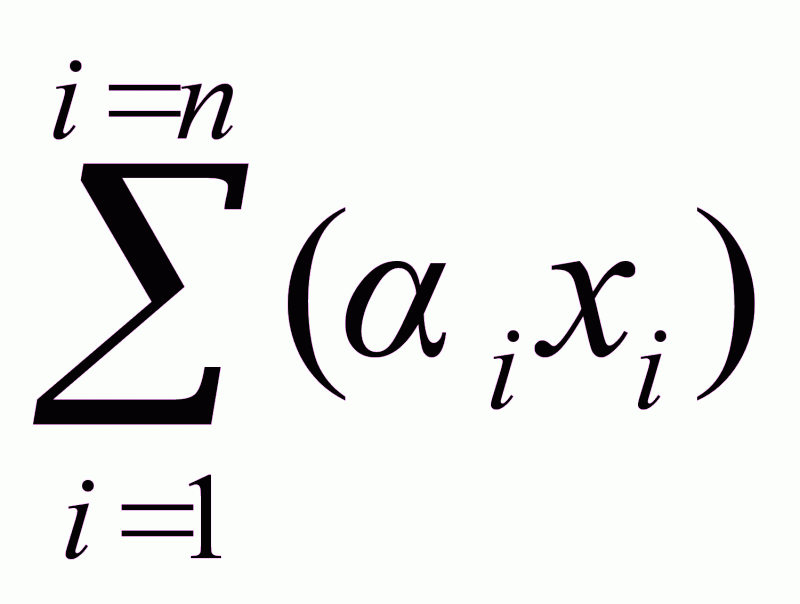, (1.11.)

где а _A = Р_А/Р_В ; а _в = Р_В/Р_А ; а _C = Р_С/Р_А и т. д.

Например, зависимость давления насыщенного пара от темпера­туры хорошо описывается эмпирическим уравнением Антуана

lnР_А = А - В/(Т+ C), (1.12.)

где А - постоянная, не зависящая от температуры; В и С -константы, определяемые по справочникам; T- абсолютная температура.

Уравнение (5.12) описывает температурную зависимость давле­ний паров в интервале температур до нескольких десятков градусов и при давлениях, не слишком близких к критическим.

Взаимное положение кривых на фазовых диаграммах t — х — у и у — х как для идеальных, так и для реальных систем могут быть определены с помощью законов Коновалова. Законы Коновалова устанавливают связи между изменениями состава, давления или температуры в двухфазных системах, они лежат в основе теории перегонки и ректификации бинарных смесей.

Первый - закон Коновалова формулируется так: пар обогащается тем компонентом, при добавлении которого к жидкости повышает­ся давление пара над ней или снижается ее температура кипения, или пар всегда более обогащен НК, чем соответствующая ему равновесная жидкая фаза.

Первый закон Коновалова дополняется первым правилом Врев­ского, отражающим влияние температуры на равновесные составы фаз: при повышении температуры бинарной смеси в парах возрас­тает относительное содержание того компонента, парциальная молярная теплота испарения которого больше.

Это можно проиллюстрировать с помощью фазовой диаграммы (рис. 1.2.). Для идеальной смеси очевидно, что при одной и той же температуре t содержание НК в парах у*_A1 (точка B₁ больше его содержания х_а в равновесной с парами жидкости (точка А₁). При добавлении к смеси НК ее температура кипения снижается, но содержание НК в паре остается выше, чем в жидкости.

Реальные жидкие смеси могут значительно отклоняться от закона Рауля. Если зависимость полного давления (или сумма парциальных давлений) паров от состава жидкой смеси проходит выше линий, характеризующих те же зависимости для идеальных смесей (рис. 1.3.), то такое отклонение называют положительным, если ниже - отрицательным отклонением от закона Рауля. Эти отклонения определяются изменением активности молекул в раст­воре, диссоциацией, гидратацией и др. Степень отклонения реаль­ной системы от закона Рауля выражают величиной коэффициента активности :

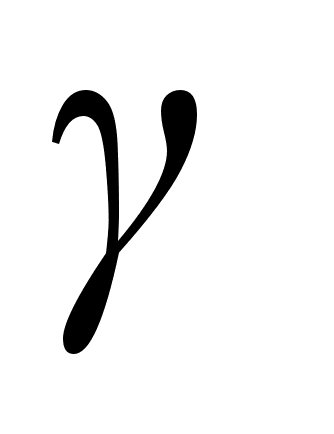p_A = P_Ax_A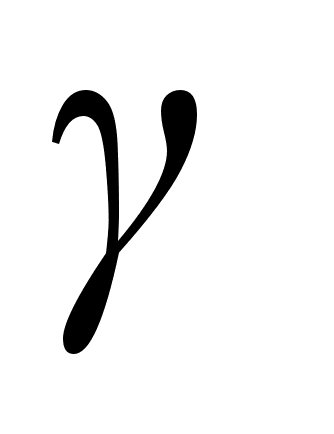 . (1.13.)

Для смесей с положительным отклонением от закона Рауля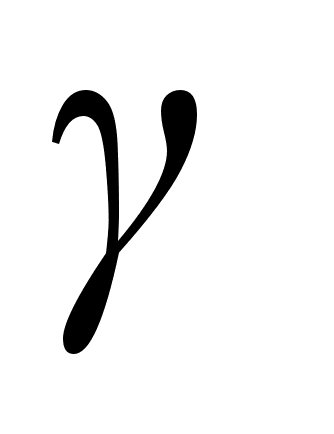
> 1, для смесей с отрицательным отклонением — 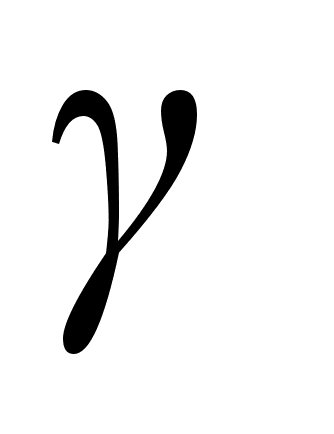< 1. Отметим, что определение значений у часто затруднительно, поэтому диа­граммы P — х обычно строят по экспериментальным (справочным) данным.

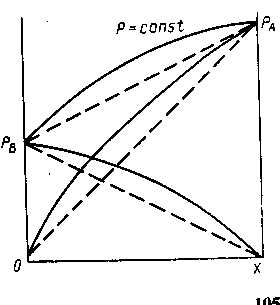
Рис. 1.3. Диаграмма р — х для смеси с поло­жительным отклонением от закона Рауля (пунктиром показаны соответствующие ли­нии для идеального раствора)

Для многих реальных смесей от­клонение от закона Рауля настолько существенно, что приводит к качест­венно новому состоянию системы, а на фазовых диаграммах Р — х и t — х появляются (рис. 1.4.,б, в) от­носительный максимум или мини­мум. При этом кривые жидкости и пара соприкасаются друг с другом в экстремальных точках, в которых составы равновесных фаз одинаковы. Такие смеси, как известно, называют азеотропными, или азеотропами. Их основная особенность состоит в том, что при испарении такая смесь (азеотроп) не изменяет своего состава, поэтому для ее разделения требуются специальные методы (азеотропная и экстрактивная рек­тификация, изменение давления и др.).

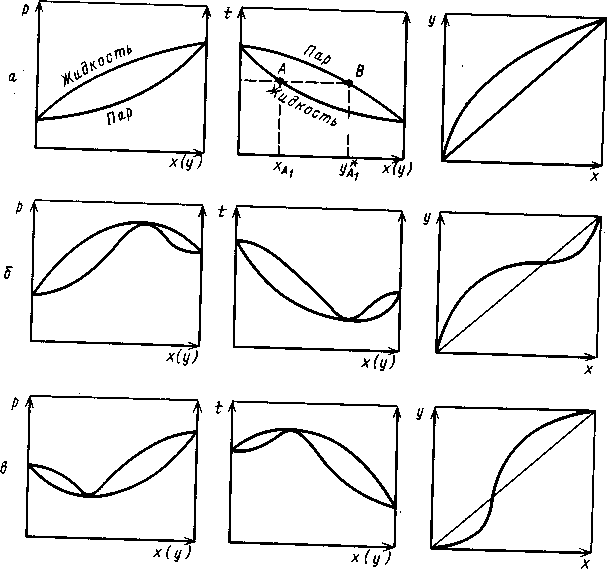
Рис. 1.4. Фазовые диаграммы равновесия жидкость-пар для идеальной (а) и реаль- ных (б, в) систем

Эта особенность азеотропных смесей постулируется вторым законом Коновалова, который можно сформулировать следующим образом: если давление и температура сосуществования двух бинар­ных фаз имеют экстремум (максимум или минимум), то составы фаз одинаковы. Это справедливо для фаз любой природы. Для систем жидкость - пар второй закон Коновалова определяет основ­ное свойство азеотропов.

При изменении внешних условий - температуры (или давления) значение а изменяется различно по разные стороны от точки азеотропа; одна часть «рыбки» (рис.1.4., б, в) должна становиться шире, другая - уже. Очевидно, что в части диаграммы, где в паре содержится больше, чем в растворе, компонента с меньшей теплотой испарения, при понижении температуры (давления), а увеличи­вается.

5.1.3. Материальный и тепловой балансы ректификационной колонны

Пусть, согласно схеме на рис. (1.5.), в колонну поступает F кмоль исходной смеси, состав которой х_F мол. долей НК. Сверху из колонны удаляется G кмоль паров, образующих после конденсации флегму и ди­стиллят. Количество получаемого дистил­лята Р кмоль, его состав х_P мол. долей НК. На орошение колонны возвращается флегма в количестве Ф кмоль, причем ее состав равен составу дистиллята (х_ф= x_P мол. долей). Снизу из колонны удаля­ется W кмоль остатка состава x_w мол. до­лей НК.

Тогда уравнение материального баланса колоны будет:

Ф+F = G+W. (1.14)

Поскольку G=P+Ф, то

F = P+W. (1.15.)

Соответственно по НК материальный баланс:

Fx_F = Px_P+Wx_W (1.16.)

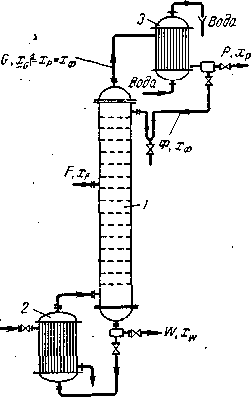
Рис. 1.5. К составлению материального баланса ректи­фикационной колонны:

/ — колонна; 2 — куб; 3 — дефлег­матор.

Для колонны непрерывного действия с учетом потерь тепла в окружающую среду имеем:

Приход тепла Расход тепла

С теплоносителем в кипя- С парами, поступающими из

тальнике .……… Q_КИП.. колонны в дефлегматор Q_G = GI

С исходной смесью……….Q_F=Fi_F С остатком………………… Q_W =Wi_w

С флегмой ................. . Q_Ф = Фi_Ф Потери в окружающую среду Q_П

Кроме известных величин, в выражения для количеств тепла входят: I, i_F, i_ф и i_w — энтальпии соответственно паров, выходящих из колон­ны, исходной смеси, флегмы и остатка.

Таким образом, уравнение теплового баланса:

Qкип + Q_F + Q_Ф = Q_G + Q_W + Q_{П .} (1.17.)

Подставляя вместо Q их значения и учитывая, что F=Р + W, G = P(R+ 1) и Ф = PR, получим

Qкип + (Р + W)i_F + РRi_Ф = P(R+)I + Wi_W + Q_П (1.18.)

Решая уравнение (5.18.) относительно Qкип, находим расход тепла в кипятильнике

Qкип = Р(I – i_F) + PR( I -i_Ф) + W(i_W - i_F) + Q_П ( 1.18а. )

Из уравнения теплового баланса (5.18а.) видно, что тепло, подво­димое в кипятильник, затрачивается на испарение дистиллята [Р(I—i_F)], испарение флегмы [PR(I — i_ф)], нагревание остатка до температуры ки­пения [W(i_w — i_F)], а также на компенсацию потерь тепла в окружаю­щую среду.

Флегма из дефлегматора поступает в колонну при температуре ее ки­пения. Поэтому энтальпия выходящих из колонны паров I == i_Ф + r_ф, где r_ф — теплота испарения флегмы.

Потери тепла в окружающую среду обычно выражают в долях тепла, подводимого в кипятильник, т. е. принимают Q_П = a_ПQ_кип, где при нали­чии хорошей тепловой изоляции коэффи­циент а_П = 0,03—0,05.

Делая соответствующие подстановки в уравнение (1.18а.), окончательно получим

Q_КИП =[P(I – i_F) + PRr_Ф + W(i_W - i_F)] / (1-a_П) (1.19.)

Энтальпии жидкостей, входящих в урав­нение (1.18.) и (1.19.), равны произве­дениям их мольных теплоемкостей с на тем­пературы t (в °С). Теплоемкости с и теплоты испарения для бинарных смесей вычисляют по правилу аддитивности исходя из свойств чистых компонентов А и В:

с = с_Ах+с_В(1—х)

r = r_Ах+r_В(1—х)

где х — мольная доля компонента А в смеси.

Количество тепла Q_ДЕФ, отнимаемого ох­лаждающей водой в дефлегматоре, зависит от количества конденсирующихся в нем паров. При полной конденсации паров, выходящих из колонны, находим

Q_ДЕФ = P(R+1)r_Ф = P(R+1)(I-i_Ф) (1.20.)

Уравнения рабочих линий. Для получе­ния уравнений рабочих линий воспользуем­ся общим для всех массообменных про­цессов уравнением ():

y=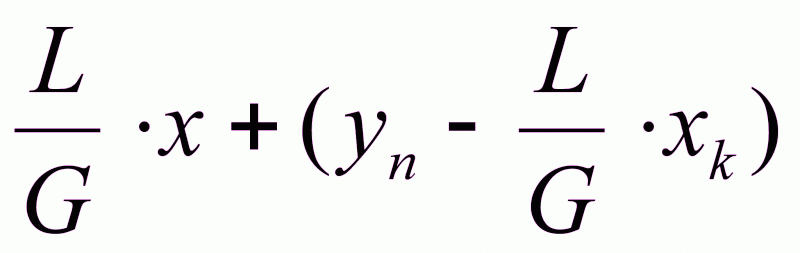, (1.21)

где L и G — расходы жидкой и паровой фаз; у, х, у_а и х_к —соответственно текущие концентрации паровой и жидкой фаз и их концентрации на верхнем конце колонны .

Применяя это уравнение к процессу ректификации, выразим все вхо­дящие в него величины в мольных единицах.

Укрепляющая часть колонны. Количество жидкости (флегмы), стекаю­щей по этой части колонны

L = Ф = PR, (1.22)

где R=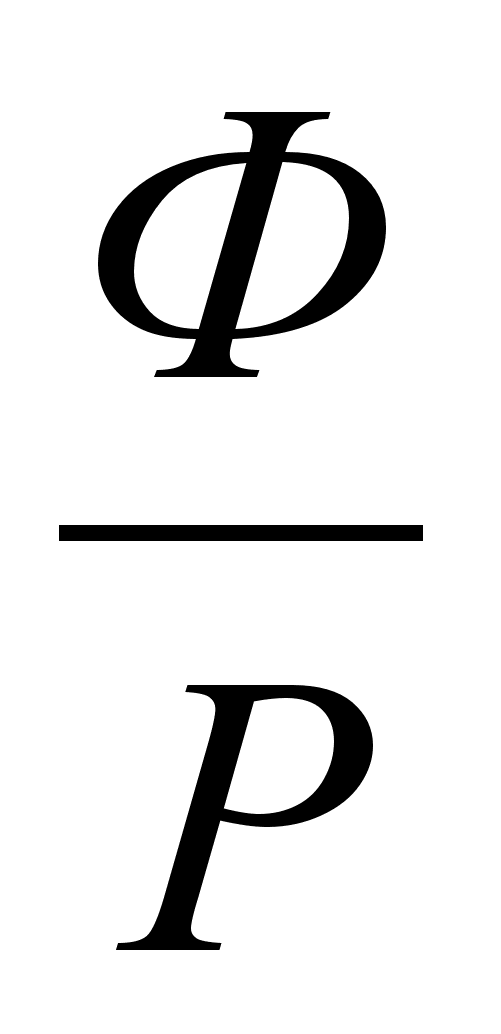 -флегмовое число, представляющее собой отношение количества флегмы к количеству дистиллята.

Количество паров, поднимающихся по колонне

G=P+Ф=P+PR=P(R+1), (1.23)

Для верхнего конца укрепляющей части колонны состав паров y_G=y_P и, согласно принятому выше допущению, у_р = х_р. Следовательно, в данном случае у_н = х_р.

В том же сечении колонны состав жидкости (флегмы), поступающей из дефлегматора, x_ф = х_р, т. е. х_к = х_р. Учитывая значения L, G, y_k и х_k получаем уравнение (1.24), получим

y=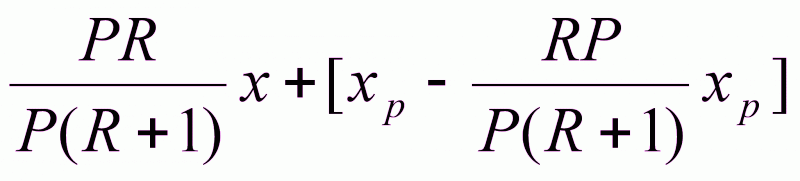 (1.24)


29-04-2015, 04:06