Логический анализ E-структур с помощью графов

Логический Анализ E-структур с помощью графов

Использование графов и у-множеств при логическом выводе в E-структурах позволяет не только упростить процесс получения следствий, но и выполнить другие методы логического анализа рассуждений.

Первое, что сделаем – это представим рассуждение в виде ориентированного графа, в котором отношения включения между множествами представлены как дуги, соединяющие соответствующие литералы. При этом будем считать, что дуги могут быть любой длины и необязательно прямыми. Рассмотрим посылки из условного примера:

1) CÍ;

2) TÍR;

3) Í.

Далее возьмем чистый лист бумаги и выпишем на некотором расстоянии друг от друга все базовые термины нашего рассуждения. При этом мы расположим термины в двух строках: в верхней строке будут все «позитивные» термины (C, S, T, R), а в нижней – все «негативные» термины (, , , ). Кроме того, альтернативные (т.е. отрицающие друг друга) термины (например, S и ) мы расположим строго на одной вертикали. Затем соединим некоторые термины дугами в соответствии с нашими посылками. Тогда получим ориентированный граф, с помощью которого изображается исходная задача (рисунок 1).

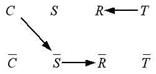
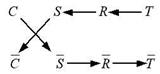
Рис. 1Рис. 2

Теперь для каждой посылки мы построим новую дугу, которая будет изображать следствие, полученное с помощью правила контрапозиции. Наш граф дополнится еще тремя дугами (рисунок 2). Правила рисования контрапозиций для нашей схемы весьма просты и соответствуют некоторым принципам симметрии. Сформулируем эти правила:

1) если исходная дуга соединяет литералы в одной строке, то ее контрапозиция должна соединять противоположные литералы на другой строке, при этом дуга должна быть направлена в сторону, противоположную исходной дуге. Например, для дуги ® мы по этому правилу получаем новую дугу R®S;

2) если исходная дуга наклонная (т.е. соединяет разные строки), то при построении ее контрапозиции мы соединяем линией противоположные литералы (например, для дуги C® надо соединить линией литералы и S). После этого надо выбрать такое направление линии (вверх или вниз), чтобы это направление совпадало с направлением исходной дуги. Например, пара литералов на схеме соединяется дугой S®, так как в этом случае стрелка направлена вниз, так же как и исходная стрелка C® на схеме.

Дуги со строго вертикальным направлением в нашем примере не появятся. Забегая вперед, отметим, что такие дуги, если они появляются в процессе логического вывода, говорят о том, что в нашем рассуждении содержится коллизия парадокса.

Теперь, когда получены все следствия по правилу контрапозиции, можно приступать к получению новых следствий по правилу транзитивности. Если использовать схему, то этот процесс существенно упрощается. Для этого надо просто построить все пути, содержащиеся в полученном графе (рисунок 2). Сначала надо выбрать литералы, из которых будут строиться эти пути. Начинать нужно с минимальных литералов, т.е. с таких литералов на схеме, в которые не входит ни одна дуга. На схеме имеется два таких литерала: C и T. Построив пути из них, получим

Путь 1: C ®®®; Путь 2: T ® R ® S ®.

Выберем какую-либо произвольную вершину графа (например, R) и выделим те вершины графа, которые достижимы из R. Для нашего примера из вершины R достижимы вершины S и .

Теперь, если мы сопоставим понятие достижимости с правилом транзитивности в наших правилах вывода, то придем к следующему правилу, позволяющему получать на наших схемах новые следствия:

Если на схеме вершина Z достижима из вершины Y, то связь Y®Z является либо исходной посылкой, либо следствием нашего рассуждения, полученном по правилу транзитивности.

Посмотрев теперь на рисунок 2, нетрудно убедиться, что все следствия C4 – C9 могут быть также получены с помощью правила достижимости. Еще проще эти следствия можно получить, если выписать в одной строчке каждый из путей. Тогда транзитивные связи и соответственно следствия полученные по правилу транзитивности можно получить, если нарисовать все возможные стрелки, направление которых совпадает с общим направлением пути (рис. 3). На этом рисунке для наглядности исходные посылки обозначены жирными стрелками. Все остальные стрелки обозначают следствия.

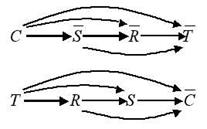
Рис. 3

Получение сразу всех возможных следствий из посылок уже вносит некоторый элемент новизны в традиционные системы логического вывода. В Аристотелевской силлогистике все правила предназначены для получения (или проверки) единственного заключения силлогизма (следствия) из двух посылок. Единственное заключение также получают при решении системы из большего числа посылок. Например, в системе Л. Кэрролла единственное заключение получается даже в том случае, если сорит состоит из 9-ти посылок.

Теперь познакомимся с еще одним основным понятием E‑структур. Мы будем рассматривать граф, который получится, если в граф исходной E-структуры добавить все возможные следствия. Пример такого графа показан на рисунке 3. Он играет важную роль в теории E-структур и в силу этого получил специальное название.

Определение 1. CT-замыканием E-структуры называется граф, в котором содержатся все посылки этой структуры и все ее следствия.

Происхождение названия этого графа связано с некоторыми известными понятиями современной математики. В частности, граф, который можно получить из исходного графа с помощью применения правила транзитивности, в теории графов называется транзитивным замыканием данного графа. Поскольку мы используем в E‑структурах при построении CT‑замыкания не только правило транзитивности (T), но и правило контрапозиции (C), то поневоле вынуждены внести некоторые изменения в традиционный термин.

Одним из важных свойств CT-замыкания является то, что оно выполняет роль инварианта для некоторого множества E-структур. Возможны E-структуры с одинаковой совокупностью терминов, но с разными исходными посылками, у которых, тем не менее, CT‑замыкания полностью совпадают. Это говорит о том, что данные E‑структуры логически эквивалентны. Кроме CT‑замыкания в E‑структурах имеются другие инварианты. С ними мы познакомимся позже.

При получении следствий из посылок мы используем свойства отношения включения множеств. Но это отношение является одним из отношений частичного порядка (см. предыдущий раздел). Поэтому мы можем при анализе E-структур использовать все свойства и методы анализа этого отношения.

Предположим, что нам заданы посылки, среди которых содержится некоторый термин, например, "укротители крокодилов", который мы обозначаем каким-либо литералом, например, T. Оказывается, можно не только поставить задачу вывода всех следствий из данных посылок, но и ответить на такой вопрос: "Какими качествами обладают укротители крокодилов?". Ответить на такой вопрос можно, если вывести все следствия по правилу контрапозиции и после этого построить верхний конус для данного литерала. Поскольку все литералы верхнего конуса данного литерала обозначают множества, в которые включено множество, соответствующее данному литералу, то, следовательно, все литералы верхнего конуса обозначают признаки (свойства), которые присущи данному литералу. Например, для задачи из примера 6 получим: T^D = {T, R, S, }. Отсюда, ясно, что укротители крокодилов в рамках заданного рассуждения имеют следующие свойства: они заслуживают уважения, разумны и не являются детьми.

Для закрепления полученных знаний полезно решить самостоятельно еще одну задачу, взятую из книги Л. Кэрролла «История с узелками».

Даны посылки:

1) Все члены палаты общин находятся в здравом рассудке.

2) Все, кто носит титул пэра, никогда не принимают участия в скачках на мулах.

3) Все члены палаты лордов носят титул пэра.

Что из этого следует? Какими свойствами обладают те, кто принимает участи в скачках на мулах?

Указание: рекомендуется ограничить универсум только членами парламента и учесть, что парламент состоит только из двух палат (это, в частности означает, что множество членов палаты лордов является дополнением множества членов палаты общин).

При разработке и реализации алгоритмов и программ анализа рассуждений используется не наглядное изображение E‑структуры, а ее представление в виде некоторых соответствий. Эти соответствия состоят из множества пар, в которых первым элементом является литерал, а вторым элементом – множество литералов. Например, пары (, {A, C}) и (C, Æ) могут быть элементами такого соответствия. Число таких пар в каждом соответствии равно числу литералов в структуре. Одним из таких часто используемых соответствий является соответствие "Верхние конусы", которое содержит множество пар типа(литерал, верхний конус этого литерала).

Еще одним возможным соответствием является "CT-замыкание". Оно состоит из множества пар вида(литерал, множество литералов, достижимых из этого литерала).

В математике и логике инвариантом системы принято считать некоторое свойство, остающееся неизменным при выполнении определенных преобразований в системе. Для E‑структур примем в качестве такого преобразования построение ее CT-замыкания, т.е. добавление к исходным посылкам всех возможных полученных с помощью правил вывода следствий.

Оказывается, что к одному и тому же CT-замыканию нередко приводятся разные на первый взгляд системы исходных посылок. В то же время может оказаться, что некоторые незначительно отличающиеся друг от друга системы посылок имеют принципиально отличающиеся CT-замыкания. Все это позволяет считать CT-замыкание некоторой обобщающей характеристикой (логическим инвариантом) рассуждения, заданного E‑структурами.

Предположим, что E-структура R задана своими исходными посылками. Выделим какую-либо из этих посылок (например, A®B) и представим, что вместо нее в E-структуру R введена в качестве посылки ее контрапозиция (т.е. посылка ®). В этом случае суждение A®B будет уже не исходной посылкой R, а ее следствием, но в CT-замыкании структуры R обе эти посылки будут присутствовать и в первом, и во втором случае. При этом окажется, что и все CT-замыкание E-структуры R при такой замене останется неизменным.

Вполне возможна также ситуация, когда в исходных посылках E-структуры присутствует посылка, которая является следствием каких-то других ее посылок. В процессе вывода мы эту посылку получим, но она тут же будет изъята, так как при выводе мы обязательно проверяем новизну следствий и оставляем только те суждения, которых до этого не было в наличии. И опять же CT-замыкание таких, на первый взгляд разных, структур будет одним и тем же. И если в первой структуре имеются коллизии, то эти коллизии сохранятся, если мы вместо некоторых посылок введем их контрапозиции или добавим в посылки суждения, которые являются следствиями этих посылок.

Таким образом, если нас интересуют в E-структуре не следствия из ее исходных посылок, а вся структура в целом с коллизиями или без оных, то мы можем считать инвариантом E-структуры ее CT‑замыкание.

Возьмем в качестве примера сорит Кэрролла.

Все опытные люди компетентны;

Дженкинс всегда допускает грубые ошибки в работе;

Все компетентные люди не допускают грубых ошибок в работе.

Сделаем в нем следующие изменения:

1) первую и третью посылки заменим на их контрапозиции;

2) добавим во вторую посылку одно из следствий данной структуры;

3) изменим порядок посылок.

Тогда мы можем получить, например, такую последовательность исходных посылок:

Дженкинс некомпетентен и всегда допускает грубые ошибки в работе;

Каждый, кто допускает грубые ошибки в работе, некомпетентен;

Все некомпетентные люди неопытны.

Ясно, что посылки здесь отличаются, и следствия соответственно будут другими. К тому же в первой посылке не один, а два предиката суждения. Но если мы, используя одни и те же обозначения терминов, построим для каждого из этих случаев CT-замыкание и сравним их, то мы увидим, что они совпадают.

Отметим одну особенность E-структур. В них результат вывода не зависит от того, в каком порядке введены или перечислены исходные посылки. Этим они отличаются от Аристотелевых силлогизмов, в которых тип силлогизма, а во многих случаях и его результат зависит от порядка перечисления исходных посылок. Для E‑структур порядок ввода посылок становится существенным в тех случаях, когда появляются какие-либо коллизии. Тогда имеет смысл выделить из всего множества посылок такой E-структуры наиболее сомнительные и вначале исследовать систему без этих посылок. А потом уже на основании полученных результатов корректировать сомнительные посылки. Еще один вариант управления порядком ввода посылок мы рассмотрим в разделе о неполных рассуждениях.

В качестве упражнения рассмотрим две E-структуры E₁ и E₂ , заданные исходными посылками:

E₁ : X®(Y, ); Y®; Z®;

E₂ : X®Y; Z®(,); V®(,).

Определите с помощью построения и сравнения CT-замыканий этих структур, являются ли они инвариантными.

Существует, оказывается, еще один и к тому же во многих отношениях более удобный инвариант E-структур. Посмотрим внимательно на рисунок 3. На нем изображено CT-замыкание задачи из примера 6, представленное в виде направленных в одну сторону (слева направо) путей. Обратите внимание, что некоторые дуги соединяют литералы, между которыми имеется другой более длинный путь. Дуги, обладающие таким свойством, представляют следствия, полученные с помощью правила транзитивности. Если убрать из рисунка все такие дуги, то мы получим простые пути типа C®®®и T®R®S®, из которых можно восстановить все CT-замыкание, используя при этом в качестве правила вывода только правило транзитивности.

Пути такого типа называются в упорядоченных структурах максимальными путями. В произвольных E-структурах их может быть больше двух, они могут самым причудливым образом пересекаться друг с другом, но все они обладают двумя главными свойствами:

1) из совокупности этих путей можно полностью восстановить CT-замыкание E-структуры, используя только правило транзитивности, и

2) ни одна связь в этих путях не может быть получена из других связей с помощью правила транзитивности.

Определение 2. Диаграммой Хассе E-структуры называется граф, содержащий только связи, включенные в максимальные пути и не содержащий никаких связей, полученных по правилу транзитивности. Диаграмма Хассе E-структуры является ее инвариантом.

Таким образом, мы можем любую E-структуру представить не только с помощью CT‑замыкания, но и с помощью диаграммы Хассе. При этом структура становится более наглядной. Попробуем оценить, сколько лишних связей мы используем, если представляем ее в виде CT-замыкания. Для простоты представим, что наша E-структура содержит два максимальных пути, и каждый из этих путей содержит N базовых терминов. Тогда общее число связей в диаграмме Хассе этой структуры равно 2(N-1). В CT-замыкании той же самой структуры будет содержаться уже N(N-1) связей. Определим, сколько связей будет «сэкономлено» при использовании диаграммы Хассе. Обозначим число таких "лишних" связей буквой K. Тогда

K = N(N-1) -2(N-1) = -3N + 2.

Выражение -3N + 2 является полиномом второй степени от N. Это означает, что при увеличении числа N количество «сэкономленных» связей K возрастает в квадратичной зависимости. Так, при N = 4 число связей в диаграмме Хассе и в CT‑замыкании будет равно соответственно 6 и 12, но если N = 10, то соотношение будет уже другим: 18 и 90. Разница и соответственно «экономия» будут уже существенными.

У диаграммы Хассе имеется еще одно интересное свойство, которое можно практически использовать при анализе E-структур и соответственно при анализе моделируемых с их помощью рассуждений. Это свойство определяется следующей теоремой. Пусть имеется некоторая E-структура G, заданная определенными суждениями (посылками). Граф структуры G, который получается после применения правила контрапозиции (правила C) ко всем посылкам обозначим G^C , а диаграмму Хассе этой структуры (если мы ее каким-то способом сумели построить) – G^H . Тогда соблюдается следующее соотношение:

Теорема 1. Для любых E-структур соблюдается G^H ÍG^C .

Это означает, что после того, как будут построены контрапозиции исходных посылок, в полученном графе будут в наличии все дуги диаграммы Хассе. Хотя не исключено, что при этом в графе будут присутствовать и лишние для диаграммы Хассе дуги, которые мы можем легко распознать и удалить.

Но наша «экономия» лишних связей на этом не заканчивается. Можно, оказывается, любую E-структуру представить числом связей, в два раза меньшим, чем число связей в диаграмме Хассе. Обратите внимание, что в диаграмме Хассе все связи «ходят парами»: суждение и его контрапозиция. А почему бы нам каждую такую пару не представить всего одним суждением? Ведь все равно изъятое суждение мы получим, применив к оставшемуся суждению правило контрапозиции.

Этот инвариант, составленный из половины суждений диаграммы Хассе, назван минимальным множеством посылок E-структуры. Почему минимальным? А потому что исходная E-структура может содержать посылки, которые на самом деле логически следуют из остальных посылок. Если эту E-структуру дополнить всеми следствиями, получаемыми с помощью правила C, а потом преобразовать полученную систему в диаграмму Хассе, то мы, сравнивая исходные посылки с суждениями диаграммы Хассе, сможем найти «лишние» (т.е. выведенные из других посылок)


10-09-2015, 21:00