 ГОСУДАРСТВЕННЫЙ КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННЫЙ КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ПО ВЫСШЕМУ ОБРАЗОВАНИЮ
Новочеркасский государственный технический университет
ПЕТРОВ ИГОРЬ АЛЬБЕРТОВИЧ,
ассистент каф. СМ, СиПМ НГТУ,
соискатель кафедры “Сопротивление
материалов, строительная и
прикладная механика”.
| Моделирование как необходимый научный метод познания и его связь с детерминированными и стохастическими методами ИЗУЧЕНИЯ ЛЮБОГО явления или процесса |
Р Е Ф Е Р А Т
Реферат представлен для сдачи кандидатского экзамена по философии.
Научный руководитель
Зарифьян Александр Захарович,
профессор, д-р техн. наук,
зав. каф. “Сопротивление материалов, строительная и прикладная механика”.
Руководитель по кафедре философии
Ефимов Владимир Иванович,
доцент, канд. фил. наук.
Новочеркасск — 1996 г.
С О Д Е Р Ж А Н И Е
| ВВЕДЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 3 | |
| 1. | МОДЕЛИРОВАНИЕ КАК НЕОБХОДИМЫЙ ЭТАП ПОЗНАНИЯ СУЩНОСТИ ИЗУЧАЕМОГО ЯВЛЕНИЯ ИЛИ ПРО-ЦЕССА ПРИ РАЗРАБОТКЕ ЕГО ТЕОРИИ . . . . . . . . . . . . . . . . . . | 4 |
| 2. | ГИПОТЕЗЫ КАК НЕОБХОДИМЫЕ ПРИЗНАКИ, ОПРЕДЕ-ЛЯЮЩИЕ СВОЙСТВА РАЗРАБАТЫВАЕМОЙ МОДЕЛИ ИЛИ ПРОЦЕССА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 8 |
| 3. | ПРЕДСКАЗАНИЯ — ВАЖНЕЙШИЙ КРИТЕРИЙ ИСТИН-НОСТИ РАЗРАБАТЫВАЕМОЙ ТЕОРИИ . . . . . . . . . . . . . . . . . . . | 15 |
| 4. | ПРИМЕНЕНИЕ РАЗРАБОТАННОЙ ТЕОРИИ К ПРАКТИ-ЧЕСКИМ ЗАДАЧАМ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 16 |
| 5. | СВЯЗЬ МОДЕЛИРОВАНИЯ С ДЕТЕРМИНИРОВАННЫМИ И СТОХАСТИЧЕСКИМИ МЕТОДАМИ ИЗУЧЕНИЯ ЯВЛЕ-НИЯ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 17 |
| ЗАКЛЮЧЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 19 | |
| СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ . . . . . . . . . . . . . . . . . | 20 | |
В В Е Д Е Н И Е
Бурный рост промышленности и науки во всех сферах человеческой деятельности привели в настоящее время к такому положению вещей, что создание и разработка каких-либо новых технологий, технических средств (машин, приборов, оборудования и т. п.), а также методик их применения для нужд человека становится затруднительным, а в некоторых случаях невозможным, без интенсивного применения научных методов познания и поиска [2].
Одной из таких обязательных сторон научного исследования является метод моделирования, без которого не обходится ни одна конструкторская и ни одна исследовательская работа. По этой причине, в реферате сделан значительный акцент на метод моделирования как необходимый научный метод познания явлений природы и использование этого познания для практических целей [4].
1. МОДЕЛИРОВАНИЕ КАК НЕОБХОДИМЫЙ ЭТАП
ПОЗНАНИЯ СУЩНОСТИ ИЗУЧАЕМОГО ЯВЛЕНИЯ
ИЛИ ПРОЦЕССА ПРИ РАЗРАБОТКЕ ЕГО ТЕОРИИ
Всякое вновь изучаемое явление или процесс бесконечно сложно и многообразно и потому до конца принципиально не познаваемо и не изучаемо. Поэтому, приступая к изучению явления или процесса, исследователь заменяет его схематической моделью, которая выбирается тем более сложной, чем подробнее и точнее нужно изучить упомянутое явления. В моделе сохраняется только самые существенные стороны изучаемого явления, а все мало существенные свойства и закономерности отбрасываются [6].
Какие стороны изучаемого явления необходимо сохранить в модели и какие отбросить, зависит от постановки задачи исследований. Цель и задачи исследований формулируются перед началом разработки теории еще неизученного явления или уточнения уже существующей теории с целью более адекватного описания изучаемого процесса или явления [7]. Построение теории начинается с выбора некоторого достаточного множества понятий и определения тех объектов, с которыми будет оперировать формируемая теория. Иногда список исходно определяемых понятий и объектов называют терминами теории. Они должны быть определены так, чтобы воспринимались любым исследователем однозначно.
Далее необходимо ввести, при построении модели явления, самые необходимые свойства определяемых объектов (“кирпичей” теории) и правила их взаимодействия и преобразования. Список введенных свойств и правил должен быть полным, т. е. таким, оперируя с которым можно осуществить любое действие по решению поставленных в исследовании задач и доведения решения логического и однозначного результата. Указанный список должен быть логически непротиворечивым, иначе создаваемая теория приведет к ошибочным заключениям. Вводимые правила должны быть выполнимы, а результаты их использования однозначными и определенными.
Выделенное множество объектов-терминов теории и правил их преобразования должно допускать проверку практикой или иными надежными методами. При этом выбранная модель должна обеспечивать необходимую точность результатов [6].
В философском смысле дать определение некоторому понятию-термину — это значит подвести более узкое определяемое понятие или подпонятие под более широкого и указать отличительную особенность. Это означает, что, давая определения вводимым в теорию терминам, мы определяем их в конце концов через ряд неопределимых исходных понятий. Тем самым становится возможным неоднозначное толкование, которое позволяет прилагать сформулированную теорию к любым явлениям, имеющим в своей основе аналогичные структуры исходных понятий.
Так, например, в курсе геометрии в разделе планиметрия понятие точки не вводится, а понятие отрезок прямой o-b вводится как континуальное множество точек — последовательность точек c, ведущих из начальной точки отрезка o к конечной точке b, имеющее наименьшую длину

Рис. 1
Путем продолжения отрезка в направлении от точки d к с получаем полупрямую, а продолжая отрезок и в противоположную сторону от точки d, будем иметь бесконечную прямую(рис. 1).
В дальнейшем, точки рассматриваются как места пересечения линий.
Рассмотрим проективные модели Римана: проведем через точку o прямой перпендикуляр (рис. 2), на котором отметим точку o p , на отрезке o-o p , как на диаметре, построим окружность, касающуюся прямой в точке o. Точку o назовем полюсом.

Рис. 2
Соединим полюс с точками d, c и b, каждая из приведенных проектирующих прямых пересекает окружность в точках d ¢, c ¢ и b ¢. Очевидно, между точками d и d ¢, c и c ¢, b и b ¢, имеется взаимооднозначное соответствие. Полюс o p взаимооднозначно соответствует бесконечно удаленной точке прямой. Как видно в проективной модели Римана имеется образ одной бесконечно удаленной точки прямой — это точка, совпадающая с полюсом o p , в то время как на рис. 1 могло показаться, что прямая обладает двумя бесконечно удаленными точками. В развитие этой модели приведем проективную модель Римана для сферы и плоскости N.
Возьмем плоскость N, в точке o которой поместим сферу диаметром o-o p . Рассматривая точку o p как полюс проектирования, спроектируем
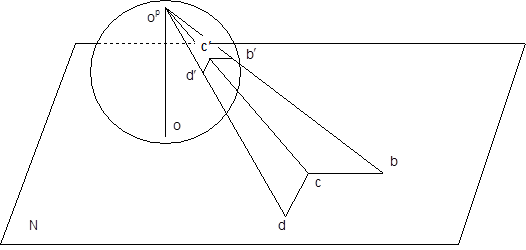
Рис. 3
прямыми, проходящими через полюс o p , расположенные в плоскости N, то точки d, c, b на поверхность сферы в виде точек-образов d ¢, c ¢, b ¢. Как и в линейном случае (рис. 2) между точками d, c, b и их проективными образами d ¢, c ¢, b ¢ имеется взаимно однозначное соответствие. Доказывается, что при таком проективном преобразовании сохраняются углы между линиями d, c, b на плоскости и линиями d ¢, c ¢, b ¢ на поверхности сферы. Рассмотренное проектированное преобразование служит теоретическим основанием для изображения карты земной поверхности на плоскости N и широко используется в навигации, в морском и авиационном штурманском деле. Полюс проектирования o p по Риману, также как и в линейном случае (рис. 2), является проективным образом бесконечно удаленной точки плоскости. Риманова модель дает основание считать, что плоскость содержит не множество бесконечно удаленных точек, а только одну. Такой подход дает большие удобства для математических построений в теории функции комплексного переменного и в прикладных задачах.
2. ГИПОТЕЗЫ КАК НЕОБХОДИМЫЕ ПРИЗНАКИ,
ОПРЕДЕЛЯЮЩИЕ СВОЙСТВА РАЗРАБАТЫВАЕМОЙ
МОДЕЛИ ИЛИ ПРОЦЕССА
Изучение всякого непознанного явления начинается с наблюдения его проявления в природе или в лаборатории. Сделанные наблюдения позволяют высказать ряд исходных предположений (гипотез), позволяющих объяснить на модели изучаемое явление и его свойства. Справедливость высказанных гипотез проверяется экспериментом. Подтвержденные экспериментом гипотезы путем логических рассуждений желательно оформленных в виде математического описания и построения превращаются в теорию исследуемого явления. При этом высвечиваются две стороны явления — качественное и количественное [1].
Таким образом, модель изучаемого явления с помощью вводимых гипотез приобретает ряд свойств, опираясь на которые можно путем математических и логических действий проследить, как принятая модель взаимодействует с окружающими объектами и, следовательно, как она реагирует на внешнее воздействие. При этом варианте возможно, что и первоначальное свойство модели изменится [5].
Проиллюстрируем роль вводимых гипотез на примерах.
Для хранения сжатого газа при высоких давлениях обычно применяются тонкостенные цилиндрические резервуары-баллоны, представляющие собой цилиндрическую оболочку вращения. Оболочка считается тонкостенной, если толщина стенки в 20-30 раз меньше диаметра баллона. Такая оболочка может рассчитываться по безмоментной теории, следовательно элемент стенки баллона работает только на растяжение-сжатие, таким образом гипотеза о малой толщине стенки сводится к тому, что изгибающими моментами, возникающими в стенке баллона можно пренебречь; в этом случае для определения действующих в оболочке нормальных напряжений можно пользоваться известным уравнением Лапласа (см. рис. 4)
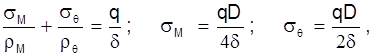
где ![]() ,
, ![]() — радиусы меридиана кольцевого сечения;
— радиусы меридиана кольцевого сечения;
![]() — давление газа;
— давление газа;
![]() — толщина стенки.
— толщина стенки.
Из этого уравнения выходит, что меридиональные нормальные напряжения sм в стенке баллона в 2 раза меньше тангенциальных (кольцевых) sq напряжений, следовательно разрушение баллона происходит в виде трещины, сориентированной вдоль образующей оболочки.
Для расчета толстостенной цилиндрической оболочки приходится применять моментную теорию, основанную на гипотезе, что и в стенке оболочки действуют наряду с нормальными напряжениями еще и поперечные силы и изгибающие моменты (рис. 5). Это уточненная модель приводит к совершенно иным уравнениям (дифференциальному уравнению четвертого порядка)
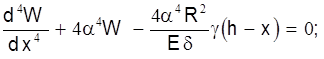
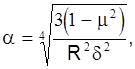
где W — перемещение элемента стенки резервуара в радиальном направлении;
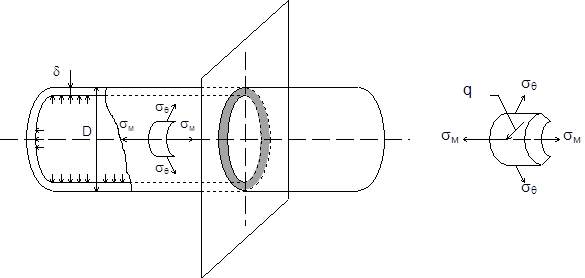
Рис. 4.
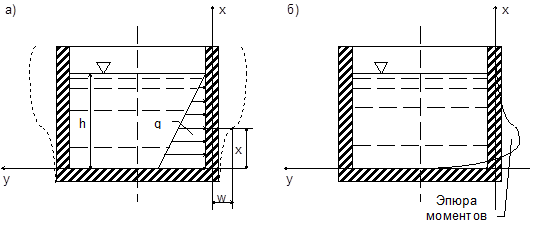
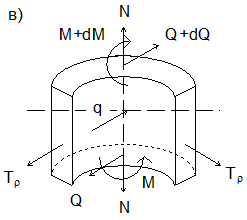
Рис. 5.
![]() — упругая постоянная стенки;
— упругая постоянная стенки;
![]() — модуль упругости материала;
— модуль упругости материала;
![]() — толщина стенки резервуара;
— толщина стенки резервуара;
![]() — удельный вес жидкости в резервуаре;
— удельный вес жидкости в резервуаре;
![]() — глубина жидкости в резервуаре;
— глубина жидкости в резервуаре;
![]() — коэффициент Пуассона.
— коэффициент Пуассона.
Изменение гипотезы привело к резкому усложнению модели и к более сложному алгоритму расчета оболочки на прочность.
Рассмотрим еще один пример из физики.
В классической механике Галилея-Ньютона при рассмотрении движения материального тела в пространстве вводятся, на первый взгляд, совершенно естественные гипотезы о том, что масса движущегося тела от скорости его движения не зависит, а время, отсчитываемое как в покоящейся, так и в движущейся инерционной системе отсчета, одинаково. При скоростях движения, близких к скорости света, такие гипотезы оказываются не верны и их приходится заменять гипотезами специальной теории относительности, предложенной Альбертом Эйнштейном. Специальная теория относительности представляет собой современную физическую теорию пространства и времени.
В специальной теории относительности, как и в классической Ньютоновской механике, предполагается, что время однородно, а пространство однородно и изотропно. В основе специальной теории относительности лежат две основные гипотезы, отличные от гипотез Галилея-Ньютона. Первая из них утверждает, что в любых инерциальных системах отсчета все физические явления при одних и тех же условиях протекают одинаково. Вторая гипотеза утверждает, что скорость света в вакууме не зависит от движения источника света. Она одинакова во всех направлениях и во всех инерциальных системах отсчета. Опыты показывают, что скорость света в вакууме — предельная скорость в природе. Скорость любых частиц, а также скорость любых взаимодействий сигналов не может превосходить скорость света c.
Объединение специальной теории относительности и классических представлений об абсолютном времени, идущем одинаково во всех системах отсчета, приводят к абсурду, что световой сигнал должен одновременно достигать точек пространства, принадлежащих двум различным сферам.
В специальной теории относительности ход времени в разных инерционных системах отсчета различен. Соответственно, промежуток времени между какими-либо двумя событиями относителен. Он измеряется при переходе от одной инерционной системы к другой. В частности, относительна одновременность двух событий, происходящих в разных точках пространства.
События, связанные причинно-следственной связью, не могут совершаться одновременно ни в одной системе отсчета, так как всякое следствие обусловлено каким-то процессом, вызываемым причиной. Между тем любой процесс (физический, химический, биологический) не может протекать мгновенно. Поэтому относительность ни в коей мере не противоречит причинности. В любой инерциальной системе отсчета события-следствия всегда совершаются позже, чем его причина.
Из гипотез специальной теории относительности, а также из однородности и изотропности пространства и однородности времени следует, что соотношение между координатами и временем одного и того же события в двух инерциальных системах отсчета выражаются преобразованиями Лоренца, а не преобразованиями Галилея, как это считается в классической Ньютоновской механике.
Преобразования Лоренца имеют простейший вид в случае, когда сходственные оси декартовых координат неподвижной и движущейся инерциальных систем попарно параллельны. Причем движущаяся система перемещается относительно неподвижной со скоростью вдоль оси OX. При этом преобразования Лоренца имеют вид
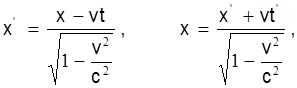

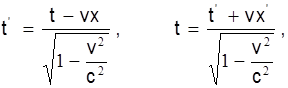
где c — скорость света в вакууме.
Преобразования Лоренца показывают, что при переходе от одной инерциальной системы отсчета изменяются не только пространственные координаты рассматриваемых событий, но и соответствующие им моменты времен. Из преобразования Лоренца следует, что скорость относительного движения любых инерциальных систем отсчета не может превосходить скорость света в вакууме.
Из преобразования Лоренца следует, что линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения. Это изменение продольного размера при движении называется Лоренцовым сокращением
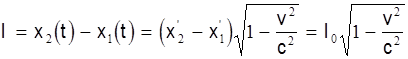 .
.
Поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета
Итак, линейные размеры тела относительны. Они максимальны в той системе отсчета, относительно которой тело покоится — эти размеры тела называются его собственными размерами
В релятивистской динамике, в отличие от классической, масса материальной точки не постоянна, а зависит от скорости этой точки. Зависимость массы от скорости выражается формулой
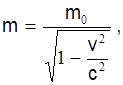
где m0 — масса покоя частиц.
В релятивистской механике делается важный вывод, что масса и энергия находятся в зависимости
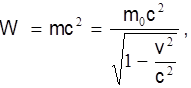
Приведенные примеры показывают, что простая замена исходных гипотез может приводить к серьезнейшим изменениям свойств модели явления.
3. ПРЕДСКАЗАНИЯ — ВАЖНЕЙШИЙ КРИТЕРИЙ
ИСТИННОСТИ РАЗРАБАТЫВАЕМОЙ ТЕОРИИ
После построения теории исследуемого явления делаются и анализируются важнейшие выводы, вытекающие из сформулированной теории, справедливость которых проверяется по специально разработанной методике с помощью специальных экспериментов [3]. Если логические предсказания, вытекающие из построенной теории имеют место в действительности и во всех случаях, то разработанная теория признается верной. Других способов проверки истинности теории не существует. Одновременно с проверкой истинности выявляются границы применимости созданной теории. В случаях, когда теория не подтверждается экспериментальной проверкой, то устанавливаются границы ее применимости, за пределами которых теория должна быть уточнена путем добавления новых или замены введенных ранее гипотез.
4. ПРИМЕНЕНИЕ РАЗРАБОТАННОЙ ТЕОРИИ
К ПРАКТИЧЕСКИМ ЗАДАЧАМ
После того, как разработанная теория выдержала экспериментальную проверку и опыты показали, что она справедлива и применима к поставленным практическим задачам, разрабатываются методики и аппаратура для реализации полученных результатов.
5. СВЯЗЬ МОДЕЛИРОВАНИЯ С ДЕТЕРМИНИРОВАННЫМИ И
СТОХАСТИЧЕСКИМИ МЕТОДАМИ ИЗУЧЕНИЯ ЯВЛЕНИЯ
Выше были приведены ряд примеров, касающихся применяемых в науке моделей из области геометрии, картографии, математики, строительной механики, теории
10-09-2015, 22:26
