А.А. Бондарев, Финансово-экономический факультет, Пятигорский государственный технологический университет
Демократические государства в своем развитии прошли длительный эволюционный путь от авторитарных политических режимов до демократического гражданского общества. Для гражданского общества характерны следующие черты:
- многополярность и сложная структура;
- средняя степень поляризации;
- самоорганизация его членов во имя защиты самых разных интересов и прав;
- демократизация, которая подразумевает снижение управляющих воздействий со стороны центральной власти и передача некоторых функций управления гражданским объединениям, общественным организациям;
- наличие обратной связи, позволяющей центральной власти проводить политический курс, отражающий интересы большинства населения;
- наличие внутренних связей между различными группами населения на основе общности их интересов;
- устойчивое поступательное развитие всей социальной системы в целом, отсутствие значительных колебаний в ее развитии.
Основной характеристикой гражданского общества следует признать его открытость, интернационализм, веротерпимость, наличие большого разнообразия общественных объединений с разнообразным вектором политических и социально-экономических интересов. Именно благодаря открытости и многополюсности гражданское общество является устойчивым социальным образованием, не требующим для поддержания своей устойчивости значительных властных импульсов.
Российское общество еще находится в самом начале эволюционного пути по построению гражданского общества. Современная структура Российского социума является, преимущественно, двухкомпонентной, сильно поляризованной: на одном полюсе олигархическая элита, на другом - остальная часть населения с минимальным прожиточным уровнем.
Взаимодействие двух полюсов такого общества можно характеризовать как силу притяжения, обозначающую общность интересов, или отталкивания, в случае их антагонизма. В первом приближении импульс взаимодействия можно описать следующим уравнением:
![]() (1)
(1)
где, ai – интенсивность вектора интересов группы, характеризующаяся степенью (мерой) воздействия на систему в целом, потенциалом реализации интересов;
qi – удельный вес группы в сообществе;
φij – угол между векторами интересов групп на плоскости политических и социально-экономических интересов, в двухкомпонентной социосистеме находится в пределах от π до π/2.
Антагонизм интересов двух групп создает внутренние напряжения в социуме, делает систему неустойчивой, стремящейся к развалу. Без сильных управляющих воздействий со стороны центральной власти такая система является неустойчивой.
Для прогнозирования динамики такой системы можно применить модели, используемые для описания динамики конфликта[1,с.187-192], основанием этому служит схожесть развития конфликта с типичной картиной неустойчивости, свойственной многим природным и социальным явлениям.
Такое сходство позволяет предложить и вполне адекватную динамическую характеристику конфликтной ситуации — накопленную «напряженность» Y (этот термин удобен применительно именно к конфликтам, хотя фактически речь идет о потенциале). При этом естественно ввести данную характеристику для каждой из участвующих в конфликте сторон, например, Y0 и Y1 , если ограничиться случаем двухстороннего конфликта. Далее, поскольку среди многочисленных факторов наиболее сильными являются лишь те, которые включаются в цепь обратных связей, можно анализировать значительно упрощенный, но сохраняющий это принципиальное положение вариант задачи, когда на изменение величин Y0 и Y1 во времени t аддитивно и линейно влияют обе накопленные напряженности:
![]() , (2)
, (2)
![]() . (3)
. (3)
В системе уравнений (1) и (2), которую можно решать при нулевых начальных условиях, учтено несколько влияющих факторов:
F1,2 — возмущающие факторы, послужившие стартовым толчком;
aii — быстрота «самовозбуждения» каждой из конфликтующих сторон, определяемая внутренними мотивами (i =1, 2);
aik — быстрота внешнего возбуждения стороны (i), связанного с действиями другой стороны (k), или быстрота взаимного влияния сторон друг на друга (в общем случае aik ¹aki; i = 1, 2; k = 1, 2).
Для моделирования состояния двухкомпонентной социосистемы определим следующие значения коэффициентов aii, и aik:
| а11=0,01 | а12=(t-2) |
| а11=0,99 | а22=1 |
Предпосылки для определения таких численных значений коэффициентов aii, и aik следующие:
– интенсивность воздействия каждой группы сообщества на государственную власть, выработку ею управляющих воздействий на систему, пропорциональна финансовому потенциалу этой группы, и может быть определена посредством коэффициентов «Джинни». Для РФ разница в доходах крайних социальных групп составляет более 100;
– как правило, олигархические группы в любой стране имеют возможность влиять на социосистему через политические партии или непосредственно через правительство, эта группа имеет высокую степень организованности и реагирует на изменения системы без опоздания, и наоборот, вторая часть системы – население – имеет низкую степень самоорганизации и самоорганизуется, образует партии, защищающие их интересы, как правило, в кризисных, тяжелых условиях, следовательно, реакция этой системы осуществляется с опозданием, но в динамике этот сегмент социосистемы, самоорганизуясь, увеличивает свой потенциал напряженности. Для целей моделирования примем прямую зависимость между быстротой внешнего возбуждения стороны (0), связанного с действиями другой стороны (1), и временем.
![]()
![]()
Решение системы дифференциальных уравнений в программе Mathcad
![]()
![]()
![]()
![]()
![]()
![]()
показывает, что при принятых значениях коэффициентов aii, и aik, система является неустойчивой (рис. 1).
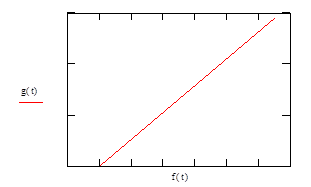
Рис. 1. Фазовый портрет системы
Любое общество не может существовать самостоятельно и всегда испытывает управляющие воздействия со стороны органа управления - государственной власти, оказывающей стабилизирующее воздействие на систему, образуя отрицательные обратные связи в системе. Стабилизирующие обратные связи зависят от величины накопленных напряженностей.
Если управляющее воздействие зависит от Y0 и Y1, то возможны следующие основные варианты.
Вариант 1. Управляющее воздействие центральной власти пропорционально разности напряженностей, накопленных сторонами, и направлены на обе конфликтующие стороны:
![]() . (4)
. (4)
В этом варианте учитываются текущие изменения в конфликте, а усилия ослабляются по мере приближения сторон к равенству сил (паритет силы), тогда вместо уравнений (2) и (3) имеем:
![]() ; (5)
; (5)
![]() . (6)
. (6)
В результате аналитического решения системы дифференциальных уравнений (5 и 6) получаются корни характеристического уравнения, определяющие инкременты неустойчивости.
![]() ; (7)
; (7)
где
m= (a11+a22) ¤2>0; (8)
n=a12a21-a11a22+g[(a22+a21)-(a11+a12)]. (9)
Видно, что при любых значениях параметров aii, aik хотя бы один из корней уравнения (7), например k1, имеет положительную действительную часть (Rek1 > 0). Это означает, что «миротворческое» воздействие (4) недостаточно для стабилизации конфликта. Такой общий вывод применительно к условию (4), где стабилизирующее усилие пропорционально разности накопленных сторонами потенциалов, прямо следует из (5) и (6). Действительно, при Y0 = Y1 скорости роста напряженностей (левые части обоих уравнений) не равны 0, а остаются положительными. Сказанное можно обобщить и на случай нелинейных по Y0,1 стабилизирующих воздействий. Таким образом, управляющие воздействия типа (4), достаточно часто используемые при решении различного рода конфликтов, достичь цели не в состоянии.
Вариант 2. Управляющее воздействие центральной власти на каждую из сторон конфликта пропорционально сумме накопленных сторонами напряженностей:
P0,1 =-g0,1 (Y0 + Y1). (10)
Решение системы дифференциальных уравнений (5) и (6) в программе Mathcad позволяет моделировать поведение системы в случае различных управляющих воздействий со стороны государства на каждую группу социума:
| g0=0,1 | g1=0,5 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Решение системы дифференциальных уравнений представлено на рисунках 2- 9 для различных значений g0 и g1.
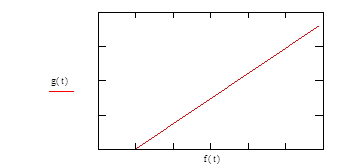
Рис. 2. Фазовый портрет системы при g0=0,1 g1=0,5
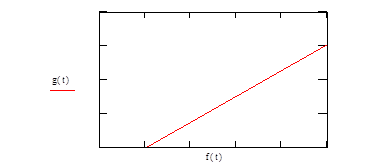
Рис. 3. Фазовый портрет системы при g0=0,5 g1=0,5
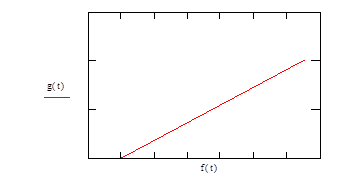
Рис. 4. Фазовый портрет системы при g0=1,0 g1=0,9

Рис. 5. Фазовый портрет системы при g0=0,1 g1=1

Рис. 6. Фазовый портрет системы при g0=0,3 g1=1

Рис. 7. Фазовый портрет системы при g0=0,5 g1=1
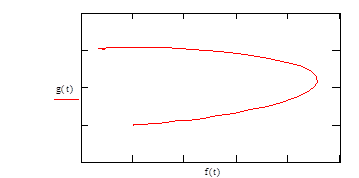
Рис. 8. Фазовый портрет системы при g0=0,9 g1=1
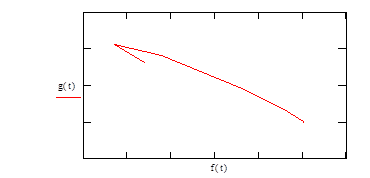
Рис. 9. Фазовый портрет системы при g0=5 g1=5
Результаты моделирования динамики двухкомпонентной социосистемы позволяют сделать следующие выводы:
1. В двухкомпонентной социосистеме для поддержания устойчивости системы требуются сильные управляющие воздействия со стороны государственной власти, что делает ее отнюдь не демократической. Только благодаря сильным управляющим импульсам ее воздействия на систему обеспечивается ее устойчивость, слабая власть не способна удержать систему в равновесии, а сама система разрушается.
2. Управляющее воздействие должно быть направлено на обе полярные социальные группы системы. Равновесие в системе наблюдается первоначально, когда управляющее воздействие со стороны государства на олигархические группы превышает воздействие на группу с низкими доходами, но при этом в развитии общества наблюдаются циклы, и оно достигает устойчивого состояния за длительный временной интервал (рис. 5). При этом появление колебаний в развитии системы обусловлено первой группой населения (низкие доходы). Снижение периода достижения устойчивого состояния достигается усилением управляющего воздействия государственной власти на этот сегмент социосистемы (рис. 6-9). В авторитарном государстве (рис. 9) система достигает высокой степени устойчивости и приходит в состояние равновесия за короткий временной интервал.
Список литературы
1. Либенсон М.Н. Конфликт как объект теории неустойчивости // Синергетика и методы науки / Под ред. М.А. Басина. СПб.: Наука.– 1998.
10-09-2015, 22:47
